EJERCICIOS REFUERZO I soluciones

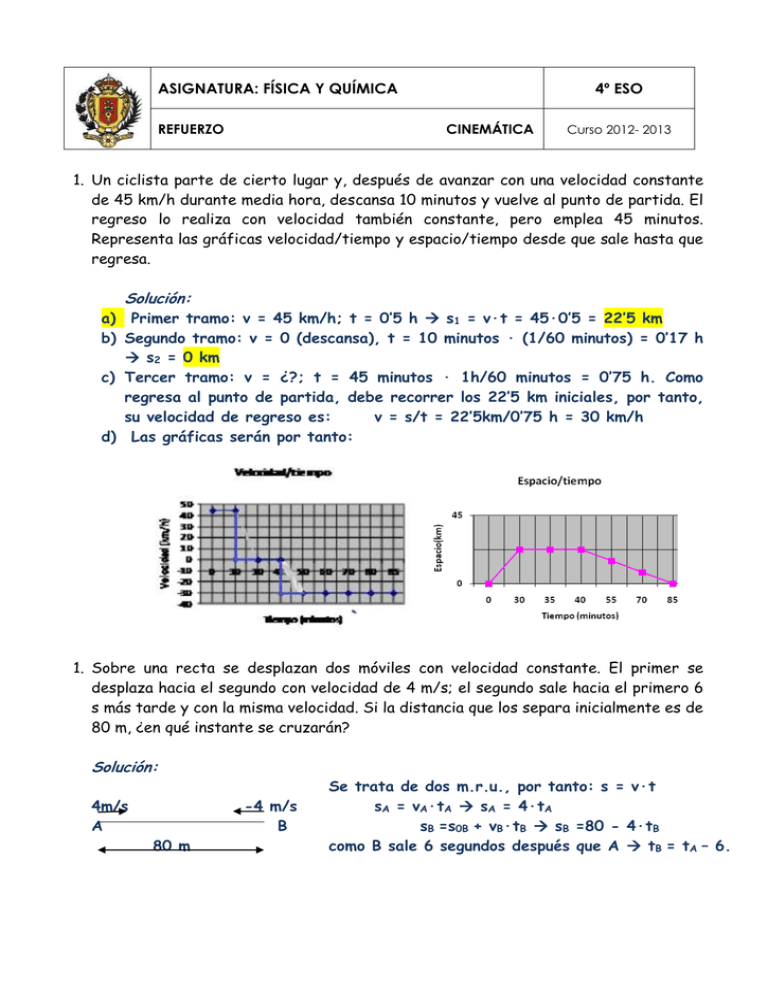
ASIGNATURA: FÍSICA Y QUÍMICA
REFUERZO
4º ESO
CINEMÁTICA
Curso 2012- 2013
1. Un ciclista parte de cierto lugar y, después de avanzar con una velocidad constante
de 45 km/h durante media hora, descansa 10 minutos y vuelve al punto de partida. El
regreso lo realiza con velocidad también constante, pero emplea 45 minutos.
Representa las gráficas velocidad/tiempo y espacio/tiempo desde que sale hasta que
regresa.
Solución:
a) Primer tramo: v = 45 km/h; t = 0’5 h  s1 = v·t = 45·0’5 = 22’5 km
b) Segundo tramo: v = 0 (descansa), t = 10 minutos · (1/60 minutos) = 0’17 h
 s2 = 0 km
c) Tercer tramo: v = ¿?; t = 45 minutos · 1h/60 minutos = 0’75 h. Como
regresa al punto de partida, debe recorrer los 22’5 km iniciales, por tanto,
su velocidad de regreso es:
v = s/t = 22’5km/0’75 h = 30 km/h
d) Las gráficas serán por tanto:
1. Sobre una recta se desplazan dos móviles con velocidad constante. El primer se
desplaza hacia el segundo con velocidad de 4 m/s; el segundo sale hacia el primero 6
s más tarde y con la misma velocidad. Si la distancia que los separa inicialmente es de
80 m, ¿en qué instante se cruzarán?
Solución:
4m/s
A
-4 m/s
B
80 m
Se trata de dos m.r.u., por tanto: s = v·t
sA = vA·tA  sA = 4·tA
sB =s0B + vB·tB  sB =80 - 4·tB
como B sale 6 segundos después que A  tB = tA – 6.
SA=SB  4·tA = 80 - 4·tB  4·tA = 80 - 4·(tA -6)  4·tA + 4·tA - 24 = 80
 8·tA = 104
tA = 13 s
La posición en la que se encuentran es SA=SB  SA = 52m
La distancia recorrida por cada uno será:
SA – S0A = 4·13 - 0 = 52 m
y
SB – S0B = -4·7 = 28 m.
2. Un cuerpo, partiendo del reposo, se mueve con una aceleración constante de 8m/s 2.
¿Cuánto tiempo tarda en recorrer 100 m? ¿cuál será su velocidad en ese instante?
Solución:
Al haber aceleración constante estamos hablando de un m.r.u.a. Sus ecuaciones son:
Vf = v0 + a·t;
s =s0 + v0·t + (a·t2/2)
Los datos son: s0 = 0; v0 = 0; a = 8 m/s2; s = 100 m; t?; v?
Sustituimos los datos en las ecuaciones del movimiento:
V = 0 + 8·t  v = 8t
100 = 0 + 0·t + 8·t2/2 100 = 4t2  25 = t2  t = 5 s

v = 8·5 = 40 m/s
Velocidad (m/s)
3. Interpreta la siguiente gráfica v/t. ¿Cuál es el desplazamiento total recorrido por el
móvil?
60
40
20
0
0
10
20
30
40
tiempo (s)
Solución:
Se trata de una gráfica en tres tramos.
Tramo I: m.r.u.a de aceleración positiva ya que aumenta la velocidad. Su
aceleración es, a = (vf – v0)/t = (50 – 0)/10 = 5 m/s2, y por tanto,
s = 0·10 + 5·102/2 = 250 m
Tramo II: m.r.u. ya que se mantiene constante la velocidad durante 20 s. Si
empezamos a contar desde s0 = 0 y t0=0 s, el espacio recorrido es:
s = v·t = 50·20 = 1000 m
Tramo III: m.r.u.a. de aceleración negativa al disminuir la velocidad.
a = (vf – v0)/t = (0 – 50)/10 = -5 m/s2, y por tanto, empezando a contar desde
s0=0 m y t0=0 s,….
s = 50·10 + (-5)·102/2 = 250 m
Sumando los espacios obtenidos en los tres tramos, obtenemos el espacio total:
s = 250 + 1000 + 250 = 1500 m
______________________________________________________________
También se podría hacer….
Calculando un tramo después de otro y tomando como datos iniciales los datos del
tramo anterior…
Tramo I: m.r.u.a de aceleración positiva ya que aumenta la velocidad. Su
aceleración es, a = (vf – v0)/t = (50 – 0)/10 = 5 m/s2, y por tanto,
s = 0·10 + 5·102/2 = 250 m
Tramo II: m.r.u. ya que se mantiene constante la velocidad durante 20 s.
Si acumuláramos espacio, como la posición correspondería con el espacio recorrido
al ser un movimiento rectilíneo, siempre en el mismo sentido y habiendo partido de
cero, la ecuación sería:
s = s0 + v·t = 250 + 50·(30-10) = 1250 m
Tramo III: m.r.u.a. de aceleración negativa al disminuir la velocidad.
a = (vf – v0)/t = (0 – 50)/10 = -5 m/s2, y por tanto, tomando la s0 = 1250m y
v0= 50m/s…
s = 1250 + 50·10 + [(-5)·(40-30)2/2] = 1500 m
4. Interpretar la siguiente gráfica s/t y calcula la velocidad del móvil en cada tramo.
Solución:
La gráfica representa el movimiento de un cuerpo que tiene lugar en tres tramos.
Tramo I: m.r.u. ya que en 10 s recorre 50 m, por tanto v1 =s/t = 50/10 = 5 m/s.
Tramo II: el cuerpo permanece parado durante 30 s a 50 metros del origen. V2 = 0
Tramo III: m.r.u.; el cuerpo regresa al origen en 5 s.
v3 = s-s0 /t-t0 = (0-50)/(45-40) = -10 m/s
(el sentido de la velocidad es el
contrario al del tramo I, ya que regresa al origen).
5. Desde lo alto de un balcón situado a 6 m del suelo, se suelta una maceta. Una
persona, situada a 5 m del lugar de impacto camina con rapidez constante de 3 m/s
hacia el punto de caída. Despreciando la altura de la persona, ¿le caerá la maceta en
lo alto? En caso negativo, calcula qué rapidez (constante) debería llevar como mínimo
esa persona para evitar que la maceta llegue al suelo.
Solución:
Datos:
VERTICAL h0=6m; v0 = 0
m/s; a = g = -9’8 m/s2
HORIZONTAL v= -3 m/s, s0
= 5m
a) Es una caída libre (m.r.u.a)
de ecuaciones:
vf = v0 + a·t;
h = h0 + v0·t - g·t2/2
El tiempo empleado en bajar se
obtiene con el dato h=0m
h =0 = 6+0– (9,8·t2/2)t=1,1 s
Hay que comprobar cuánto
recorre la persona en ese
tiempo y si coincide con los cinco metros que le separa del lugar donde cae la
maceta, le caerá encima.
Calculamos lo que recorre la persona en 1,1 s
La ecuación será la correspondiente a un m.r.u.
s = s0 + vt  s = 5 – (3∙1,1) = 1,7 m
SOLUCIÓN: La maceta no le cae en la cabeza porque todavía no ha llegado al
punto origen. Le quedan 1,7 m todavía.
¡¡¡UF….MENOS MAL!!!
6. Lanzamos verticalmente y hacia arriba una piedra con una rapidez de 8 m/s. Calcula
qué velocidad llevara cuando pase por la mitad de su altura máxima.
Solución:
Datos: v0 = 8m/s; a = g = -9’8 m/s2
Es un tiro vertical (m.r.u.a) de ecuaciones:
vf = v0 - g·t;
h = h0 + v0·t - g·t2/2
Estará subiendo hasta que se quede sin velocidad (vf = 0). Así podemos calcular la
altura máxima y posteriormente calcular la velocidad cuando pase por la mitad de la
altura.
0 = 8 – 9’8∙t  8 = 9’8∙t  t = 8/9’8 = 0,82 s tarda en subir.
h = 0 + 8·0,82 – 9’8∙0,822/2 = 3,27 m
La mitad de la altura será 1,64 m 
Usando la fórmula: V2 = V02 -2g(h-h0)  V2 =64-2∙9,8∙(1,64 – 0)  V=5,6 m/s
7. Desde lo alto de una azotea soltamos una piedra de 4 kg y justo al mismo tiempo,
otra de 9 kg. ¿Cuál llegará antes al suelo? ¿Cuál lo hará con mayor velocidad?
Llegarán las dos a la vez porque, si no hay rozamiento de ningún tipo, la masa no
influye en la velocidad de caída de un cuerpo.
8. Un vehículo se está moviendo con una rapidez constante de 25 m/s durante 4
minutos. ¿Qué aceleración debería tener un coche para que partiendo del reposo,
consiga recorrer la misma distancia que el vehículo anterior en el mismo tiempo de 4
minutos? ¿Qué rapidez llevará ese coche al final de su recorrido?
Solución:
Datos:
móvil 1  V= 25m/s; t=4min = 240s
Móvil 2  V0=0 m/s; t= 4min = 240s, misma distancia que el anterior
¿a?, ¿rapidez al final del recorrido?
Móvil 1 m.r.u.
Móvil 2  m.r.u.a.
s = s0 + vt; s= 0 + 25∙240 = 6000 m
s =s0 + v0·t + (a·t2/2) ; 6000 =0 + 0 + (a·2402/2) 
a= 0,2 m/s2
v = v0 + at  v = 0 + 0,2∙240 = 50 m/s