Teorema de tales - liceo politécnico c
Anuncio
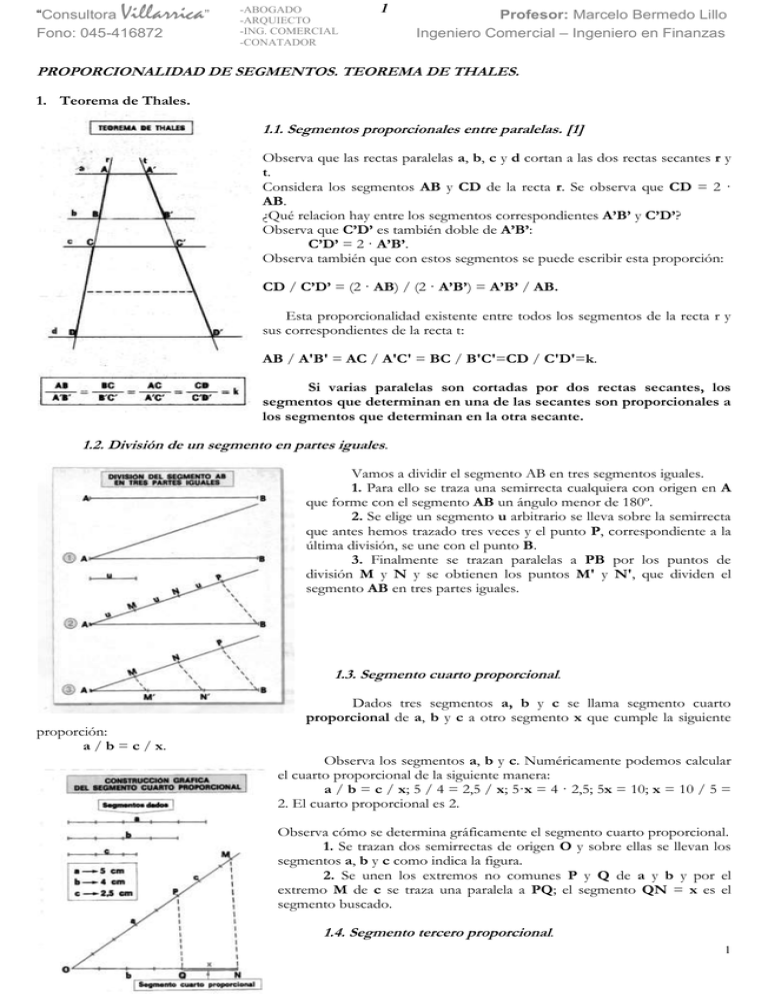
Villarrica” “Consultora Fono: 045-416872 -ABOGADO -ARQUIECTO -ING. COMERCIAL -CONATADOR 1 Profesor: Marcelo Bermedo Lillo Ingeniero Comercial – Ingeniero en Finanzas PROPORCIONALIDAD DE SEGMENTOS. TEOREMA DE THALES. 1. Teorema de Thales. 1.1. Segmentos proporcionales entre paralelas. [1] Observa que las rectas paralelas a, b, c y d cortan a las dos rectas secantes r y t. Considera los segmentos AB y CD de la recta r. Se observa que CD = 2 · AB. ¿Qué relacion hay entre los segmentos correspondientes A’B’ y C’D’? Observa que C’D’ es también doble de A’B’: C’D’ = 2 · A’B’. Observa también que con estos segmentos se puede escribir esta proporción: CD / C’D’ = (2 · AB) / (2 · A’B’) = A’B’ / AB. Esta proporcionalidad existente entre todos los segmentos de la recta r y sus correspondientes de la recta t: AB / A'B' = AC / A'C' = BC / B'C'=CD / C'D'=k. Si varias paralelas son cortadas por dos rectas secantes, los segmentos que determinan en una de las secantes son proporcionales a los segmentos que determinan en la otra secante. 1.2. División de un segmento en partes iguales. Vamos a dividir el segmento AB en tres segmentos iguales. 1. Para ello se traza una semirrecta cualquiera con origen en A que forme con el segmento AB un ángulo menor de 180º. 2. Se elige un segmento u arbitrario se lleva sobre la semirrecta que antes hemos trazado tres veces y el punto P, correspondiente a la última división, se une con el punto B. 3. Finalmente se trazan paralelas a PB por los puntos de división M y N y se obtienen los puntos M' y N', que dividen el segmento AB en tres partes iguales. 1.3. Segmento cuarto proporcional. Dados tres segmentos a, b y c se llama segmento cuarto proporcional de a, b y c a otro segmento x que cumple la siguiente proporción: a / b = c / x. Observa los segmentos a, b y c. Numéricamente podemos calcular el cuarto proporcional de la siguiente manera: a / b = c / x; 5 / 4 = 2,5 / x; 5·x = 4 · 2,5; 5x = 10; x = 10 / 5 = 2. El cuarto proporcional es 2. Observa cómo se determina gráficamente el segmento cuarto proporcional. 1. Se trazan dos semirrectas de origen O y sobre ellas se llevan los segmentos a, b y c como indica la figura. 2. Se unen los extremos no comunes P y Q de a y b y por el extremo M de c se traza una paralela a PQ; el segmento QN = x es el segmento buscado. 1.4. Segmento tercero proporcional. 1 Villarrica” “Consultora Fono: 045-416872 -ABOGADO -ARQUIECTO -ING. COMERCIAL -CONATADOR 2 Profesor: Marcelo Bermedo Lillo Ingeniero Comercial – Ingeniero en Finanzas Dados dos segmentos a y b, se llama segmento tercero proporcional de a y b a otro segmento x que cumple la siguiente proporción: a / b = b / x. Observa los segmentos a y b. Numéricamente podemos calcular el tercero proporcional de la siguiente manera: a / b = b / x; 1 / 2 = 2 / x; x = 4. El tercero proporcional es 4 cm. La construcción gráfica del tercero proporcional se hace como en el caso del cuarto proporcional. 2. Triángulos en posición de Thales. 1. Dibuja en tu cuaderno un triángulo como el triángulo ABC. 2. Traza una paralela A'B' al lado AB. Así se forma un nuevo triángulo CA'B'. Los triángulos CAB y CA'B' se dice que están en posición de Thales o que son triángulos de Thales. lados proporcionales: Veamos que dos triángulos en posición de Thales tienen los ángulos iguales y los Los ángulos de dos triángulos de Thales son iguales. El ángulo C es el mismo para los dos triángulos: A = A' B = B' 3. Los lados de dos triángulos de Thales son proporcionales. Para ver la proporcionalidad de los lados tracemos por el punto B' una paralela B'D al lado CA. Entonces A'B' = AD por ser lados opuestos de un paralelogramo. · Aplicando el teorema de Thales a las paralelas AB A'B', cortadas por CA y CB, resulta la proporción a): a) CA / CA' = CB / CB'. · Aplicando el teorema de Thales a las paralelas AC B'D. cortadas por CB y AB, resulta: AB / A'B' = CB / CB'. y como AD = A'B' resulta la proporción b): las proporciones a) y b) resulta: AB / A'B' = CB / C'B'. De las proporciones a) y b) resulta: CA / CA' = CB / CB' = AB / A'B'. Si dos triángulos están en posición de Thales, entonces sus ángulos son iguales y sus lados correspondientes son proporcionales. 2 Villarrica” “Consultora Fono: 045-416872 -ABOGADO -ARQUIECTO -ING. COMERCIAL -CONATADOR 3 Profesor: Marcelo Bermedo Lillo Ingeniero Comercial – Ingeniero en Finanzas TEOREMA DE THALES 1. En la siguiente figura L1//L2 a) PC = 12 cm., PB = 6cm., BD = 2 cm., AC = ? b) CD = 7 cm., PA = 2 cm., AC = 5 cm., AB = ? c) PC = 9 cm., CD = 6 cm., AB = 5 cm., BD = 1 cm. Determina PA, PB y PD. d) PC = 16 cm., BD = 6 cm., AB = 9 cm., PD = 24 cm. Determina CD y PA. e) PA = 18 cm., AC = 14 cm., PD = 16 cm., BD = ? f) BD = 2 cm., AB = 8 cm., PD = 12 cm., CD = ? g) PC = 20 cm., PA = 15 cm., PD = 40 cm., BD = ? h) PA = 3x, AB = 3x - 2, AC = x + 2, CD = 4x - 1. Determina PC y CD. i) AC = 4,5 cm., PA = 2 cm., PD = 3,6 cm., BD = ? 2. En la siguiente figura L1//L2. a) a = 12 cm., b = 15 cm., c = 20 cm., d = ? b) a = (x - 1) cm., b = 4 cm., c = (2x - 4) cm., d = 7 cm. Determina las medidas de a y c. c) a = 14 cm., c = 10 cm., b + d = 36 cm. Determina la medida de b. d) a = 6 cm., a + c = 14 cm., b + d = 18 cm., d = ? 3 Villarrica” “Consultora Fono: 045-416872 -ABOGADO -ARQUIECTO -ING. COMERCIAL -CONATADOR 4 Profesor: Marcelo Bermedo Lillo Ingeniero Comercial – Ingeniero en Finanzas 3. En la siguiente figura L1//L2. a) BP = 6 cm., CP = 4 cm., CD = 3 cm., AB = ? b) AP = x + 13, BP = 10 cm., PC = 4 cm., PD = x + 4, AP = ? c) BP = 16 cm., CP = 14 cm., DP = 12 cm., AD = ? d) AB = 2 cm., AP = x cm., BP = (y - 3) cm., CP = (y + 2) cm., DP = (x+5) cm., CD = 4 cm. Determina las medidas de BC, AP, BP, CP, DP y AD. 4


