funcionpolinomica
Anuncio
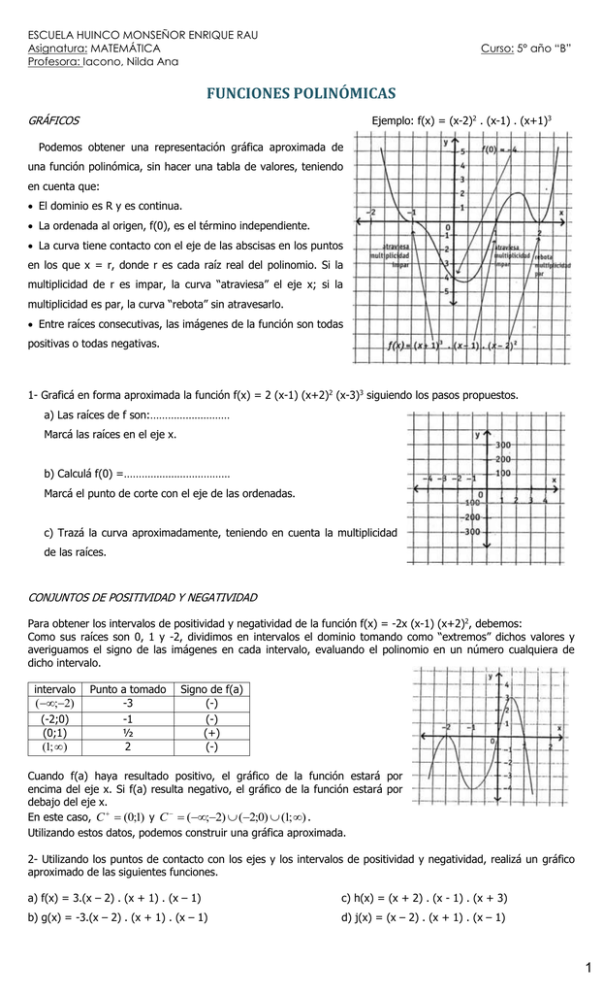
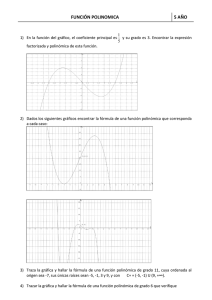
ESCUELA HUINCO MONSEÑOR ENRIQUE RAU Asignatura: MATEMÁTICA Profesora: Iacono, Nilda Ana Curso: 5° año “B” FUNCIONES POLINÓMICAS GRÁFICOS Ejemplo: f(x) = (x-2)2 . (x-1) . (x+1)3 Podemos obtener una representación gráfica aproximada de una función polinómica, sin hacer una tabla de valores, teniendo en cuenta que: El dominio es R y es continua. La ordenada al origen, f(0), es el término independiente. La curva tiene contacto con el eje de las abscisas en los puntos en los que x = r, donde r es cada raíz real del polinomio. Si la multiplicidad de r es impar, la curva “atraviesa” el eje x; si la multiplicidad es par, la curva “rebota” sin atravesarlo. Entre raíces consecutivas, las imágenes de la función son todas positivas o todas negativas. 1- Graficá en forma aproximada la función f(x) = 2 (x-1) (x+2)2 (x-3)3 siguiendo los pasos propuestos. a) Las raíces de f son:……………………… Marcá las raíces en el eje x. b) Calculá f(0) =……………………………… Marcá el punto de corte con el eje de las ordenadas. c) Trazá la curva aproximadamente, teniendo en cuenta la multiplicidad de las raíces. CONJUNTOS DE POSITIVIDAD Y NEGATIVIDAD Para obtener los intervalos de positividad y negatividad de la función f(x) = -2x (x-1) (x+2)2, debemos: Como sus raíces son 0, 1 y -2, dividimos en intervalos el dominio tomando como “extremos” dichos valores y averiguamos el signo de las imágenes en cada intervalo, evaluando el polinomio en un número cualquiera de dicho intervalo. intervalo (;2) (-2;0) (0;1) (1; ) Punto a tomado -3 -1 ½ 2 Signo de f(a) (-) (-) (+) (-) Cuando f(a) haya resultado positivo, el gráfico de la función estará por encima del eje x. Si f(a) resulta negativo, el gráfico de la función estará por debajo del eje x. En este caso, C (0;1) y C (;2) (2;0) (1; ) . Utilizando estos datos, podemos construir una gráfica aproximada. 2- Utilizando los puntos de contacto con los ejes y los intervalos de positividad y negatividad, realizá un gráfico aproximado de las siguientes funciones. a) f(x) = 3.(x – 2) . (x + 1) . (x – 1) c) h(x) = (x + 2) . (x - 1) . (x + 3) b) g(x) = -3.(x – 2) . (x + 1) . (x – 1) d) j(x) = (x – 2) . (x + 1) . (x – 1) 1 RECONSTRUCCIÓN DE FÓRMULAS POLINÓMICAS A PARTIR DE SUS GRÁFICAS 3- La siguiente gráfica corresponde a una función polinómica de grado 3. a) Completá: Sus raíces son: x 1 =……………… x 2 =……………… x 3 =……………… La expresión general de una función cúbica es: f(x) = a (x- x 1 ) (x- x 2 ) (x- x 3 ), en este caso tenemos: f(x) = a (x……) (x……) (x……) (1) b) Otro punto que pertenece a la gráfica es el (0;100). Reemplazando x = 0 y f(0) = 100 en la expresión (1), obtené el valor de a y escribí la fórmula de la función. ………………………………………………….. 4- Se realizaron, en forma aproximada, las siguientes gráficas. Averigua cuál de las fórmulas le corresponde a cada una. l. f(x) = -x . (x+4) . (x-4) ll. f(x) = x . ( x-2) . (x+2) lll. f(x) = x3 – 16x lV. f(x) = -x . (x-2) . (x+2) 5- Hallá la formula de cada una de las funciones que aparecen en los gráficos. a) grado 3 b) grado 4 c) grado 5 Guía práctica 1. es una función polinómica de grado 4, su coeficiente principal es -1 y tiene dos raíces dobles que son y a) Hallar la expresión factorizada y la polinómica de b) Calcular y 2. Dada la función T ( x) x4 7 x3 11x2 7 x a a) Hallar a sabiendo que el gráfico de t corta al eje x en el punto ( 5 ; 0 ) b) Encontrar todos los puntos en los que el gráfico de t corta al eje x 3. Escribir la expresión de una función polinómica que verifique: a) sea de grado 3, con raíces -2, 3 y 4 y f(0)= 12. b) sea de grado 3, x1= - 5 es una raíz simple, x2= - 1 es una raíz doble y f(0)=4 c) sea de grado 4, x1=3 es una raíz doble, x2= - 2 es una raíz doble y f(-1)=2 d) sea de grado 3, cuya única raíz sea x = 2 y corte al eje de ordenadas en el punto ( 0 ; 8 ) 4. Para cada una de las siguientes funciones; hallar sus raíces, el conjunto de positividad y negatividad, la ordenada al origen. Realizar su gráfica aproximada. f ( x) x3 7 x 2 7 x 15 g ( x) x 4 2 x 3 4 x 2 8 x h( x) 2 x3 13x 2 22x 8 i ( x) ( x 2 4).(x3 2 x 2 x) 2