Funciones y puertas básicas
Anuncio
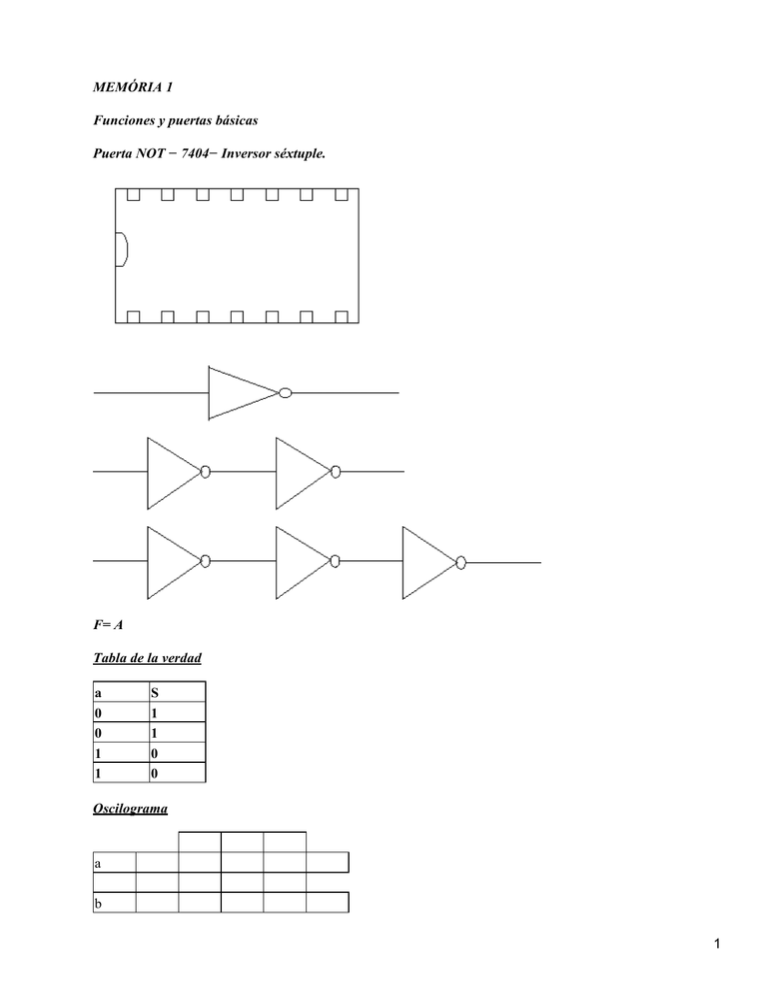
MEMÓRIA 1 Funciones y puertas básicas Puerta NOT − 7404− Inversor séxtuple. F= A Tabla de la verdad a 0 0 1 1 S 1 1 0 0 Oscilograma a b 1 S Conclusión: La puerta Not invierte la función, si entra por la puerta 0 sale 1 y si entra 1 sale o. Puerta AND − 7408 − Cuádruple con 2 entradas y una salida. F= A · B aS b a b S cS d Tabla de la verdad a 0 0 1 1 b 0 1 0 1 S 0 0 0 1 a 0 0 b 0 0 c 0 0 d 0 1 S 0 0 2 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 0 0 0 0 1 1 1 1 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 0 0 1 0 0 0 0 0 0 0 1 Oscilo grama a b S Conclusión La puerta multiplica las 2 entradas, solo el resultado será 1 cuando todas sus entradas sean 1. Puerta OR − 7432 − Cuádruple con 2 entradas y una salida F= A + B a 3 bS a b cS d Tabla de la verdad a 0 0 1 1 b 0 1 0 1 S 0 1 1 1 a 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 b 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 c 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 d 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 S 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 Oscilo grama a b S 4 Conclusión La puerta OR suma a las dos entradas, solo el resultado será 0 cuando las 2 entradas sean 0, si cualquiera de las entradas es 1 el resultado siempre será 1. Puerta NAND − 7400 − Cuádruple con 2 entradas y una salida. F=A · B = A +B a b a b S c d Tabla de la verdad a 0 0 1 1 b 0 1 0 1 S 1 1 1 0 a 0 0 0 0 0 0 b 0 0 0 0 1 1 c 0 0 1 1 0 0 d 0 1 0 1 0 1 S 1 1 1 0 1 1 5 0 0 1 1 1 1 1 1 1 1 1 1 0 0 0 0 1 1 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 1 1 0 1 1 1 0 0 0 0 0 Oscilo grama a b S Conclusión La puerta NAND es la inversa a la puerta And, su resultado en la salida es 1 siempre y cuando en las entradas solo haya uno o dos 1, si en las entradas solo hay 3 o ningún 1 el resultado en la salida siempre es 0. Puertas NOR −7402 − Cuádruple con 2 entradas y una salida. F= A +B +C = A · B · C a bS a 6 b cS d Tabla de la verdad a 0 0 1 1 b 0 1 0 1 S 1 0 0 0 a 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 b 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 c 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 d 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 S 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Oscilograma a b S Conclusión 7 La puerta NOR es la puerta inversa de la OR. Solo el resultado en la salida es 1 cuando todas sus entradas es 0. Puerta XOR − 7486− Cuádruple con 2 entradas y una salida F= A +B = A · B + A · B a bS Tabla de la verdad a 0 0 1 1 b 0 1 0 1 S 0 1 1 0 Oscilograma a b S Conclusión La puerta OR−exclusiva hace que solo la salida sea 1 cuando en la entrada hay un 0 y un 1. Puerta X NOR −7486 + 7404 − F= A +B = A · B + A · B 8 a b Tabla de la verdad a 0 0 1 1 b 0 1 0 1 S 1 0 0 1 Oscilo grama a b S Conclusión La puerta XNOR es la inversa de la XOR Ejercicio 1 Dados 3 interruptores (a, b y c) que gobiernan una lámpara: diseñad un circuito que nos permite encender la lámpara solo en el caso en que estén cerrados 2 interruptores de los tres posibles. ( 1; cerrado, lamp encendida :: 0; abierto, lamp cerrada) a 0 0 0 0 1 1 1 1 b 0 0 1 1 0 0 1 1 c 0 1 0 1 0 1 0 1 S 0 0 0 1 0 1 1 0 F= (abc) + (abc) + (abc) ab En este circuito se utilizan puertas la siguientes puertas: 9 • NOT (7404) • AND (7411) *al no tener el 7411 se han utikizado 2 (7408) • Or (7432) Ejercicio 2 a 0 0 1 1 b 0 1 0 1 S 0 1 1 0 Conclusión Este circuito es el mismo que el de una puerta XOR. Todo el circuito esta compuesto por puertas NAND. 10
