Ejercicio nº 1.- Ejercicio nº 2.-

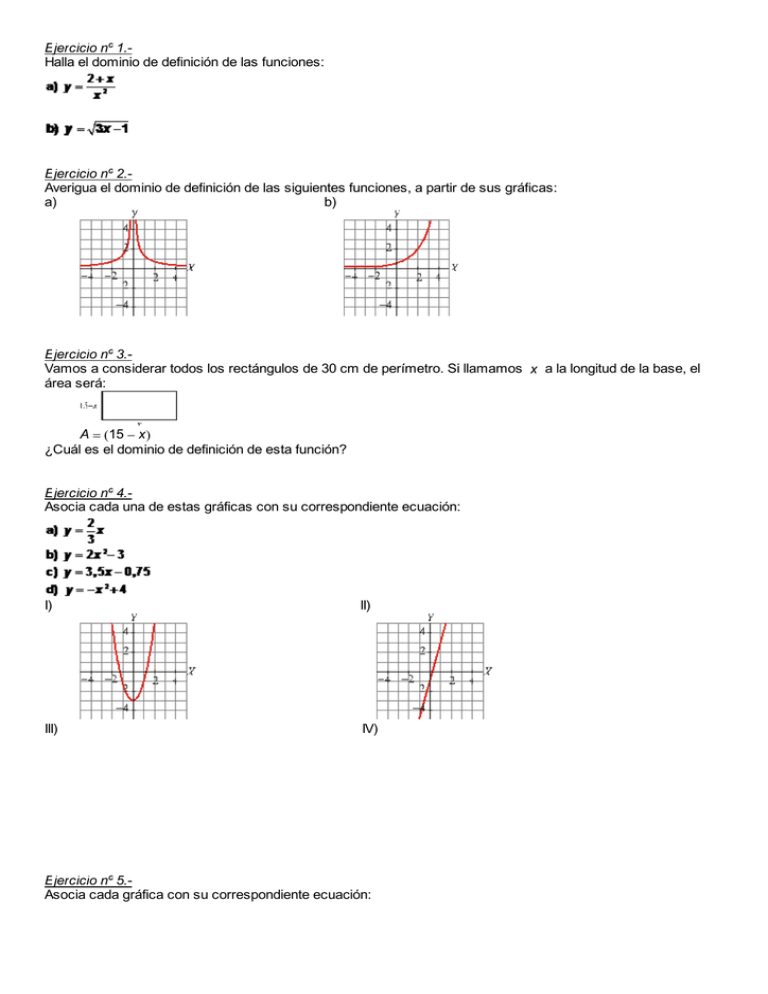
Ejercicio nº 1.Halla el dominio de definición de las funciones:
Ejercicio nº 2.Averigua el dominio de definición de las siguientes funciones, a partir de sus gráficas:
a)
b)
Ejercicio nº 3.Vamos a considerar todos los rectángulos de 30 cm de perímetro. Si llamamos x a la longitud de la base, el
área será:
A  15  x
¿Cuál es el dominio de definición de esta función?
Ejercicio nº 4.Asocia cada una de estas gráficas con su correspondiente ecuación:
I)
II)
III)
IV)
Ejercicio nº 5.Asocia cada gráfica con su correspondiente ecuación:
I)
II)
III)
IV)
Ejercicio nº 6.-
Ejercicio nº 7.Sabiendo que 15 C (grados centígrados) equivalen a 59 F (grados Fahrenheit), y que
30 C son 86 F, averigua cuántos grados centígrados son 70 F. ¿Y 92 F?
Ejercicio nº 8.Representa gráficamente la siguiente función:
Ejercicio nº 9.Representa la siguiente función:
Ejercicio nº 10.siguiente:
Ejercicio nº 11.Ponemos al fuego un cazo con hielo cuya temperatura es de 20 C. En 10 minutos se descongela y se
mantiene a 0 C otros 10 minutos más. Un cuarto de hora más tarde llega a alcanzar 100 C.
a Representa la función que describe este fenómeno y halla su expresión analítica.
b ¿Cuál es el dominio y el recorrido de la función?
Funciones y gráficas
Para practicar
1. Considera la función que a cada nº le
asigna su cuadrado menos 1. Escribe su
expresión analítica y calcula la imagen
de -1, 1 y 2. Calcula también los cortes
con los ejes.
7. Estudia la simetría de las funciones:
a) f(x)= x3+2x
c) f(x)= 2 x2 + 1 d) f(x)=
2. Considera la función que a cada nº le
asigna su mitad más 3. Escribe su
expresión analítica y calcula la imagen
de -1, 1 y 3. Calcula también los cortes
con los ejes.
3. Considera la función que a cada nº le
asigna su doble menos 5. Escribe su
expresión analítica y calcula la imagen
de -2, -1 y 1. Calcula también los cortes
con los ejes.
b) f(x)=
e) f(x)=
4x2 + 1
2x
x2 − 3
5x2
x +1
x −1
f) f(x)= x4-3x2-3
8. En cada caso la gráfica representa un
tramo o periodo de una función
periódica, representa otros tramos,
indica el periodo y calcula la imagen del
punto de abscisa que se indica:
a) f(-2)
4. Calcula
el dominio de las siguientes
funciones:
a) f(x)=-2x2+5x-6
b) f(x)=
2x
2x − 4
b) f(-3)
c) f(x)= − 4x2 + 12
4x2 + 20
d) f(x)=
3
e) f(x)=
2x − 4
5. Estudia la continuidad de las siguientes
c) f(-1)
funciones:
a) f(x)=
x −2
x −3
b) f(x)=
−x
x+3
6. Estudia la continuidad de las siguientes
funciones en los puntos que se indica:
⎧ x+2 x ≤1
en x=1
a) f(x)= ⎨
⎩− x + 2 x > 1
9. Calcula las TVM de las funciones de la
gráfica en los intervalos [0,4] y [2,4].
a)
b)
⎧2x + 2 x ≤ 0
en x=0
⎩x+2 x > 0
b) f(x)= ⎨
⎧ − x + 3 x ≤ −1
en x=-1
x > −1
⎩ 4
c) f(x)= ⎨
⎧ − x + 3 x ≤ −1
en x=-1
x > −1
⎩ 4
d) f(x)= ⎨
MATEMÁTICAS B „
141
Funciones y gráficas
10. El
gráfico muestra cómo varía la
gasolina que hay en mi coche durante
un viaje de 520 km por una autovía.
a) ¿Cuánta gasolina había al cabo de
240 km?. En el depósito caben 40 litros,
¿cuándo estaba lleno más de medio
depósito?.
b) ¿En cuántas gasolineras paré?, ¿en
qué gasolinera eché más gasolina?. Si
no hubiera parado, ¿dónde me habría
quedado sin gasolina?
c) ¿Cuánta gasolina usé en los primeros
200 km?. ¿Cuánta en todo el viaje?.
¿Cuánta gasolina gasta el coche cada
100 km en esta autovía?.
11. María y Jorge son dos personas más o
menos típicas. En la gráfica puedes
comparar como ha crecido su peso en
sus primeros 20 años
12. El gráfico da el espacio recorrido por
dos coches que realizan un mismo
trayecto.
a) ¿Cuál es la distancia recorrida?. ¿Si
el primer coche salió a las 10:00, a qué
hora salió el 2º?. ¿Cuánto le costó a
cada uno hacer el recorrido?
b) ¿Cuánto tiempo y dónde estuvo
parado cada coche?. ¿En qué km
adelantó el 2º al 1º?, ¿y el 1º al 2º?.
c) ¿Qué velocidad media llevaron en el
trayecto total?, ¿en qué tramo la
velocidad de cada coche fue mayor?.
13. Las gráficas siguientes
corresponden a
las funciones I y II.
I) f(x)=x3-6x2+9x
II) f(x)= −
x2 + 1
x
Calcula en cada una:
a) El dominio.
a) ¿Cuánto pesaba Jorge a los 8 años?,
¿y María a los 12?. ¿Cuándo superó
Jorge los 45 kg?.
b) Los puntos de corte con los ejes.
c) Los valores de x para los que la
función es positiva y negativa.
b) ¿A qué edad pesaban los dos igual?.
¿Cuándo pesaba Jorge más que María?,
¿y María más que Jorge?
d) Los intervalos
decrecimiento.
c) ¿Cuál fue el promedio en kg/año de
aumento de peso de ambos entre los 11
y los 15 años?. ¿En qué periodo creció
cada uno más rápidamente?
f) ¿Cuántos puntos de inflexión tienen?.
142
„ MATEMÁTICAS B
de
crecimiento
y
e) Los máximos y mínimos.
g) Los intervalos
convexidad.
de
concavidad
y
Definición de derivada
Ejercicio nº 1.Halla la tasa de variación media de la siguiente función en el intervalo 1, 2] e indica
f x   2 x 2  3 x
Ejercicio nº 2.-
Calcula,utilizando la definición de deriv ada, f´ (1) para la función f x  
x 1
.
3
Ejercicio nº 3.-
Utilizando la definición de deriv ada,calcula f´(x) para la función f x  
x 1
.
3
Ejercicio nº 4.Halla la función derivada de:
a) f x   3 x 4  2 x  5
b) f x   e x
Ejercicio nº 5.Halla la función derivada de las siguientes funciones:
x2  2
2x  1
b) f x   xe x
a) f x  
Ejercicio nº 6.Calcula la derivada de la función:
f x   4 x 3  1
Ejercicio nº 7.Consideramos la función:
f x  
x2 1
2
Halla la tasa de variación media en el intervalo [0, 2] e indica si f(x) crece o decrece en ese intervalo.
Ejercicio nº 8.-
a) Calcula la tasa de v ariaciónmedia de la función f x  
3
en el interv alo [ 3,1]
x
b) A la vista del resultado obtenido en el apartado anterior, ¿crece o decrece la función
en dicho intervalo?
1
Ejercicio nº 9.Calcula la tasa de variación media de esta función, f(x), en los intervalos siguientes
e indica si la función crece o decrece en cada uno de dichos intervalos:
a) 1, 0
b)
 1, 2
Ejercicio nº 10.-
Utilizando la definición de deriv ada, calcula f´ (1), siendo f x  
3x  1
.
2
Ejercicio nº 11.-
Aplicando la definición de deriv ada,calcula f'  1 , siendo f x  
2
.
x
Ejercicio nº 12.-
Calcula,utilizando la definición de deriv ada, f´ (1) para la función f x  
x 1
.
3
Ejercicio nº 13.-
Halla la deriv ada de la función f x   x  1 en x  2, aplicando la definición de deriv ada.
2
Ejercicio nº 14.Halla la derivada de la siguiente función en x = 1, aplicando la definición de derivada:
f x   x 2  1
Ejercicio nº 15.-
Halla la deriv adade la función f x   2 x 2, aplicandola definición de deriv ada.
Ejercicio nº 16.-
Utilizando la definición de deriv ada,calcula f´(x) para la función f x  
x 1
.
3
Ejercicio nº 17.-
Halla f´(x), aplicandola definiciónde deriv ada, siendo f (x)  x 2  1.
2
Ejercicio nº 18.-
Aplicando la definición de deriv adacalcula f' x  , siendo f x  
1
.
x
Cálculo de derivadas
Ejercicio nº 19.Halla la función derivada de:
a) f x   4 x 3  3 x 2  2
b) f x   tg x
Ejercicio nº 20.Calcula la función derivada de:
a) f x   2 x 3  x 2  1
b) f x   lnx
Ejercicio nº 21.Halla la derivada de:
a) f x   x 3  3 x 2 
b) f x   cos x
1
5
Ejercicio nº 22.Halla la función derivada de las siguientes funciones:
a) f x   2 x 5 
b) f x   sen x
x
3
Ejercicio nº 23.Halla la función derivada de:
a) f x   3 x 4  2 x  5
b) f x   e x
Ejercicio nº 24.Calcula f´(x) en cada caso:
a) f x  
3x 2
2x  3
b) f x   3 x  sen x
3
Ejercicio nº 25.Halla la función derivada de:
1 x 2
x 3
b) f x   x ln x
a) f x  
Ejercicio nº 26.Calcula la derivada de las funciones siguientes:
3x  1
x2 2
b) f x   x 2 sen x
a) f x  
Ejercicio nº 27.Halla la función derivada de las siguientes funciones:
x2  2
2x  1
b) f x   xe x
a) f x  
Ejercicio nº 28.Halla la derivada de las siguientes funciones:
a) f x  
2
x
3x  1
b) f x  
ex
x 
Ejercicio nº 29.Halla la derivada de las siguientes funciones:
a) f x  
2
x
3x  1
b) f x  
ex
x 
Ejercicio nº 30.Calcula la derivada de la función:
f x   4 x 3  1
Ejercicio nº 31.Halla la función derivada de:

f x   3 x 2  x

4
4
Ejercicio nº 32.Halla f´(x) para la función:
f x   e 4 x
3
2 x
Ejercicio nº 33.Calcula la función derivada de:
 x 1 
f x   sen 

 2x  3 
Aplicaciones de la derivada
Ejercicio nº 34.Escribe la ecuación de la recta tangente a la curva y = 2x  3x que tenga pendiente 7.
2
Ejercicio nº 35.-
Halla la ecuaciónde la recta tangente a la curv a y 
x que sea paralela a la recta y 
1
x 1
4
Ejercicio nº36.Halla la ecuación de la recta tangente a la curva y = x + 2x 1 en el punto de abscisa x = 1.
2
Ejercicio nº 37.Escribe la ecuación de la recta tangente a la curva y = x 2x en el punto de abscisa x  2.
3
Ejercicio nº 38.2
Halla la ecuación de la recta de pendiente 7 que es tangente a la curva y = 3x + x -1.
Ejercicio nº 39.Averigua los puntos de tangente horizontal de la función:
f x  
3  x2
x 2
Ejercicio nº 40.Halla y representa gráficamente los puntos singulares de la función:
f x   x 4  2x 2
5
Ejercicio nº 41.Determina los puntos de tangente horizontal de la función:
x3
x 2
f x  
Ejercicio nº 42.Halla los puntos de tangente horizontal de la siguiente función y, con ayuda de las ramas infinitas,
decide si son máximos o mínimos:
f x   x 3  6 x 2  15x
Ejercicio nº 43.Halla y representa gráficamente los máximos y mínimos de la función:
y  x 3  3x 2  9x  1
Ejercicio nº 44.Dada la función:
f x   2x 3
determina los tramos en los que la función crece y en los que decrece.
Ejercicio nº 45.Estudia el crecimiento y el decrecimiento de la siguiente función:
f x   3 x 2  2 x  1
Ejercicio nº 46.Estudia dónde crece y dónde decrece la función:
f x   3  12x  3 x 2
Ejercicio nº 47.Estudia el crecimiento y el decrecimiento de la función:
f x  
x 2  3x  1
2
Ejercicio nº 48.Halla los intervalos de crecimiento y de decrecimiento de la función:
f  x   x  2 
2
6
Ejercicios de Cálculo de Probabilidades
Ejercicio nº 1.De una bolsa que tiene 10 bolas numeradas del 0 al 9, se extrae una bola al azar.
a ¿Cuál es el espacio muestral?
b Describe los sucesos:
A  "Mayor que 6"
B  "No obtener 6"
C  "Menor que 6"
escribiendo todos sus elementos.
c Halla los sucesos A  B , A  B y B'  A'.
Ejercicio nº 2.Extraemos dos cartas de una baraja española y vemos de qué palo son.
a ¿Cuál es el espacio muestral? ¿Cuántos elementos tiene?
b Describe los sucesos:
A  "Las cartas son de distinto palo"
B  "Al menos una carta es de oros"
C  "Ninguna de las cartas es de espadas"
escribiendo todos sus elementos.
c Halla los sucesos B  C y B'  C.
Ejercicio nº 3.En una urna hay 15 bolas numeradas de 2 al 16. Extraemos una bola al azar y observamos el número que
tiene.
a Describe los sucesos:
A  "Obtener par"
C  "Obtener primo"
B  "Obtener impar"
D  "Obtener impar menor que 9"
escribiendo todos sus elementos.
b ¿Qué relación hay entre A y B? ¿Y entre C y D?
c ¿Cuál es el suceso A  B? ¿y C  D?
Ejercicio nº 4.Consideramos el experimento que consiste en lanzar tres monedas al aire.
a ¿Cuál es el espacio muestral? ¿Cuántos elementos tiene?
b Describe los sucesos:
A  "Obtener dos caras y una cruz"
B  "Obtener al menos dos caras"
1
C  "Obtener al menos una cruz"
escribiendo todos sus elementos.
c Halla los sucesos B  C y C'
Ejercicio nº 5.Lanzamos dos dados sobre la mesa y anotamos los dos números obtenidos.
a ¿Cuántos elementos tiene el espacio muestral?
b Describe los sucesos:
A  "Obtener al menos un cinco"
B  "La suma de los resultados es menor que 4"
C  "La suma de los resultados es igual a 7"
escribiendo todos sus elementos
c Halla los sucesos A  B y B  C'.
Ejercicio nº 6.A partir de esta probabilidades:
P[A  B']  0,8
P[A']  0,5
P[A  B]  0,2
Calcula P[B] y P[A  B].
Ejercicio nº 7.Sabiendo que:
P[A  B]  0,2
P[B']  0,7
P[A  B']  0,5
Calcula P[A  B] y P[A].
Ejercicio nº 8.De dos sucesos, A y B, sabemos que:
P[A'  B']  0
Calcula P[B]
P[A'  B']  0,5
y
P[A']  0,4
P[A  B].
Ejercicio nº 9.Sean A y B los sucesos tales que:
P[A]  0,4
P[A'  B]  0,4
P[A  B]  0,1
Calcula P[A  B] y P[B].
2
Ejercicio nº 10.Teniendo en cuenta que:
P[A  B]  0,9
P[B']  0,4
P[A  B]  0,3
Halla P[A] y P[A'  B].
Ejercicio nº 11.Si A y B son dos sucesos tales que:
P[A]  0,4
P[B / A]  0,25
P[B']  0,75
a ¿Son A y B independientes?
b Calcula P[A  B] y P[A  B].
Ejercicio nº 12.Teniendo en cuenta que A y B son dos sucesos tales que:
P[A']  0,5
P[A  B]  0,12
P[A  B]  0,82
a ¿Son independientes A y B?
b Calcula P[B' / A].
Ejercicio nº 13.Sean A y B dos sucesos de un espacio de probabilidad tales que:
P[A']  0,6
P[B]  0,3
P[A'  B']  0,9
a ¿Son independientes A y B?
b Calcula P[A' / B].
Ejercicio nº 14.De dos sucesos A y B sabemos que:
P[A']  0,48
P[A  B]  0,82
P[B]  0,42
a ¿Son A y B independientes?
b ¿Cuánto vale P[A / B]?
Ejercicio nº 15.Sabiendo que:
P[A]  0,5
P[B']  0,6
P[A'  B']  0,25
a ¿Son A y B sucesos independientes?
b Calcula P[A  B] y P[A / B].
3
Ejercicio nº 16.Tenemos para enviar tres cartas con sus tres sobres correspondientes. Si metemos al zar cada carta en uno
de los sobres, ¿cuál es la probabilidad de que al menos una de las cartas vaya en el sobre que le
corresponde?
Ejercicio nº 17.a) Dos personas eligen al azar, cada una de ellas, un número del 1 al 5. ¿Cuál es la probabilidad de que las
dos elijan el mismo número?
b) Si son tres personas las que eligen al azar, cada una de ellas, un número del 1 al 5, ¿cuál es la
probabilidad de que las tres elijan el mismo número?
Ejercicio nº 18.Extraemos dos cartas de una baraja española (de cuarenta cartas). Calcula la probabilidad de que sean:
a) Las dos de oros.
b) Una de copas u otra de oros.
c) Al menos una de oros.
d) La primera de copas y la segunda de oro.
Ejercicio nº 19.Dos personas eligen al azar, cada una de ellas, un número del 0 al 9. ¿Cuál es la probabilidad de que las dos
personas no piensen el mismo número?
Ejercicio nº 20.En unas oposiciones, el temario consta de 85 temas. Se eligen tres temas al azar de entre los 85. Si un
opositor sabe 35 de los 85 temas, ¿cuál es la probabilidad de que sepa al menos uno de los tres temas?
Ejercicio nº 21.En una cadena de televisión se hizo una encuesta a 2 500 personas para saber la audiencia de un debate y
de una película que se emitieron en horas distintas: 2 100 vieron la película, 1 500 vieron el debate y 350 no
vieron ninguno de los dos programas. Si elegimos al azar a uno de los encuestados:
a ¿Cuál es la probabilidad de que viera la película y el debate?
b ¿Cuál es la probabilidad de que viera la película, sabiendo que no vio el debate?
c Sabiendo que vio la película, ¿cuál es la probabilidad de que viera el debate?
Ejercicio nº 22.En un viaje organizado por Europa para 120 personas, 48 de los que van saben hablar inglés, 36 saben
hablar francés, y 12 de ellos hablan los dos idiomas.
Escogemos uno de los viajeros al azar.
a ¿Cuál es la probabilidad de que hable alguno de los dos idiomas?
b ¿Cuál es la probabilidad de que hable francés, sabiendo que habla inglés?
c ¿Cuál es la probabilidad de que solo hable francés?
Ejercicio nº 23.En un viaje organizado por Europa para 120 personas, 48 de los que van saben hablar inglés, 36 saben
hablar francés, y 12 de ellos hablan los dos idiomas.
Escogemos uno de los viajeros al azar.
4
a ¿Cuál es la probabilidad de que hable alguno de los dos idiomas?
b ¿Cuál es la probabilidad de que hable francés, sabiendo que habla inglés?
c ¿Cuál es la probabilidad de que solo hable francés?
Ejercicio nº 24.En un pueblo hay 100 jóvenes; 40 de los chicos y 35 de las chicas juegan al tenis. El total de chicas en el
pueblo es de 45. Si elegimos un joven de esa localidad al azar:
a ¿Cuál es la probabilidad de que sea chico?
b Si sabemos que juega al tenis, ¿cuál es la probabilidad de que sea chica?
c ¿Cuál es la probabilidad de que sea un chico que no juegue al tenis?
Ejercicio nº 25.En una clase de 30 alumnos hay 18 que han aprobado matemáticas, 16 que han aprobado inglés y 6 que no
han aprobado ninguna de las dos.
Elegimos al azar un alumno de esa clase:
a ¿Cuál es la probabilidad de que haya aprobado inglés y matemáticas?
b Sabiendo que ha aprobado matemáticas, ¿cuál es la probabilidad de que haya aprobado inglés?
c ¿Son independientes los sucesos "Aprobar matemáticas" y "Aprobar inglés"?
Ejercicio nº 26.Una bola bolsa, A, contiene 3 bolas rojas y 5 verdes. Otra bolsa, B, contiene 6 bolas rojas y 4 verdes.
Lanzamos un dado: si sale un uno, extraemos una bola de la bolsa A; y si no sale un uno, la extraemos de
B.
a ¿Cuál es la probabilidad de obtener una bola roja?
b Sabiendo que salió roja, ¿cuál es la probabilidad de que fuera de A?
Ejercicio nº 27.Tenemos dos bolsas, A y B. En la bolsa A hay 3 bolas blancas y 7 rojas. En la bolsa B hay 6 bolas
blancas y 2.rojas. Sacamos una bola de A y la pasamos a B. Después extraemos una bola de B.
a ¿Cuál es la probabilidad de que la bola extraída de B sea blanca?
b ¿Cuál es la probabilidad de que las dos bolas sean blancas?
Ejercicio nº 28.Una urna, A, contiene 7 bolas numeradas del 1 al 7. En otra urna, B, hay 5 bolas numeradas del 1 al 5.
Lanzamos una moneda equilibrada, de forma que, si sale cara, extraemos una bola de la urna A y, si sale
cruz, la extraemos de B.
a ¿Cuál es la probabilidad de obtener un número par?
b Sabiendo que salió un número par, ¿cuál es la probabilidad de que fuera de la urna A?
Ejercicio nº 29.El 1% de la población de un determinado lugar padece una enfermedad. Para detectar esta enfermedad se
realiza una prueba de diagnóstico. Esta prueba da positiva en el 97% de los pacientes que padecen la
enfermedad; en el 98% de los individuos que no la padecen da negativa. Si elegimos al azar un individuo de
esa población:
a ¿Cuál es la probabilidad de que el individuo dé positivo y padezca la enfermedad?
5
b Si sabemos que ha dado positiva, ¿cuál es la probabilidad de que padezca la enfermedad?
Ejercicio nº 30.Tenemos dos urnas: la primera tiene 3 bolas rojas, 3 blancas y 4 negras; la segunda tiene 4 bolas rojas, 3
blancas y 1 negra. Elegimos una urna al azar y extraemos una bola.
a ¿Cuál es la probabilidad de que la bola extraída sea blanca?
b Sabiendo que la bola extraída fue blanca, ¿cuál es la probabilidad de que fuera de la primera urna?
6