Problemas de Genética resueltos

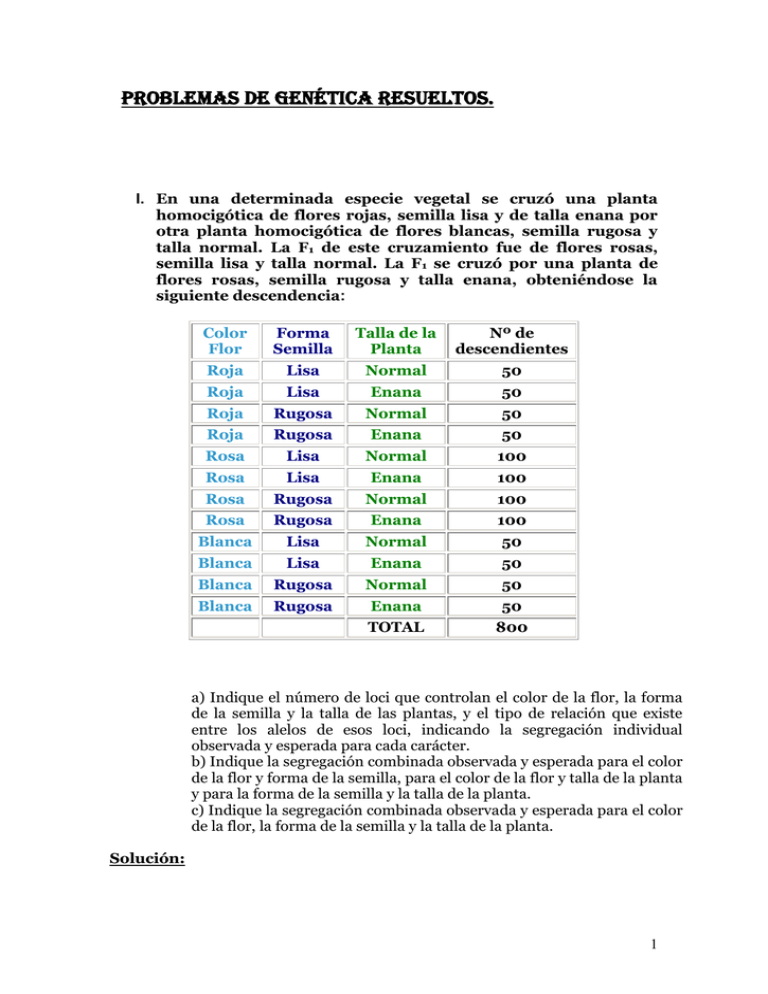
Problemas de Genética resueltos.
I. En una determinada especie vegetal se cruzó una planta
homocigótica de flores rojas, semilla lisa y de talla enana por
otra planta homocigótica de flores blancas, semilla rugosa y
talla normal. La F1 de este cruzamiento fue de flores rosas,
semilla lisa y talla normal. La F1 se cruzó por una planta de
flores rosas, semilla rugosa y talla enana, obteniéndose la
siguiente descendencia:
Color
Flor
Forma
Semilla
Talla de la
Planta
Nº de
descendientes
Roja
Lisa
Normal
50
Roja
Lisa
Enana
50
Roja
Rugosa
Normal
50
Roja
Rugosa
Enana
50
Rosa
Lisa
Normal
100
Rosa
Lisa
Enana
100
Rosa
Rugosa
Normal
100
Rosa
Rugosa
Enana
100
Blanca
Lisa
Normal
50
Blanca
Lisa
Enana
50
Blanca
Rugosa
Normal
50
Blanca
Rugosa
Enana
50
TOTAL
800
a) Indique el número de loci que controlan el color de la flor, la forma
de la semilla y la talla de las plantas, y el tipo de relación que existe
entre los alelos de esos loci, indicando la segregación individual
observada y esperada para cada carácter.
b) Indique la segregación combinada observada y esperada para el color
de la flor y forma de la semilla, para el color de la flor y talla de la planta
y para la forma de la semilla y la talla de la planta.
c) Indique la segregación combinada observada y esperada para el color
de la flor, la forma de la semilla y la talla de la planta.
Solución:
1
a) Indique el número de loci que controlan el color de la flor, la forma de la
semilla y la talla de las plantas, y el tipo de relación que existe entre los alelos de
esos loci, indicando la segregación individual observada y esperada para cada
carácter.
Empezaremos planteando la hipótesis más sencilla, que consiste en
que cada carácter está controlado por un solo gen con dos alelos, y
comprobaremos que dicha hipótesis es coherente con los datos expuestos
en el enunciado.
Color de la flor: Llamemos R al alelo que produce flores color
rojo y r al alelo que produce flores color blanco. Según se dice en el
enunciado, los parentales del primer cruzamiento son homocigotos, uno
de ellos con flores rojas (RR) y el otro con flores blancas (rr) La F1 de
este cruzamiento estará compuesta de individuos híbridos (Rr) que
resultan ser todos de color rosa, lo cual sugiere que el gen presenta
dominancia intermedia (acción génica aditiva) Las plantas híbridas
de la F1 se cruzan por plantas de flores rosas que, si nuestra hipótesis es
cierta, deben ser heterocigotas (Rr) y se espera que la segregación
genotípica de la descendencia sea: 1 RR : 2 Rr : 1 rr, y la fenotípica
1 Rojo : 2 Rosa : 1 Blanco. Si en la tabla anterior agrupamos los
individuos con el mismo fenotipo para este carácter observaremos:
Plantas de flores rojas  50  50  50  50  200



Plantas de flores rosas  100  100  100  100  400 
Plantas de flores blancas  50  50  50  50  200 


200 RR : 400 Rr : 200 rr  1RR : 2 Rr : 1rr
Forma de la semilla: Llamemos L al alelo que produce semillas
lisas y l al alelo que produce semillas rugosas. Según se dice en el
enunciado los parentales del primer cruzamiento son homocigotos, uno
de ellos con semillas lisas (LL) y el otro con semillas rugosas (ll) La F1 de
este cruzamiento estará compuesta de individuos híbridos (Ll) que
resultan ser todos de semilla lisa, lo cual sugiere que el gen presenta
dominancia completa del alelo L (L > l) Las plantas híbridas de la F1
se cruzan por plantas de semilla rugosa que, si nuestra hipótesis es cierta,
deben ser homocigotas recesivas (ll), es decir, se realiza un cruzamiento
prueba y se espera que la segregación genotípica de la descendencia sea:
1 Ll : 1 ll, y la fenotípica 1 Lisa : 1 Rugosa. Si en la tabla anterior
agrupamos los individuos con el mismo fenotipo para este carácter
observaremos:
Plantas de semilla lisa  50  50  100  100  50  50  400



Plantas de semilla rugosa  50  50  100  100  50  50  400 
400 Ll : 400 ll  1Ll : 1ll
2
Talla de la planta: Llamemos N al alelo que produce plantas de
talla normal y n al alelo que produce plantas enanas. Según se dice en el
enunciado los parentales del primer cruzamiento son homocigotos, uno
de ellos de talla normal (NN) y el otro de talla enana (nn) La F1 de este
cruzamiento estará compuesta de individuos híbridos (Nn) que resultan
ser todos de talla normal, lo cual sugiere que el gen presenta
dominancia completa del alelo N (N > n) Las plantas híbridas de la
F1 se cruzan por plantas de talla enana que, si nuestra hipótesis es cierta,
deben ser homocigotas recesivas (nn), es decir, se realiza un cruzamiento
prueba y se espera que la segregación genotípica de la descendencia sea:
1 Nn : 1 nn, y la fenotípica 1 Normal : 1 Enana . Si en la tabla anterior
agrupamos los individuos con el mismo fenotipo para este carácter
observaremos:
Plantas de talla normal  50  50  100  100  50  50  400 


Plantas enanas  50  50  100  100  50  50  400

400 Nn : 400 nn  1Nn : 1nn
En resumen, cada uno de los caracteres está controlado por un gen
con dos alelos. En el caso de los caracteres “forma de la semilla” y “talla
de la planta”, existe un alelo que dominante (el que determina semilla
lisa, L, y el que determina plantas de talla normal, N) y un alelo recesivo
(el que determina semilla rugosa, l, y el que determina plantas enanas, n)
En el caso del carácter “color de la flor” ambos alelos presentan
dominancia intermedia, siendo Rojo y Blanco los fenotipos de los
individuos homocigotos y Rosa el del heterocigoto.
c) Indique la segregación combinada observada y esperada para el color de la
flor y forma de la semilla, para el color de la flor y talla de la planta y para la
forma de la semilla y la talla de la planta.
La segregación combinada de cada pareja de caracteres depende de
que los caracteres segreguen independientemente o no. Como en la
pregunta anterior plantearemos la hipótesis más simple, que es la
hipótesis de segregación independiente, y observaremos que dicha
hipótesis es coherente con los datos expuestos en el enunciado.
Color de la flor y forma de la semilla
El carácter “color de la flor” está controlado por el gen R , r que
presenta dominancia intermedia y el carácter “forma de la semilla” está
controlado por el gen L , l que presenta dominancia completa del alelo L .
El cruce realizado es un cruzamiento entre híbridos, para el primer
carácter, que producirá una segregación fenotípica
1 Rojo : 2 Rosa : 1 Blanco, y un cruzamiento prueba para el segundo,
que producirá una segregación fenotípica 1 Lisa : 1 Rugosa. La
3
segregación combinada esperada para ambos caracteres se obtiene
mediante el producto cartesiano de ambas segregaciones:
1Rojo Lisa
1Rojo Rugosa

2 Rosa Lisa
1Rojo : 2 Rosa : 1Blanco  x 1Lisa : 1Rugosa  
2 Rosa Rugosa
1Blanca Lisa

1Blanca Rugosa
Para obtener la segregación combinada observada para ambos
caracteres sumamos, en la tabla anterior, las frecuencias de aquellas
plantas hijas que comparten un mismo fenotipo para esta pareja de
caracteres:
50  50 =
50  50 =
100  100
100  100
50  50 =
50  50 =

1Rojo Lisa

1Rojo Rugosa
100 Rojo Rugosa 


2 Rosa Lisa
= 200 Rosa Lisa
  
= 200 Rosa Rugosa 
2 Rosa Rugosa

1Blanca Lisa
100 Blanca Lisa


100 Blanca Rugosa 
1Blanca Rugosa
100 Rojo Lisa
Como se puede apreciar, ambas segregaciones son la misma.
Color de la flor y talla de la planta
El carácter “color de la flor” está controlado por el gen R , r que
presenta dominancia intermedia y el carácter “talla de la planta” está
controlado por el gen N , n que presenta dominancia completa del alelo
N.
El cruce realizado es un cruzamiento entre híbridos, para el primer
carácter, que producirá una segregación fenotípica
1Rojo: 2 Rosa: 1 Blanco, y un cruzamiento prueba para el segundo,
que producirá una segregación fenotípica
1 Talla normal: 1 Talla enana. La segregación combinada esperada
para ambos caracteres se obtiene mediante el producto cartesiano de
ambas segregaciones:
1Rojo Normal
1Rojo Enana

2 Rosa Normal
1Rojo : 2 Rosa : 1Blanco  x 1Normal : 1Enana  
2 Rosa Enana
1Blanca Normal

1Blanca Enana
4
Para obtener la segregación combinada observada para ambos
caracteres sumamos, en la tabla anterior, las frecuencias de aquellas
plantas hijas que comparten un mismo fenotipo para esta pareja de
caracteres:
50  50 =
50  50 =
100  100
100  100
50  50 =
50  50 =

1Rojo Normal

1Rojo Enana
100 Rojo Enana 


2 Rosa Norm al
= 200 Rosa Normal 
  
= 200 Rosa Enana 
2 Rosa Enana
1Blanca Normal
100 Blanca Normal 


100 Blanca Enana 
1Blanca Enana
100 Rojo Normal
Como se puede apreciar, ambas segregaciones son la misma.
Forma de la semilla talla de la planta
El carácter “forma de la semilla” está controlado por el gen L , l que
presenta dominancia completa del alelo L y el carácter “talla de la planta”
está controlado por el gen N , n que presenta dominancia completa del
alelo N.
El cruce realizado es un cruzamiento prueba para ambos caracteres,
que producirá segregación fenotípica 1 Lisa : 1 Rugosa para el primer
carácter y 1 Talla normal : 1 Talla enana para el segundo. La
segregación combinada esperada para ambos caracteres se obtiene
mediante el producto cartesiano de ambas segregaciones:
1Lisa Normal
1Lisa Enana
1Lisa
:
1Rugosa
x
1Normal
:
1Enana

 
 
1Rugosa Normal
1Rugosa Enana
Para obtener la segregación combinada observada para ambos
caracteres sumamos, en la tabla anterior, las frecuencias de aquellas
plantas hijas que comparten un misma fenotipo para esta pareja de
caracteres:
50  100  50
50  100  50
50  100  50
50  100  50
=
=
=
=
200 Lisa Normal

1Lisa Normal

1Lisa Enana
200 Lisa Enana


  
200 Rugosa Normal
1Rugosa Normal
1Rugosa Enana
200 Rugosa Enana 
Como se puede apreciar, ambas segregaciones son la misma.
d) Indique la segregación combinada observada y esperada para el color de la
flor, la forma de la semilla y la talla de la planta.
5
Una vez que ya sabemos, por los apartados anteriores, que cada uno
de los caracteres estudiados está controlado genéticamente por un gen
con dos alelos, que segregan independientemente por parejas,
obtendremos la segregación combinada esperada para los tres caracteres
hallando el producto cartesiano de las tres segregaciones individuales:
1Rojo Lisa Normal
1Rojo Lisa Enana

1Rojo Rugosa Normal

1Rojo Rugosa Enana
2 Rosa Lisa Normal

2 Rosa Lisa Enana
1Rojo : 2 Rosa :1Blanco  x 1Lisa :1Rugosa  x 1Normal :1Enana  
2 Rosa Rugosa Normal
2 Rosa Rugosa Enana

1Blanco Lisa Normal
1Blanco Lisa Enana

1Blanco Rugosa Normal
1Blanco Rugosa Enana

Esta segregación esperada es la misma que la observada, tal como se
recoge en la tabla del enunciado:



1Rojo Rugosa Normal 

1Rojo Rugosa Enana 

2 Rosa Lisa Normal

2 Rosa Lisa Enana


2 Rosa Rugosa Normal 
2 Rosa Rugosa Enana 

1Blanco Lisa Normal


1Blanco Lisa Enana

1Blanco Rugosa Normal
1Blanco Rugosa Enana 
1Rojo Lisa Normal
1Rojo Lisa Enana

50 Rojo Lisa Normal
50 Rojo Lisa Enana

50 Rojo Rugosa Normal

50 Rojo Rugosa Enana
100 Rosa Lisa Normal

100 Rosa Lisa Enana

100 Rosa Rugosa Normal
100 Rosa Rugosa Enana

50 Blanco Lisa Normal
50 Blanco Lisa Enana

50 Blanco Rugosa Normal
50 Blanco Rugosa Enana

II. Si se autofecunda un individuo heterocigótico en cinco loci
independientes (AaBbCcDdEe):
6
a) ¿Cuántos gametos genéticamente distintos puede producir ?.
b) ¿Qué número de genotipos diferentes aparecerán en la
descendencia?.
c) ¿Cuál es la frecuencia esperada de individuos heterocigóticos en tres
loci y homocigóticos dominantes en los dos restantes?.
d) ¿Cuál es la frecuencia esperada de descendientes AaBbCcDDEE ?.
Solución:
a) ¿Cuántos gametos genéticamente distintos puede producir?.
Un individuo pentaheterocigoto, heterocigoto en cinco loci, tiene
cinco parejas de alelos en su genotipo. Como los genes son
independientes, la formación de los gametos es equivalente al muestreo
aleatorio de cinco alelos, uno de cada pareja, con iguales probabilidades
para todos ellos. Así pues, el número de gametos genéticamente distintos
se puede calcular como las variaciones con repetición de dos alelos
tomados de cinco en cinco:
R
V2,5
 25  32
b) ¿Qué número de genotipos diferentes aparecerán en la descendencia?.
La descendencia de un heterocigoto, obtenida por autofecundación,
se ajusta, para cada gen X,x a la segregación genotípica mendeliana:
1 XX : 2 Xx : 1 xx. Como los cinco genes son independientes, al
reproducirse por autofecundación, un pentaheterocigoto produce una
descendencia en la que el número de genotipos diferentes se puede
calcular observando que el proceso formación de los genotipos es
equivalente al muestreo aleatorio de cinco genotipos, uno para cada gen,
habiendo tres posibilidades diferentes en cada caso. Así pues, el número
de genotipos diferentes se puede calcular como las variaciones con
repetición de tres posibles genotipos en un gen, tomados de cinco en
cinco:
R
V3,5
 35  243
c) ¿Cuál es la frecuencia esperada de individuos heterocigóticos en tres loci y
homocigóticos dominantes en los dos restantes?.
En esta descendencia obtenida por autofecundación del
pentaheterocigoto, si la evaluación del genotipo total que nos interesa
depende del número de veces que aparece entre los cinco genes cada
posible genotipo en un locus (homocigoto mayúscula, heterocigoto y
homocigoto minúscula), podemos calcular frecuencias genotípicas
utilizando la función de probabilidad de la distribución multinomial:
7
 d loci homocigotos XX 
d
h
r

  n  1   1   1 
Probabilidad  h loci heterocigotos Xx   
     
 r loci homocigotos xx   d h r   4   2   4 


donde  n = Nº de loci
Que, en el caso de la pregunta formulada en el enunciado, resulta ser:
 2 loci homocigotos XX 
2
3
0
5
 1   1   1 
5!
1 1 10
5

 
Probabilidad  3 loci heterocigotos Xx   
  

      
2! 3! 0! 16 8 128 64
 0 loci homocigotos xx   2 3 0   4   2   4 


d) ¿Cuál es la frecuencia esperada de descendientes AaBbCcDDEE?.
En este caso, la evaluación del genotipo que nos interesa incluye la
descripción detallada del genotipo de cada uno de los cinco genes, así que
para el cálculo de frecuencias multiplicaremos las probabilidades de los
genotipos en cada locus:
P  AaBbCcDDEE   P  Aa   P Bb   P  Cc   P DD   P EE  
1 1 1 1 1
1
    
2 2 2 4 4 128
Este resultado es el mismo que obtuvimos anteriormente, salvo que
ahora hemos suprimido el número combinatorio porque estamos
interesados en una descripción detallada del genotipo.
 2 loci homocigotos XX 


P  3 loci heterocigotos Xx 
2
3
0
 0 loci homocigotos xx 
   1   1   1   1  1 1  1
P  AaBbCcDDEE   






5
128


 4   2   4  16 8


2
3
0


III. La incapacidad para detectar el sabor amargo de la
feniltiocarbamida (PTC) en la especie humana se debe a un gen
recesivo frente al alelo que permite detectar el sabor amargo
de la PTC. En un matrimonio en el que ambos padres son
8
heterocigóticos para este locus se han tenido 6 descendientes.
Determine las probabilidades de las siguientes descendencias
o familias:
a) Cuatro descendientes detectan el sabor amargo de la PTC y dos no lo
detectan.
b) Todos distinguen el sabor amargo.
c) Al menos uno de los descendientes detecta el sabor amargo de la
PTC.
d) Los cuatro descendientes mayores distinguen el sabor amargo y los
dos más jóvenes no lo detectan.
e) Sólo uno de los descendientes detecta el sabor amargo de la PTC.
f) Si los cinco mayores detectan el sabor amargo que el sexto no lo
distinga.
Solución:
El cruce de dos heterocigotos para un locus con dominancia
completa produce una descendencia con una segregación:
3 dominante: 1 recesivo. La variable X que cuenta el número de hijos
de un determinado fenotipo (dominante o recesivo) entre n hijos tiene
distribución binomial siendo sus parámetros: n, el número de hijos, y p,
la probabilidad del éxito; el valor de p será 0,75 si llamamos éxito al
hecho de tener fenotipo dominante ó 0,25, si llamamos éxito al hecho de
tener fenotipo recesivo. Así pues, las frecuencias de las distintas familias
con x hijos de fenotipo dominante y n-x de fenotipo recesivo se calculan
utilizando la expresión general:
x
n 3   1 
P X  x      
 x 4   4 
n x
x
En nuestro problema
 6 3   1 
    
 x  4   4 
6 x
Cuando estemos interesados en familias con una secuencia concreta
simplemente tendremos que omitir el número combinatorio.
Determine la probabilidades de que en una familias
a) Determine la probabilidad de que, en una familia, cuatro descendientes
detecten el sabor amargo de la PTC y dos no lo detecten.
4
 6 3   1 
P  X  4       
 4 4   4 
64
 15 
81 1 1.215


256 16 4.096
b) Determine la probabilidad de que, en una familia, todos distingan el sabor
amargo.
9
6
6 3   1 
P  X  6       
6 4   4 
6 6
 1
729
729
1 
4096
4.096
c) Determine la probabilidad de que, en una familia, al menos uno de los
descendientes detecte el sabor amargo de la PTC.
X
 6  3   1 
P  X  1        
X 1  X   4   4 
6
6 X
X
 6  3   1 
 1       
X 0  X   4   4 
1
6 X

 6   3 0  1 6 0  6   3 1  1  6 1 
 1                
 1   4   4  
 0   4   4 
1
3
1 
18 

 1
 1  1 1
 6 

1




4.096
4 1.024 

 4.096 4.096 
 1
19
4.077

4.096 4.096
d) Determine la probabilidad de que, en una familia, los cuatro descendientes
mayores distingan el sabor amargo y los dos más jóvenes no lo detecten.
4
2
81 1
81
 3   1
P  4D  2d      


256 16 4.096
4 4
e) Determine la probabilidad de que, en una familia, sólo uno de los
descendientes detecte el sabor amargo de la PTC.
1
6 3   1 
P  X  1      
 1  4   4 
6 1
 6
3
1
18


4 1024 4.096
f) Determine la probabilidad de que, en una familia, si los cinco mayores
detectan el sabor amargo, el sexto no lo distinga.
La forma más sencilla de resolver este caso consiste en darse cuenta
de que, no importa lo que haya pasado con los demás hermanos, la
probabilidad de que cada uno de ellos sea insensible a la PTC es 1/4.
No obstante, podríamos decir que, de una forma general, esta
frecuencia se calcula como la probabilidad de que el sexto hermano no
detecte el sabor de la PTC, condicionada a que los hermanos mayores
sean todos sensibles a la PTC.
10
5
6 5
 3  1
243 1

4 4
P  5D  1d 5D 
P  5D  1d  
1
P  5D  1d 5D  

   5  55  1.024 4 
243
4
P  X  5 n  5
P  X  5 n  5  5   3   1 
1
1
    
1.024
5 4   4 
IV. Se cruzó una liebre homocigota de pelo blanco por otra
homocigota de pelo castaño, obteniéndose en la primera
generación filial (F1) varios descendientes de pelo blanco. Los
individuos de la F1 se cruzaron entre si obteniéndose una F2
formada por 244 liebres blancas, 24 liebres de pelo castaño y
68 liebres negras.
a) ¿Podría estar controlada la coloración del pelaje en estas liebres por
un solo locus?
b) Explique estos resultados.
Solución:
a) ¿Podría estar controlada la coloración del pelaje en estas liebres por un solo
locus?
Hasta la generación F1, inclusive, no hay ningún motivo para
suponer que el control genético de este carácter sea algo más complejo
que un locus con dos alelos y dominancia completa, dado que se trata de
un cruce de dos homocigotos que produce una descendencia uniforme.
No obstante, en la F2 aparece un fenotipo nuevo, que no se mostraba
ni en los parentales ni en los híbridos de la F1. Así pues, en este caso,
parece que el control genético debe implicar a más de un locus, por
ejemplo a dos, en el caso más sencillo, y a algún tipo de interacción entre
genes no alélicos, es decir, como mínimo, debe tratarse de dos genes con
interacción epistática.
b) Explique estos resultados.
Existen varios tipos posibles de epistasia en un sistema de dos loci
que se distinguen por la segregación de la F2:
11
Modelo de epistasia Segregación
Simple dominante
12 : 3 : 1
Simple recesiva
9:3:4
Doble dominante
15 : 1
Doble recesiva
9:7
Doble dominante-recesiva
13 : 3
Nuestro caso debe de ser alguno de los dos primeros puesto que la
segregación de la F2 incluye 3 fenotipos.
Para saber cuál es la segregación de nuestra descendencia problema,
nos fijamos en la proporción entre el fenotipo más frecuente (blanco) y el
más infrecuente (castaño) y observamos que hay 12,2 ratones blancos por
cada ratón castaño. Esto nos sugiere que se trata de una epistasia simple
dominante. Podemos fijarnos, además, que la proporción de ratones
negros a ratones castaños es de 2,8 a 1, muy similar a la 3 : 1 que
esperaríamos en este caso.
Ahora que tenemos una hipótesis concreta podemos realizar una
prueba de ajuste para comprobarla. Para ello calculamos T, el número
total de ratones en la descendencia F2 y las frecuencias esperadas de cada
fenotipo.
T  122  10  28  160
12
 160  120
16
1
E  Castaño  
 160  10
16
3
E Negro  
 160  30
16
E Blanco  
y calculamos el valor del estadístico de contraste:
2
2
2
2
3
Oi  Ei 
122  120 
12  10 
28  30 




2
2  



 0,167
Ei
120
10
30
i1
La  tiene dos grados de libertad porque, para calcular las
frecuencias esperadas, el único parámetro que hemos tenido que calcular
a partir de las frecuencias observadas es T.
2
Si hacemos la prueba con un nivel de significación del 5% el valor
22; 0,95  5,99
crítico será:
, que es mayor que nuestro valor; por tanto,
concluimos que la segregación observada se ajusta a la de una epistasia
simple dominante.
(Esta prueba se puede realizar, alternativamente, en la página de
chi-cuadrado incluida en el curso)
12
Si llamamos A,a y B,b a los dos loci implicados, siendo A y B los
alelos dominantes (A > a y B > b) y A el alelo epistático sobre el locus B,b,
la correspondencia entre genotipos y fenotipos es la siguiente:
Fenotipo
12 Blanco AABB
3 Negro
1 Castaño
AABb
Genotipo
Aabb AaBB
aaBB aaBb
aabb
AaBb
Aabb
V. En una determinada especie de roedores se cruzaron
individuos de capa color negro por otros de capa blanca. Los
individuos de la F1 tenían capa negra. Cruzando los individuos
de la F1 se originó una F2 formada por 82 animales negros y 62
de color blanco. Un cruzamiento posterior entre dos
individuos blancos de esta F2 dio lugar, en cuatro camadas
sucesivas, a 45 animales negros.
a) Proponga una hipótesis que explique estos resultados.
b) ¿Qué genotipo deben tener los dos individuos de capa blanca de la F 2 para
que todos sus descendientes sean de capa negra?
c) Suponga cruzamos dos hijos del cruce anterior, ¿Cuál sería la probabilidad
de que originara una descendencia formada por 9 animales negros y 3
blancos?
Solución:
a) Proponga una hipótesis que explique estos resultados.
Hasta la generación F1, inclusive, no hay ningún motivo para
suponer que el control genético de este carácter sea algo más complejo
que un locus con dos alelos y dominancia completa del alelo causante del
color negro, dado que podría tratarse de un cruce de dos homocigotos
que produce una descendencia uniforme.
En la F2 aparece una segregación 82 : 62 que, en ningún caso, puede
considerarse coherente con la segregación mendeliana 3 : 1 que debería
aparecer en la descendencia de un monohíbrido (Esta prueba se puede
realizar en la página de chi-cuadrado incluida en el curso)
Así pues, en este caso, parece que el control genético debe implicar a
más de un locus, por ejemplo a dos, y a algún tipo de interacción entre
genes no alélicos, es decir, como mínimo, debe tratarse de dos genes con
interacción epistática.
Recordemos los posibles modelos de epistasia que producen
segregaciones de la F2 con sólo dos clases fenotípicas:
Modelo de epistasia
Doble dominante
Doble recesiva
Segregación
15 : 1
9:7
13
Doble dominante-recesiva
13 : 3
El único modelo verosímil para una segregación observada 82 : 62
es una epistasia doble recesiva. El paso siguiente es realizar una prueba
de ajuste para comprobar nuestra hipótesis. Para ello calculamos T, el
número total de animales en la descendencia F2 y las frecuencias
esperadas de cada fenotipo.
T  82  62  144
9
 144  81
16
7
E Blanco  
 160  63
16
E Negro  
y calculamos el valor del estadístico de contraste:
2
 Oi  E i 
i1
Ei
 
2
1
2
 82  81

81
2
 62  63 

63
2
 0,028
La  tiene un grado de libertad porque, para calcular las
frecuencias esperadas, hemos tenido que calcular T a partir de las
frecuencias observadas.
2
Si hacemos la prueba con un nivel de significación del 5% el valor
2  3,84
crítico será: 1; 0,95
; que es mayor que nuestro valor; por tanto,
concluimos que la segregación observada se ajusta a la de una epistasia
doble recesiva.
(Esta prueba se puede realizar, alternativamente, en la página de
chi-cuadrado incluida en el curso)
Si llamamos A,a y B,b a los dos loci implicados, siendo A y B los
alelos dominantes (A > a y B > b), la correspondencia entre genotipos y
fenotipos es la siguiente:
Fenotipo
Genotipo
9 Negro
AABB AABb AaBB AaBb
7 Blanco AAbb Aabb aaBB aaBb aabb
b) ¿Qué genotipo deben tener los dos individuos de capa blanca de la F2 para
que todos sus descendientes sean de capa negra?
Vamos a suponer, tal como insinúa el enunciado del problema, que
estos padres de capa blanca sólo pueden producir hijos de capa negra.
Para que esto ocurra, es necesario que los padres sean homocigotos
recesivos para alguno de los dos loci y que los hijos reciban con
seguridad, procedente de uno u otro de sus padres, un alelo dominante
para cada uno de sus loci. Para que ocurran ambas cosas
14
simultáneamente es necesario que ambos padres sean homocigotos para
ambos genes y que, si uno de ellos es homocigoto en un locus para el alelo
recesivo, el otro padre sea homocigoto para el alelo dominante.
Por tanto el cruce descrito debe ser:
AAbb x aaBB
AaBb
c) Suponga cruzamos dos hijos del cruce anterior, ¿Cuál sería la probabilidad de
que originara una descendencia formada por 9 animales negros y 3 blancos?
Los hijos del cruce anterior son diheterocigotos, como los individuos
de la F1. Por tanto, la segregación de la descendencia será la misma que la
de la F2, es decir, 9 : 7 .
La segregación propuesta en la pregunta es 9 : 3 ó 3 : 1 que sería la
segregación de un monohíbrido. La probabilidad de que una epistasia
doble recesiva simule una segregación monohíbrida, sobre una muestra
de tamaño 12, podemos calcularla utilizando la función de probabilidad
binomial; consideraremos una variable x que cuenta el número de
individuos de un determinado fenotipo entre 12 pruebas (n) y tomando
como probabilidad del éxito (p) el valor 9/16; si consideramos éxito a
tener la capa blanca.
 12   9   7 
12!  99 73 
4
P  X  9        
 12   220  4,72  10  0,1039
9
16
16
9!
3!
16
    


9
3
VI. Los conejos albinos tienen un precio mucho más elevado en las
tiendas de animales. El albinismo en los conejos y en otras
especies animales se debe a la presencia en homocigosis de un
gen recesivo. Un criador de conejos lleva a cabo un
cruzamiento entre dos conejos heterocigóticos de color gris
para tratar de conseguir gazapos de color blanco.
¿Cuántos descendientes debe tener en este cruzamiento si desea
obtener al menos un gazapo blanco con una fiabilidad de 0,995?.
Solución:
¿Cuántos descendientes deben tener en este cruzamiento si desea obtener al
menos un gazapo blanco con una fiabilidad de 0,995?
15
Consideraremos la variable X, que cuenta el número de conejos
blancos en la descendencia de dos heterocigotos; ésta variable tiene
distribución binomial, con parámetros: n, el tamaño familiar, y p, la
probabilidad de ser homocigoto recesivo en la descendencia de dos
heterocigotos, que vale 1/4.
La probabilidad de tener x conejos blancos en una descendencia de
tamaño n será, por tanto:
n 1 
P  X  x     
 x 4 
x
n x
 1
1 4 


En concreto, la probabilidad de no tener ninguno (x = 0) se puede
0
n 0
n
n
n 1   1 
 1  1
P  X  0      1    1 1 1     1  
 4  4
0 4   4 
calcular como:
y, la de tener al menos uno como la probabilidad del suceso contrario:
n
 1
P  X  0   1  P  X  0   1  1  
 4
Como consecuencia, si queremos tener una fiabilidad de 0,995 de
obtener al menos un gazapos blanco, la probabilidad de este suceso debe
ser igual a 0,995:
n
n
1
1


P  X  0   1   1    0,995   1    1  0,995  0,005
 4
 4
log  0,005 
1

 n log  1    log  0,005   n 
 18,42 19
1

 4
log  1  
 4
Es decir, que si obtenemos 19 gazapos (o más) tendremos una
fiabilidad (confianza) de obtener al menos uno de color blanco de 0,995
(o mayor)
16
VII. La siguiente genealogía corresponde a una familia en la que se
manifiesta un carácter infrecuente en la especie humana:
Suponiendo que se trate de un carácter controlado por un sólo gen
con dos alelos y que el fenotipo anormal tenga penetrancia completa,
responda a las siguientes cuestiones:
a) ¿El alelo que produce el fenotipo es dominante o recesivo?
b) ¿Se trata de un gen autosómico?, o bien, ¿está situado en el
segmento diferencial del cromosoma X? ¿O en el del cromosoma Y?
c) Indique el genotipo más probable de todos los individuos de la
genealogía.
d) De las 6 niñas indicadas como individuos problema en la
genealogía, ¿cuántas se espera que manifiesten el fenotipo anormal?
Solución:
a) ¿El alelo que produce el fenotipo es dominante o recesivo?
El alelo que produce la enfermedad es claramente recesivo.
La característica diagnóstica más clara de los caracteres producidos
por alelos dominantes con penetrancia completa es que, salvo mutación,
todos los individuos afectados son hijos de afectados, puesto que el gen se
muestra en el fenotipo en todas las generaciones.
En cambio, si el alelo es recesivo, podremos observar afectados hijos
de parejas de individuos no afectados, en los que el gen ha quedado
encubierto por su alelo dominante en el fenotipo de los padres. En la
descendencia del primer cruce de la generación 1, cruce que se realiza
entre dos individuos no afectados, aparecen dos hombres afectados, lo
cual demuestra claramente que se trata de un alelo recesivo.
b) ¿Se trata de un gen autosómico?, o bien, ¿está situado en el segmento
diferencial del cromosoma X? ¿O en el del cromosoma Y?
17
Para empezar, no puede tratarse de un gen del segmento diferencial
del cromosoma Y porque, si así fuera, no habría mujeres afectadas.
De las otras dos posibilidades, sólo la de que se trate de un gen
situado en el segmento diferencial del cromosoma X puede descartarse, a
veces. En concreto, si se trata de un gen situado en el segmento
diferencial del cromosoma X, en el caso de una familia en la que la madre
fuese afectada y el padre no, se produciría herencia cruzada, es decir, los
hijos serían todos afectados, como su madre, y las hijas serían todas
sanas, como su padre. Si en una genealogía existe una familia en la que la
madre es afectada y el padre no, y no existe herencia cruzada, bien
porque aparecen hijos sanos, bien porque aparecen hijas afectadas,
entonces pensaremos que se trata de un locus autosómico. No obstante,
si existe herencia cruzada sólo podremos decir que lo observado es
coherente con un caso de herencia ligada al sexo y que esta posibilidad es
tanto más probable cuanto más grande sea la familia en cuestión.
Por otra parte, el resto de la genealogía aportará información valiosa
a contrastar. Por ejemplo, si sospechamos que se trata de un gen situado
en el segmento diferencial del cromosoma X, debemos confirmar que en
la genealogía, si existe alguna familia que incluya hijos afectados y padres
sanos, los hijos afectados sólo pueden ser varones, pues todas las hijas
heredarán de su padre un alelo normal y, por tanto serán, como mínimo,
heterocigotas, es decir, sanas.
En nuestra genealogía existe una familia que presenta herencia
cruzada, cuyos padres son los dos últimos individuos de la generación 2.
Además, la familia a la que aludíamos en el apartado anterior, y de la que
dedujimos que se trataba de un alelo recesivo, tiene padres sanos y los
hijos afectados son todos varones. Ambas cosas podrían ocurrir en el caso
de un locus autosómico pero, si se tratara de un locus ligado al sexo, la
probabilidad de estas dos familias sería 4546 veces mayor.
  4   3 2  1 2  3  4 
P Locus autosomico            
 2 4   4   4  


  4   3 4  4   1 4 
       
 4 4   4 4  


 9x81   81 
5
 6
  65536   8,25 x 10
65536



  4   1 2  1 2 
6
P Locus ligado al sexo           1 
 2 2   2  
16


Así pues, concluimos que debe tratarse de un gen situado sobre el
segmento diferencial del cromosoma X.
18
c) Indica el genotipo más probable de todos los individuos de la genealogía.
Si llamamos A y a al alelo dominante y recesivo, respectivamente, el
genotipo más probable de cada individuo será:
d) De las 6 niñas indicadas como individuos problema en la genealogía,
¿cuántas se espera que manifiesten el fenotipo anormal?
Tal como indicamos en el apartado anterior, lo más probable es que
sean todas heterocigotas, dado que su madre es hija de un hombre sano y
de una mujer que, verosímilmente, debe ser homocigota para el alelo
normal, ya que ha tenido 5 hijos varones y todos ellos son sanos.
La probabilidad de que la abuela fuese heterocigota, a pesar de
5
5 1 
1
p     
32 y, en este caso, la
0 2 
haber tenido 5 hijos sanos es
probabilidad de que la madre fuese heterocigota sería 0,5. Así pues, en
1 1
1
 
este caso, cuya probabilidad es 32 2 64 , se esperaría que las niñas
fueran heterocigotas y la otra mitad de las fueran homocigotas para el
alelo raro.
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
19