Cuidado con los intereses Escuela: _____________________________________________ Fecha: _______________ Plan de clase (1/2)
Anuncio
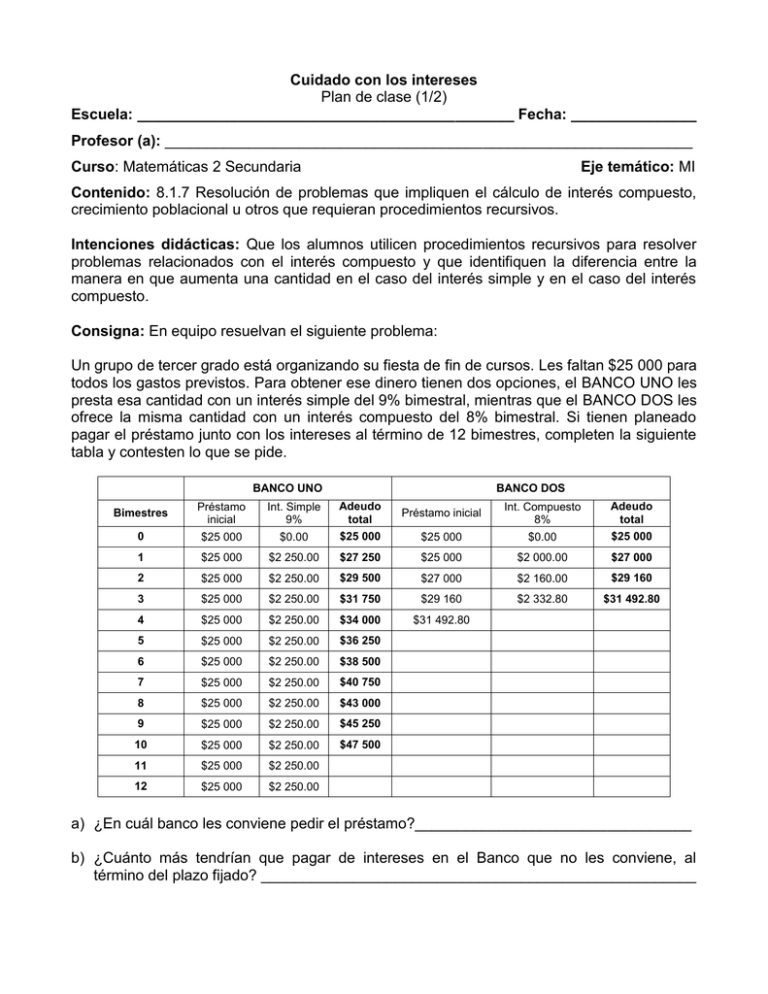
Cuidado con los intereses Plan de clase (1/2) Escuela: _____________________________________________ Fecha: _______________ Profesor (a): _______________________________________________________________ Curso: Matemáticas 2 Secundaria Eje temático: MI Contenido: 8.1.7 Resolución de problemas que impliquen el cálculo de interés compuesto, crecimiento poblacional u otros que requieran procedimientos recursivos. Intenciones didácticas: Que los alumnos utilicen procedimientos recursivos para resolver problemas relacionados con el interés compuesto y que identifiquen la diferencia entre la manera en que aumenta una cantidad en el caso del interés simple y en el caso del interés compuesto. Consigna: En equipo resuelvan el siguiente problema: Un grupo de tercer grado está organizando su fiesta de fin de cursos. Les faltan $25 000 para todos los gastos previstos. Para obtener ese dinero tienen dos opciones, el BANCO UNO les presta esa cantidad con un interés simple del 9% bimestral, mientras que el BANCO DOS les ofrece la misma cantidad con un interés compuesto del 8% bimestral. Si tienen planeado pagar el préstamo junto con los intereses al término de 12 bimestres, completen la siguiente tabla y contesten lo que se pide. BANCO UNO BANCO DOS Bimestres Préstamo inicial Int. Simple 9% Adeudo total Préstamo inicial Int. Compuesto 8% Adeudo total 0 $25 000 $0.00 $25 000 $25 000 $0.00 $25 000 1 $25 000 $2 250.00 $27 250 $25 000 $2 000.00 $27 000 2 $25 000 $2 250.00 $29 500 $27 000 $2 160.00 $29 160 3 $25 000 $2 250.00 $31 750 $29 160 $2 332.80 $31 492.80 4 $25 000 $2 250.00 $34 000 $31 492.80 5 $25 000 $2 250.00 $36 250 6 $25 000 $2 250.00 $38 500 7 $25 000 $2 250.00 $40 750 8 $25 000 $2 250.00 $43 000 9 $25 000 $2 250.00 $45 250 10 $25 000 $2 250.00 $47 500 11 $25 000 $2 250.00 12 $25 000 $2 250.00 a) ¿En cuál banco les conviene pedir el préstamo?_________________________________ b) ¿Cuánto más tendrían que pagar de intereses en el Banco que no les conviene, al término del plazo fijado? ____________________________________________________ Consideraciones previas: Una vez que se discutan las respuestas es importante concluir que en el caso del interés simple, a tiempos iguales corresponden crecimientos iguales ($2 250 cada bimestre) mientras que en el caso del interés compuesto los intereses pasan a formar parte del adeudo total, el cual vuelve a generar nuevos intereses. Cabe señalar que si bien en la tabla se va aumentando el interés simple cada bimestre, también podría calcularse los intereses por los doce bimestres (12 x $2 250), y sumarse esa cantidad al importe del préstamo ($25 000). En cambio, esto no es factible con el interés compuesto pues con éste se necesita conocer, al final de cada bimestre, el adeudo acumulado porque a partir de ese adeudo nuevo se calculan los intereses del siguiente bimestre y así sucesivamente. Una forma de calcular las cantidades que corresponden al BANCO DOS que probablemente los alumnos usarán es la siguiente: se calcula el 8% de $25 000 y suma este resultado ($2 000) a $25 000. Para el siguiente renglón se calcula el 8% de $27 000 y así sucesivamente. Una manera más rápida de calcular el 8% de $25 000 y a la vez sumar ese porcentaje a los $25 000, consiste en efectuar el siguiente producto: $25 000 x 1.08 = $27 000. Esta última cantidad se vuelve a multiplicar por 1.08 para tener el adeudo acumulado del siguiente bimestre y así sucesivamente. La explicación es que 100% de 25 000 + 8% de 25 000 equivale a (1 + 0.08) x 25 000, esto es, a 1.08 x 25 000. Si ningún equipo propone este camino, conviene explicarlo al grupo. Una diferenciación que hay que destacar entre los dos tipos de interés es que en el simple se aprecia que entre cualquier pareja de valores consecutivos se tiene una diferencia constante ($2 250), mientras que en el compuesto la diferencia va aumentando y lo que permanece constante, en cambio, es el cociente entre cualquier pareja de valores consecutivos, por ejemplo: 27000/25000 = 1.08; 29160/27000 = 1.08, etcétera. En otra sesión de trabajo, se puede proponer la siguiente situación problemática: El gobierno del estado ha decidido becar por un año a los alumnos de excelencia. Conocedor de la inteligencia de estos alumnos, sólo becará a aquellos que en menos de 10 minutos elijan la mejor opción de beca. Las opciones son las siguientes: a) Una beca mensual de $500.00 y un bono anual de $1000.00. b) Una beca mensual de $500.00 más un incremento del 10% mensual. Si quisieras ser de los becados, ¿qué opción elegirías y por qué? Observaciones posteriores: 1. ¿Cuáles fueron los aspectos más exitosos de la sesión? ______________________________________________________________________________ ______________________________________________________________________________ ______________________________________________________________________________ 2. ¿Cuáles cambios considera que deben hacerse para mejorar el plan de clase? ______________________________________________________________________________ ______________________________________________________________________________ ______________________________________________________________________________ 3. Por favor, califique el plan de clase con respecto a su claridad y facilidad de uso para usted. Muy útil Útil Uso limitado Pobre Fenómenos poblacionales Plan de clase (2/2) Escuela: ____________________________________________ Fecha: ________________ Profesor (a): _______________________________________________________________ Curso: Matemáticas 2 Secundaria Eje temático: MI Contenido: 8.1.7 Resolución de problemas que impliquen el cálculo de interés compuesto, crecimiento poblacional u otros que requieran procedimientos recursivos. Intenciones didácticas: Que los alumnos utilicen procedimientos recursivos para resolver problemas relacionados con el crecimiento poblacional. Consigna: Organizados en equipos resuelvan el siguiente problema: En el año 2010 la población mundial de la Tierra era de 6 854 millones de habitantes. Suponiendo que la tasa de crecimiento durante una década es de 13% y ésta se mantiene constante, ¿cuál será la población en los años 2020, 2030 y 2040? Consideraciones previas: En el plan anterior se utilizaron procedimientos recursivos para calcular el interés compuesto. Aquí, la clave para resolver el problema y relacionarlo con la recursividad consiste en identificar que para obtener la población en 2040 es necesario conocer la población de la década anterior y que para conocer la población en 2030 es necesario conocer la población en 2020, etcétera. Es importante seguir practicando los cálculos de porcentajes mayores al 100% de una manera directa, en este caso, para calcular el 13% de 6 854 millones, población de 2010, y sumarlo con el 100%, basta con encontrar el resultado de 6 854 x 1.13, expresado en millones. Una vez encontrada la población en 2020 (7 745.02 millones), se repite el proceso para encontrar la población mundial para 2030 y así sucesivamente. Una tabla y una calculadora son dos recursos importantes que permiten ordenar, controlar y calcular los datos del problema. Una tabla como la siguiente puede ser de utilidad: Año 2010 2020 2030 2040 POBLACIÓN MUNDIAL DE LA TIERRA Cálculo para la siguiente década Población 6 854 millones 6 854 x 1.13 7 745.02 millones Con la finalidad de continuar ejercitando procedimientos recursivos, se puede proponer otros problemas como el siguiente: Una cierta cantidad de agua a una temperatura de 80 °C se pone en un congelador que está a 0 °C. En el proceso de enfriamiento se observa que la temperatura se reduce en un 5% por cada minuto que transcurre. a) ¿Cuál es la temperatura del agua después de 4 minutos? b) ¿Después de cuánto tiempo la temperatura del agua desciende a 50 °C? Un problema más complejo es el siguiente: Una población x tiene 52 368 habitantes en la actualidad, si en los últimos 5 años ha crecido a una tasa del 7% anual, ¿cuántos habitantes tenía esa población hace 5 años? Observaciones posteriores: 1. ¿Cuáles fueron los aspectos más exitosos de la sesión? ______________________________________________________________________________ ______________________________________________________________________________ ______________________________________________________________________________ 2. ¿Cuáles cambios considera que deben hacerse para mejorar el plan de clase? ______________________________________________________________________________ ______________________________________________________________________________ ______________________________________________________________________________ 3. Por favor, califique el plan de clase con respecto a su claridad y facilidad de uso para usted. Muy útil Útil Uso limitado Pobre 14/15

