Relatividad de Galileo La primera Teoría de Relatividad fue

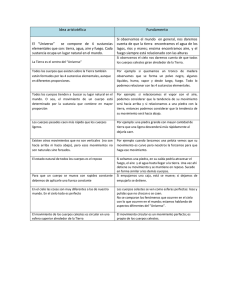
Relatividad de Galileo
La primera Teoría de Relatividad fue desarrollada por Galileo Galilei (1564-1642), creador del método
científico, como resultado de sus estudios sobre movimiento de cuerpos, rozamiento y caída libre.
En sus obras “Diálogo sobre los principales sistemas del mundo" (1632) y “Diálogos acerca de Dos Nuevas
Ciencias” (1636), dio las características de los sistemas de referencia inerciales o “galileanos”, con una
notable descripción de experimentos y su interpretación para dos observadores en movimiento relativo, uno
de ellos sobre un barco que se desplaza suavemente (sin aceleración), y el otro en tierra firme.
Las conclusiones obtenidas permiten postular en sistemas inerciales la equivalencia entre reposo y
movimiento rectilíneo uniforme para dos observadores en movimiento relativo, sentando las bases del
Principio de Inercia.
Asimismo, enunció la relatividad de las trayectorias y de las velocidades de objetos respecto del observador.
Veamos cómo se desarrolla esta Teoría:
Caída de los cuerpos
La primera demostración rigurosa sobre que todos los cuerpos caen con la misma aceleración la dio Galileo
mediante un razonamiento por el absurdo.
Supongamos tener dos cuerpos de distinto peso, material y forma, que los dejamos caer partiendo del reposo
en un sistema inercial. De acuerdo a las ideas aristotélicas el más pesado caería más rápido, como muestra la
figura.
Ahora realicemos la misma experiencia pero agregando un nuevo cuerpo formado por dos objetos idénticos
a los iniciales, ligados entre si (pegados). Para este nuevo objeto durante su caída el de mayor peso está
siendo frenado por el pequeño, que cae más despacio, mientras que el pequeño está siendo acelerado por el
grande, que cae más rápido. En consecuencia el nuevo cuerpo caerá ubicado entre los cuerpos originales,
resultando una contradicción pues es el más pesado. La única solución lógica posible es que todos caigan
igual.
Resuelto el tema anterior, Galileo encaró descubrir la ley de caída, es decir encontrar la función que permita
relacionar la posición con el tiempo durante la caída.
Para ello, siendo Profesor en la Universidad de Pisa (1589), diseñó un modelo experimental que
contemplaba obtener un conjunto de pares de datos correspondientes a posición y tiempo, que obtendría
soltando objetos desde los distintos pisos de la Torre de Pisa. La dificultad principal resultó la medición del
tiempo de caída, que era obtenida con el pulso de un abate. Los resultados no eran precisos ni repetitivos y
no permitieron obtener la ley.
Luego del fracaso inicial decidió determinar los tiempos utilizando una “clepsidra”, que es un recipiente con
agua que tiene una canilla de salida (tapón cónico de madera). El proceso de medición de tiempos consistía
en abrir la canilla cuando soltaba el cuerpo y cerrarla cuando el objeto llegaba al piso. La masa del volumen
de agua recogida lo determinaba con una balanza y era proporcional al tiempo transcurrido.
Lamentablemente, este método tampoco resultó lo suficientemente preciso para asegurar un
comportamiento, por lo cual Galileo concluyó que la dificultad central de este proyecto era la rapidez con
que caían los cuerpos.
Era necesario entonces retrasar la caída de los cuerpos, es decir lograr que caigan más despacio. Luego de
unos importantes estudios sobre fricción, con esferas de madera sobre una tabla lustrada, desarrolló el
“plano inclinado” como dispositivo para retrasar la rapidez de la caída de los cuerpos. No resulta
pretencioso asegurar que el Plano Inclinado de Galileo fue el primer acelerador de partículas en la historia,
y el más importante.
Con este avance experimental obtuvo un conjunto de pares (x,t) que permiten hacer un gráfico de puntos
(x,t) y ajustarle un polinomio, resultando que una parábola es adecuada para dicho ajuste. La ley obtenida
por Galileo fue:
Siendo e el espacio recorrido en un tiempo t, con aceleración constante a.
Nota: Sugiero al lector que analice porqué el polinomio de ajuste no puede ser de grado impar.
Es muy interesante describir, de acuerdo con datos históricos, algunos aspectos sobre cómo Galileo obtuvo
la ley de caída de los cuerpos con el plano inclinado (actividades realizadas en la Universidad de Padua a
partir de 1592).
Si bien este dispositivo permite retardar la caída disminuyendo al ángulo que el plano forma con la
horizontal, dicho ángulo no podía ser muy chico pues, en ese caso, el rozamiento se haría importante y no
podría despreciarse.
Por otro lado, la determinación de los intervalos no era simple, ya que la clepsidra no brindaba la precisión
suficiente y los datos de pruebas repetidas presentaban gran variabilidad, no resultando adecuado para el
objetivo propuesto.
Aunque resulte increíble, Galileo decidió usar un péndulo para medir los tiempos..., y una metodología
genial.
Determinar con precisión lapsos breves con un péndulo suena a disparate, a menos que dichos lapsos se
inicien y terminen exactamente coincidentes con la bolita del péndulo en un extremo de la oscilación, pues
ello es una condición fácilmente distinguible y precisa.
Por ejemplo, si con el péndulo oscilando se suelta la esfera en el plano inclinado (inicio de la caída)
exactamente en el instante en que la oscilación cambia de sentido, y luego se logra que la caída de la
esfera concluya con el péndulo en idéntica posición al cabo de un período completo, el error de medición se
minimiza.
Luego se repite el método para dos períodos, y así sucesivamente.
Obviamente, se deben seleccionar los espacios recorridos en el plano inclinado para que se cumpla la
condición anterior, para 1, 2, 3,..., n oscilaciones. Para ello Galileo usó un tope móvil de madera y ajustó su
posición correcta del final de la caída que corresponda, con el sonido del choque entre la esfera y el tope,
coincidente con la posición del péndulo en un extremo de la oscilación.
Así obtuvo la ley de caída de los cuerpos, que inicialmente se llamó la “Ley de los números impares”,
debido a que los espacios recorridos en cada oscilación del péndulo tenían esa sucesión numérica (ver
figura).
Dado que la suma de los n primeros términos de la sucesión de números impares es n2, se obtiene que el
espacio recorrido es directamente proporcional al cuadrado del tiempo.
Transformaciones de Galileo
Sean dos sistemas de referencia inerciales (O y O’). Llamaremos V (en mayúscula) a la velocidad relativa
entre ellos, v (en minúscula) la velocidad de un objeto respecto de O, y v’ la velocidad respecto de O’. Las
coordenadas espaciales x,y,z se refieren al sistema de O, siendo x’,y’,z’ las correspondientes al sistema del
observador O’.
En general, todas las variables no primadas corresponderán al sistema O y las primadas al O’.
Supongamos que en el instante inicial ambos sistemas coinciden. Para una mejor visualización los esquemas
tendrán al sistema O´debajo del O, y por simplicidad supondremos arbitrariamente que el O está en reposo y
el O´con velocidad constante V en la dirección del eje x.
Supongamos un objeto en reposo en O. Para un observador fijo en O’ este objeto se mueve con
velocidad v'=-V con movimiento rectilíneo uniforme según el eje x’.
La posición del objeto para O’ irá variando según la relación x'=x-V t pues V es constante.
En general, la relación funcional entre las coordenadas de ambos sistemas, conocidas como
Transformaciones de Galileo, serán:
La coordenada temporal es la misma en ambos sistemas.
Estas transformaciones son la base conceptual que fundamentan la “Dinámica del punto material”,
desarrollada por Newton.
Relatividad de las trayectorias
Se deja caer un objeto partiendo del reposo y con coordenadas iniciales (x0 ,y0 ,0), en el sistema O.
Su trayectoria es rectilínea en dicho sistema, como muestra la figura, y se pretende determinar cómo es para
un observador en O’.
En el sistema O el movimiento del cuerpo cumple con
En el sistema O’ la trayectoria estará dada en forma paramétrica, luego de resolver las relaciones
Resolviendo este sistema de dos ecuaciones se obtiene la forma explícita
Esta es la ecuación de una parábola invertida como muestra el gráfico.
La conclusión es que la trayectoria de un objeto es relativa al sistema de referencia. Lo que es una caída
libre rectilínea para un observador será un arco de parábola para otro en movimiento respecto del primero.
Un ejemplo interesante y cotidiano lo ofrece la lluvia. Asumamos que está lloviendo y no hay viento. Para
un observador “en reposo” la lluvia cae verticalmente, mientras que para un observador en movimiento con
velocidad constante las trayectorias de las gotas de agua son rectas inclinadas como muestra la figura.
Se deja planteado demostrar que las trayectorias para O’ no son arcos de parábola debido a que las gotas no
caen en caída libre (MRUV) sino a velocidad constante por la fricción con el aire.
Teorema de adición de velocidades
Este importante Teorema fue demostrado por Galileo en una época en que aún no se conocían las derivadas.
El problema consiste en determinar, para un mismo objeto, como se relacionan las velocidades que le miden
dos observadores inerciales en movimiento relativo. Su demostración es muy simple y sus consecuencias
eran muy conocidas pues se lo aplicaba cotidianamente. Por ejemplo, para subirse a un carro en movimiento
lo mejor es correr hasta ponerse en reposo respecto del carro.
La importancia de este Teorema radica en que Galileo mostró matemáticamente su validez en todos los
sistemas inerciales.
Con las Transformaciones de Galileo podemos relacionar fácilmente las velocidades de un mismo objeto
medidas desde O y O’, resultando:
Teorema de Adición de velocidades
Es decir:
La conclusión es que la velocidad de un móvil es diferente para dos observadores en movimiento relativo.
Las aceleraciones son absolutas
Siendo la aceleración de un punto material la derivada de su velocidad respecto del tiempo, resulta muy
simple encontrar qué valor tendrá en dos sistemas inerciales en movimiento relativo. Derivando la expresión
obtenida en el Teorema de adición de velocidades, obtenemos:
La aceleración de un punto material es absoluta, es decir que su valor es el mismo medido en cualquier
sistema de referencia inercial. Este resultado junto a la invariancia de la masa de un punto material
fundamenta la aseveración de que no hay posibilidad de determinar cual sistema está en reposo y cual en
movimiento mediante experimentos mecánicos, pues las magnitudes Fuerza, Masa y Aceleración son
absolutas.