guiaestudio3 parcial2 diferenciacionparcial optimizacion calculo2 1612 v3f

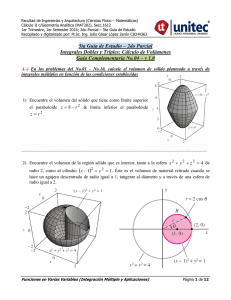
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 2do Parcial – 3era Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
3era Guía de Estudio – 2do Parcial
Derivadas Parciales y Derivación Implícita
Regla de la Cadena en Varias Variables
Optimización en Varias Variables con Derivadas Parciales
Optimización en Varias Variables con Multiplicadores de Lagrange
Guía Complementaria No.03 – v 2.0
Comentarios Generales
Ésta guía cumple única y exclusivamente la función de repaso o complemento de los temas que posiblemente
serán evaluados en el primer examen parcial, además, se establece que en ningún momento ésta guía de estudio
pretende reemplazar el libro de texto y mucho menos, proporcionar un formato de los ejercicios que podrían ser
evaluados en un examen; se hace ésta aclaración para evitar especulaciones y conjeturas erróneas entre los
estudiantes de ésta y las otras secciones de Cálculo II, dado que ésta herramienta ha sido elaborada tomando
como referencia diferentes libros de Cálculo en varias variables y guías de universidades extranjeras, que a
criterio del Catedrático, genera un valor agregado en el conocimiento de los futuros profesionales de la
Ingeniería.
Se le recuerda la importancia de trabajar con disciplina, perseverancia y honestidad cada ejercicio, dado que Ud.
es el único responsable de su éxito o fracaso, el catedrático no es más que un facilitador del conocimiento, por lo
tanto, ante cualquier inquietud no dude en consultarlo.
Instrucciones Específicas de Entrega:
Para que el trabajo grupal sea aceptado y revisado por la totalidad del puntaje, el documento deberá
cumplir las siguientes condiciones:
a) Desarrollo en hojas blancas o rayadas (sin espiral) tamaño carta utilizando ambas caras de la hoja y
como mínimo grapada.
b) Formato de presentación conforme a lo estipulado en el silabo de curso (portada y todos los demás
elementos que apliquen según sea el caso).
c) Los ejercicios deberán estar listados en el orden numérico correlativo de la guía.
d) Todas las páginas que conformen el trabajo (excepto la portada) deberán estar etiquetadas con su
respectivo número de página en la esquina inferior derecha de las mismas y el formato será:
“X de Y”, donde: X = página cualquiera; Y = número total de páginas que forman el trabajo.
e) Ser entregado en la fecha estipulada en el calendario del aula virtual.
A.-) En los problemas del No.01 – No.03, evaluar Fx & Fy en el punto dado
 y

x
1) f  x , y   arctan 
P 2,2 
2) f  x , y   arccos  xy 
P 1,1
3) f  x, y  
2 xy
4x2  5 y 2
P 1,1
Funciones en Varias Variables (Diferenciación Parcial y Aplicaciones)
Página 1 de 15
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 2do Parcial – 3era Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
B.-) En los problemas del No.04 – No.07, para f(x,y), encontrar todos los valores de x & y , tal que
fx(x,y)=0 & fy(x,y)=0 simultáneamente
4) f  x, y   x 2  xy  y 2  2 x  2 y
5) f  x, y   x 2  4 xy  y 2  4 x  16 y  3
2
2
6) f  x, y   e x  xy  y


7) f  x , y   ln x 2  y 2  1
C.-) En los problemas del No.08 – No.11, hallar dy/dx
8) x 2  xy  y 2  x  y  0
9) sec  xy   tan  xy   5  0
10) ln  x 2  y 2   x  y  4


x
11) 2
 y2  6
2
x y
D.-) En los problemas del No.12 – No.14, hallar dw/dt utilizando la regla de la cadena apropiada
12) w  x 2  y 2  z 2 , x  cos t , y  sen t , z  e t
13) w  xy cos  z , x  t , y  t 2 , z  arccos t 
14) w  xy 2  x 2 z  yz 2 , x  t 2 , y  2t , z  2
E.-) En los problemas del No.15 – No.20, hallar w/ r y w/
apropiada
15) w  x 2  xy  y 2 , x  r   ,
utilizando la regla de la cadena
y  r 
Funciones en Varias Variables (Diferenciación Parcial y Aplicaciones)
Página 2 de 15
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 2do Parcial – 3era Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
16) w  arctan  y , x  r cos  , y  rsen  
 x
17) w 
25  5 x 2  5 y 2 , x  r cos  , y  rsen  
y  r   , z  r 2
18) w  xyz , x  r   ,
19) w  x 2  y 2  z 2 , x  rsen  , y  r cos  , z  r 2
20) w  x cos  yz , x  r 2 , y   2 , z  r  2
F.-) En los problemas del No.21 – No.24, demuestre la igualdad planteada utilizando de forma
apropiada los conceptos relacionados con la regla de cadena en una variable y varias variables.
21)
Suponga que w  f  x, y , x  r cos  & y  rsen 
2
2
2
 w 
1
 w 
 w 
  
Demuestre que : 
  2
  
 r 
 x 
r
 y 
 w 


  
2
22)
Suponga que w  f  x, y , x  r cos  & y  rsen 
Demuestre que :
2w
x 2

2w
y 2

2w
1 w 1  2 w




r 2 r r r 2  2
23)
Suponga que w  f r  & r 
Demuestre que :
2w
x
2

2w
y
2

x2  y2  z2
2w
z
2

d 2w
dr
2

2 dw

r dr
24)
Suponga que w  f  x, y  donde x  2u  v & y  u  v
2w
2w
2w 2w 2w
2 2  2  2
Demuestre que : 5 2  2
 x y
x
y
u
v
Funciones en Varias Variables (Diferenciación Parcial y Aplicaciones)
Página 3 de 15
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 2do Parcial – 3era Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
G.-) En los problemas del No.25 – No.28, determine el valor de la incógnita planteada a través de la
optimización de funciones en varias variables.
25) Encuentre el máximo producto posible de tres números positivos cuya suma sea 120.
26) Calcule el volumen máximo posible de una caja rectangular si la suma de las longitudes de sus
12 aristas es igual a 6 metros.
27) Determine las dimensiones de la caja cuyo volumen es 1,000 in3 y que tenga el área superficial
S mínima.
28) Halle las dimensiones de la caja abierta por arriba con volumen de 4,000 cm3 y cuyos cuatro
lados, inferior y laterales, tengan un área total superficial S mínima.
H.-) En los problemas del No.29 – No.32, encuentre las dimensiones que minimicen el costo total del
material necesario para construir la caja rectangular que se describe.
29) La caja ha de estar abierta por arriba, con un volumen de 600.00 in3. El material para su fondo
cuesta 6¢/in2, y para los cuatro lados cuesta 5¢/in2.
30) La caja va a estar cerrada, con un volumen de 48 ft3. El material de la tapa y el fondo cuesta
$3/ft2, y el de sus cuatro lados cuesta $4/ft2.
31) La caja estará cerrada y tendrá un volumen de 750 in3. El material para su tapa y fondo cuesta
3¢/in2, y de su frente y parte posterior 6¢/in2, y el material de sus dos extremos cuesta 9¢/in2.
32) La caja será un cajón cerrado para envíos con un volumen de 12 m3. El material para su fondo
cuesta lo doble (por metro cuadrado) que el de su parte superior y sus cuatro lados.
I.-) En los problemas del No.33 – No.47, determine el valor de la pregunta planteada a través de la
optimización de funciones en varias variables o multiplicadores de Lagrange, esto de acuerdo al
enunciado.
33) Un edificio rectangular va a tener un volumen de 8,000 ft3. Los costos por calefacción y
enfriamiento serán de $2/ft2 para sus paredes superior, del frente y posterior, y de $4/ft2 por las
de los dos extremos. ¿Qué dimensiones del edificio minimizarían dichos costos anuales?
34) Usted desea construir un acuario rectangular con un fondo de pizarra, que cuesta 28¢/in2. Los
lados serán de vidrio, que cuestan 5¢/in2, y la parte superior será de acero inoxidable, que cuesta
2¢/in2. El volumen de este acuario será de 24,000 in3. ¿Cuáles son las dimensiones del que
resulte más barato?
Funciones en Varias Variables (Diferenciación Parcial y Aplicaciones)
Página 4 de 15
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 2do Parcial – 3era Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
35) Una caja rectangular descansa en el plano xy con uno
de sus vértices en el origen. El vértice opuesto está en
el plano como se muestra en la figura. Hallar el
volumen máximo de la caja.
36) Un fabricante de artículos electrónicos determina que la ganancia o beneficio P (en dólares)
obtenido al producir x unidades de un reproductor de DVD & y unidades de un grabador de
DVD se aproxima mediante el modelo


P  x, y   8 x  10 y  0.001 x 2  xy  y 2  10,000
Hallar el nivel de producción que proporciona una ganancia o beneficio máximo. ¿Cuál es la
ganancia máxima?
z
37) Una boya tendrá la forma de cilindro circular recto
cubierto en cada extremo por conos circulares rectos
idénticos con el mismo radio que el cilindro. Encuentre el
área superficial mínima de la boya, dado que tiene un
volumen constante V.
h
z
38) Resuelva el problema No. 37 bajo todas las mismas
condiciones descritas en su enunciado, pero en esta
ocasión se solicita utilizar los multiplicadores de Lagrange
y concluya sobre las respuestas generadas.
Funciones en Varias Variables (Diferenciación Parcial y Aplicaciones)
Página 5 de 15
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 2do Parcial – 3era Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
39) Una ventana pentagonal tendrá la forma de un
rectángulo coronado por un triángulo isósceles (con
base horizontal, de modo que la ventana será simétrica
respecto a su eje vertical), y el perímetro de la ventana
será de 24.00 ft. ¿Cuáles son las dimensiones de una
ventana como esa para la cual entre la mayor cantidad
de luz, gracias a que posea el área máxima?
h
y
x
40) Un rectángulo muy largo de placa metálica tiene un ancho L (línea continua gruesa color negro
en figura de sección transversal) y se va a doblar para formar una canaleta pluvial (ver figura de
isométrico). Calcule las dimensiones de x & θ para maximizar el área de la sección transversal.
Sección Transversal
Isométrico
41) Un contenedor de carga (en forma de un sólido
rectangular) debe tener un volumen de 480.00
pies3. Para su construcción, la parte inferior
costará $5/pie2, los lados y la parte superior
costarán $3/pie2. Usar los multiplicadores de
Lagrange para encontrar las dimensiones del
contenedor de este tamaño que tiene costo
mínimo.
42) Un semicírculo está sobre un rectángulo (ver la figura). Si el área es
fija y el perímetro es un mínimo, o si el perímetro es fijo y el área es
un máximo, utilizar multiplicadores de Lagrange para verificar que
la longitud del rectángulo es el doble de su altura.
Funciones en Varias Variables (Diferenciación Parcial y Aplicaciones)
Página 6 de 15
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 2do Parcial – 3era Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
43) Un tanque industrial tiene forma cilíndrica
con extremos hemisféricos, como se
muestra en la figura. El depósito debe
almacenar 1,000 litros de fluido.
Determinar el radio r y longitud h que
minimizan la cantidad de material utilizado
para la construcción del tanque.
44) Se va a construir un conducto para
agua que va del punto P al punto S
y que debe atravesar por regiones
donde los costos de construcción
difieren (ver la figura). El costo por
kilómetro en dólares es 3k de P a Q,
2k de Q a R & k de R a S. Para
simplificar, sea k = 1. Utilizar
multiplicadores de Lagrange para
localizar x, y & z tales que el costo
total C se minimice.
45) La charola para hielos que se muestra en
la figura va a construirse con un material
que cuesta 3¢/in2. Utilizando
multiplicadores de Lagrange, minimice
una función de costo sujeta a las
restricciones de que cada uno de los 12
compartimientos debe tener sección
transversal cuadrada y de que el volumen
total ha de ser de 12 in3 (ignore el espesor de las separaciones).
46) Un cuarto caliente de almacenamiento tiene la forma de una caja rectangular y un volumen de
1,000 pies3, como se muestra en la figura. Como el aire
caliente sube, la pérdida de calor por unidad de área a
través del techo es cinco veces mayor que la pérdida de
calor a través del suelo. La pérdida de calor a través de
las cuatro paredes es tres veces mayor que la pérdida
de calor a través del suelo. Determinar las dimensiones
del cuarto que minimizan la pérdida de calor y que por
consiguiente minimizan los costos de calefacción.
Funciones en Varias Variables (Diferenciación Parcial y Aplicaciones)
Página 7 de 15
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 2do Parcial – 3era Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
47) La figura muestra un foso de ancho “a”, infestado de cocodrilos, y limitado por cada lado por
una pared de altura “b”. Unos soldados planean cruzar el foso por medio de subir una escalera
colocada entre la pared más cercana según se indica, anclada al terreno por un bloque apropiado
y con el extremo superior directamente por
encima de la pared alejada sobre el lado
opuesto del pantano. Naturalmente, se
preguntan cuál es la longitud mínima L de una
escalera para que sirva para ese propósito. Éste
es un caso particular del problema de minimizar
la longitud de un segmento de recta en el plano
uv que une los puntos P(x,0) y Q(0,y) sobre los
dos ejes coordenados, y que pasa por el punto
dado en el primer cuadrante (a,b).
Demuestre que Lmín = (a2/3 + b2/3)3/2 por medio
de minimizar el cuadrado de la longitud f(x,y) =
x2 + y2 sujeto a la restricción de que satisfaga la
ecuación (a/x)+(b/y)=1 de la recta que pasa por
P y Q.
PROBLEMAS ADICIONALES DE REPASO Y/O CONSOLIDACIÓN DE CONCEPTOS
(No forman parte de la entrega de ejercicios para fines acumulativos de guías de estudio)
48) Determine las dimensiones de la caja rectangular con el mayor volumen si el área superficial
total es de 64.00 cm2.
49) Determine las dimensiones de una caja rectangular de volumen máximo tal que la suma del
largo de sus 12 aristas es una constante c.
50) La base de un acuario de volumen constante V está hecho de pizarra y los lados son de vidrio.
Si la pizarra cuesta cinco veces más por unidad de área que el vidrio, determine las dimensiones
del acuario que minimizan el costo de los materiales.
51) Una caja de cartón sin tapa debe tener 32,000 cm3. Calcule las dimensiones que minimicen la
cantidad de cartón utilizado.
52) Está en proceso de diseño un edificio rectangular para que minimice las pérdidas de calor. Los
muros oriente y poniente pierden calor a razón de 10 unidades/m2 por día, los muros del norte y
del sur pierden 8 unidades/m2 por día, el piso pierde 1 unidad/m2 por día, y el techo pierde 5
unidades/m2 por día. Cada muro debe medir por lo menos 30 m de largo, la altura debe ser por
lo menos de 4 m y el volumen debe ser exactamente 4,000 m3.
a) Encuentre las dimensiones que minimizan la pérdida de calor.
b) ¿Podría diseñar un edificio con menos pérdida de calor si las restricciones de las longitudes
de los muros se eliminaran?
Funciones en Varias Variables (Diferenciación Parcial y Aplicaciones)
Página 8 de 15
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 2do Parcial – 3era Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
53) La temperatura en un punto (x, y) de una placa de metal es T  x, y   4 x 2  4 xy  y 2 . Una
hormiga camina sobre la placa alrededor de una circunferencia de radio 5 con centro en el
origen. ¿Cuáles son las temperaturas máxima y mínima encontradas por la hormiga?
54) Se ha pedido a su empresa diseñar un tanque de almacenamiento para concentrado de jugo de
naranja. Las especificaciones del cliente demandan un tanque cilíndrico con extremos
semiesféricos, y el tanque debe alojar 8,000 m3 de jugo de naranja. El cliente también quiere
usar la menor cantidad posible de material en la construcción del tanque. ¿Qué radio y altura
recomendaría para la porción cilíndrica del tanque?
55) Usted es el encargado de instalar un radiotelescopio en un planeta recién descubierto. Para
minimizar la interferencia, quiere colocar el radiotelescopio donde el campo magnético del
planeta sea más débil. El planeta es esférico, con un radio de 6 unidades. Con base en un
sistema de coordenadas cuyo origen es el centro del planeta, la fuerza del campo magnético está
dada por M  x, y , z   6 x  y 2  xz  60 . ¿Dónde debe ubicar el radiotelescopio?
56) Calcule las dimensiones de la lata cilíndrica circular recta y cerrada con menor área superficial
cuyo volumen sea de 16π cm3.
57) Determine el radio y la altura del cilindro circular recto y abierto de mayor área superficial que
puede inscribirse en una esfera de radio “a”. ¿Cuál es la mayor área superficial?
58) Use el método de multiplicadores de Lagrange para encontrar las dimensiones del rectángulo de
mayor área que se puede inscribir en la elipse
x2 y2

 1 , con lados paralelos a los ejes
16
9
coordenados.
59) En una fábrica, los trabajadores se han clasificado en dos maneras: A y B. Los trabajadores tipo
A ganan $14 por jornada, mientras que los del tipo B ganan $13. Para alcanzar cierta
producción en una jornada, se ha determinado aumentar los salarios de los trabajadores, si se
emplean x trabajadores del tipo A & y trabajadores del tipo B, entonces el número de dólares
del costo de la jornada es y 3  x 2  8 xy  600 . ¿Cuántos trabajadores de cada tipo deben
emplearse a fin de que el costo de la jornada sea un mínimo si se requieren por lo menos tres
trabajadores de cada tipo para una jornada?
60) Una compañía tiene tres fábricas y todas elaboran el mismo producto. Si la fábrica A produce x
unidades, la fábrica B produce y unidades y la fábrica C produce z unidades, entonces sus
respectivos costos de producción son:
2 z
2

3x 2  200 
dólares,
y 2  400 
dólares &
 300 dólares. Si se va a surtir un pedido de 1100 unidades, emplee los multiplicadores
de Lagrange para determinar cómo debe distribuirse la producción entre las tres fábricas a fin
de minimizar el costo total de producción.
Funciones en Varias Variables (Diferenciación Parcial y Aplicaciones)
Página 9 de 15
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 2do Parcial – 3era Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
61) La figura muestra un hexágono con vértices (0, ±1) &
(±x, ±y) inscrito en la circunferencia unitaria x2 + y2 = 1.
Demuestre que su área es máxima cuando la figura
pintada representa un hexágono regular con lados iguales.
62) Cuando el hexágono del ejercicio No.61 se gira alrededor del eje
“y”, genera un sólido de revolución que consiste en un cilindro y
dos conos (tal como se puede apreciar en la figura mostrada). ¿Cuál
es el radio y altura del cilindro que maximizan el volumen de este
sólido geométrico regular?
63) Una inyección de x miligramos de cierto medicamento A & y miligramos del medicamente B,
produce una respuesta de R unidades, misma que se describe a través de R  x 2 y 3 c  x  y  ,
donde c es una constante positiva. ¿Qué dosis de cada medicamente ocasionarán la máxima
respuesta?
64) Calcule el volumen del mayor paralelepípedo rectangular que pueda inscribirse en el elipsoide
36 x 2  9 y 2  4 z 2  36 , si las aristas deben ser paralelas a los ejes coordenados.
65) Se elabora una caja rectangular sin tapadera con un costo total por material de $10. Si el
material para el fondo de la caja cuesta $0.15/pie2 y el material para los lados cuesta $0.30/pie2;
determine las dimensiones de la caja de mayor volumen que pueda elaborarse.
66) Se construye una caja rectangular cerrada con un volumen de 16 pie3 empleando tres tipos de
materiales. El costo del material para el fondo y la tapadera es de $0.18/pie2, el costo del
material para el frente y parte posterior es de $0.16/pie2, y el costo del material para los otros
dos lados es de $0.12/pie2. Calcule las dimensiones de la caja de modo que el costo de los
materiales sea mínimo.
Funciones en Varias Variables (Diferenciación Parcial y Aplicaciones)
Página 10 de 15
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 2do Parcial – 3era Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
67) Determine las dimensiones de una caja rectangular con un volumen de 1 pie3 que tiene un área
superficial mínima S.
68) Encuentre el punto sobre el plano x  2 y  z  1 más cercano al origen. (sugerencia: considere
el cuadrado de la distancia.)
69) El pentágono que se muestra en la figura, formado por un
triángulo isósceles sobrepuesto sobre un rectángulo, tiene
perímetro fijo P. Calcule x, y & θ de manera que el área del
pentágono sea un máxima.
70) Un pedazo de latón de 24 pulg de ancho se dobla de
manera tal que su sección transversal es un
trapezoide isósceles. Calcule x & θ de manera que
el área de la sección transversal sea un máximo.
¿cuál es el área máxima?
71) Un tanque cilíndrico recto se le superpone una tapadera cónica en la
forma que se ilustra en la figura. El radio del tanque es de 3m, y su
área superficial total corresponde a 81π cm2. Calcule las alturas x &
y de manera que el volumen del tanque sea máximo.
72) Encuentre el área máxima de un triángulo rectángulo cuyo perímetro es de 4 pies.
Funciones en Varias Variables (Diferenciación Parcial y Aplicaciones)
Página 11 de 15
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 2do Parcial – 3era Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
Referencias Bibliográficas Utilizadas en la Elaboración de ésta Guía de Estudio
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
Purcell, E. (2009). Cálculo 1, 1ª ed. México D.F, México. Pearson Educación.
Leithold, L. (1998). El Cálculo. 7ª ed. México D.F, México. Oxford University Press – Harla México, S.A.
Stewart, J. (2002). Cálculo, Trascendentes Tempranas, 4ª ed. México D.F, México. Thomson Editores.
Zill, D. (1994). Cálculo con Geometría Analítica, 1ª ed. México D.F, México. Grupo Editorial
Iberoamericana.
Stewart, J. (2008). Cálculo Varias Variables, Trascendentes Tempranas, 6ª ed. México D.F, México.
Cengage Learning Editores.
Stewart, J. (2012). Cálculo Varias Variables, Trascendentes Tempranas, 7ª ed. México D.F, México.
Cengage Learning Editores.
Edwards, H.; Penney, D. (2008). Cálculo con Trascendentes Tempranas, 7ª ed. México D.F, México.
Pearson Educación.
Thomas, G. (2010). Cálculo Varias Variables, 12ª ed. México D.F, México. Pearson Educación.
Zill, D. (2011). Cálculo Varias Variables. Trascendentes Tempranas, 4ª ed. México D.F, México. McGrawHill Educación.
Larson, R.; Edwards, B. (2010). Cálculo 2 de Varias Variables, 9ª ed. México D.F, México. McGraw-Hill
Educación.
Zill, D.; Wright, W. (2011). Matemáticas 3. Cálculo de Varias Variables. 1ª ed. México D.F, México.
McGraw-Hill Educación.
Juárez, I.; Moreno, J.; Tomeo, V. (2007). Cálculo en Varias Variables Paso a Paso. 1ª ed. Madrid, España.
Thomson Editores.
Cálculo Diferencial e Integral. Ingeniería Matemática; Facultad de Ciencias Físicas y Matemáticas.
Universidad de Chile. Santiago de Chile.
Carrasco, P.; Torres, G. (2008). Matemáticas IV – Cálculo Integral, 1ª ed. México. Cengage Learning
Editores.
Cortes, I. (1978). Cálculo Elemental. Universidad Nacional Experimental de Táchira. Táchira, República
Bolivariana de Venezuela.
Rojas, D. Matemáticas II: Ingeniería Mecánica y Química. Instituto Universitario de Tecnología “José
Antonio Anzoátegui”. República Bolivariana de Venezuela.
Universidad de Santiago de Chile, (2001-2010). Pruebas acumulativas y exámenes parciales Cálculo 10001.
Santiago de Chile, Chile.
Jiménez, B. Cruz, L. Meza, M. (2009). Elementos de Cálculo Integral. 1ª ed. Instituto Tecnológico y de
Estudios Superiores de Monterrey (ITESM). México. Limusa, Grupo Noriega Editores.
JUCELO1209® D.R.2016
--------------------------------------------------------------------------------------------------------------------------
Listado De Soluciones Aproximadas Para Los Ejercicios Propuestos
A.-) En los problemas del No.01 – No.03, evaluar Fx & Fy en el punto dado
1) R/= f x 2,2   f y 2,2   1
4
2) R/= f x 1,1 no definido f y 1,1 no definido
3) R/= f x 1,1  10
27
; f y 1,1  8
27
Funciones en Varias Variables (Diferenciación Parcial y Aplicaciones)
Página 12 de 15
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 2do Parcial – 3era Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
B.-) En los problemas del No.04 – No.07, para f(x,y), encontrar todos los valores de x & y , tal que
fx(x,y)=0 & fy(x,y)=0 simultáneamente
4) R/=> x  2; y  2
5) R/=> x  6; y  4
6) R/=> x  y  0
7) R/=> x  y  0
C.-) En los problemas del No.08 – No.11, hallar dy/dx
8) R/=> dy
9) R/=> dy
10) R/=> dy
11) R/=> dy
dx
dx
dx
dx
  y  2 x  1
y
2 y  x  1
x

2
2
 xx  y

2
2
 y x
 2 2
y  x  y 

2 xy  2 yx 4  4 x 2 y 3  2 y 5 
D.-) En los problemas del No.12 – No.14, hallar dw/dt utilizando la regla de la cadena apropiada
12) R/=> dw
13) R/=> dw
14) R/=> dw
dt
dt
dt
 2e 2t
 4t 3
 24t 3  8
Funciones en Varias Variables (Diferenciación Parcial y Aplicaciones)
Página 13 de 15
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 2do Parcial – 3era Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
E.-) En los problemas del No.15 – No.20, hallar w/ r y w/
apropiada
15) R/=> w
16) R/=> w
17) R/=> w
18) R/=> w
19) R/=> w
r
r
r
r
 2 r ; w
 0; w
  5r


 6
1
25  5r

2
; w

  2 3 r 2   2 ; w


 2 r 1   4 ; w



0

 2 r r 2  2 2
r

 r 2 4 3


w
 6 r 2 2  2 r 3 sen r   2  2 3 

w
20) R/=>
r
utilizando la regla de la cadena

 cos r   2  2 3  2 r  r 2 2 sen r   2  2 3

G.-) En los problemas del No.25 – No.28, determine el valor de la incógnita planteada a través de la
optimización de funciones en varias variables.
25) R/→ x=y=z=40; P=64,000
26) R/→ x=y=z=1/2m; V=1/8m3
27) R/→ x=y=z=10in; A=600in2
28) R/→ x=y=20cm; z=10cm
H.-) En los problemas del No.29 – No.32, encuentre las dimensiones que minimicen el costo total del
material necesario para construir la caja rectangular que se describe.
29) R/→ x=y=10in; z=6in; C=$18
30) R/→ x=y=4ft; z=3ft; C=$288.00
31) R/→ x=10in; y=15in; z=5ft; C=$27.00
32) R/→ x=y=2m; z=3m; C=36.00
Funciones en Varias Variables (Diferenciación Parcial y Aplicaciones)
Página 14 de 15
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 2do Parcial – 3era Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
I.-) En los problemas del No.33 – No.47, determine el valor de la pregunta planteada a través de la
optimización de funciones en varias variables o multiplicadores de Lagrange, esto de acuerdo al
enunciado.
33) R/→ x=20ft; y=40ft; z=10ft; C=$4,800.00
34) R/→ x=y=20in; z=60in; C=$360.00
35) R/→ x=4/3; y=2in; V=64/9 und3
36) R/→ x=2000 unds; y=4000unds; P=$18,000
2
37) R/→ r  6 9V
20
2
unds , z  h  3 12V
25
unds
38) R/→ igual que el ejercicio No.50
39) R/→ x=6.43ft; h=1.86ft; y=5.071ft; A=38.58ft2
2
40) R/→ x=L/3; A= L
3
12
unds 2 .
41) R/→ x=y=7.11pies; z=9.49pies; C=
42) R/→
43) R/→ r=6.20unds; h=0.014unds
44) R/→ x=0.707Km; y=0.577Km; z=8.716Km
45) R/→ x=6.6in; y=2.2in; z=0.82in; C= (respuestas con un costo unitario de 1c/in2)
46) R/→ x=y=z=10pies; C=
Funciones en Varias Variables (Diferenciación Parcial y Aplicaciones)
Página 15 de 15