7.1 planteamiento de la ecuación del transporte radiativo

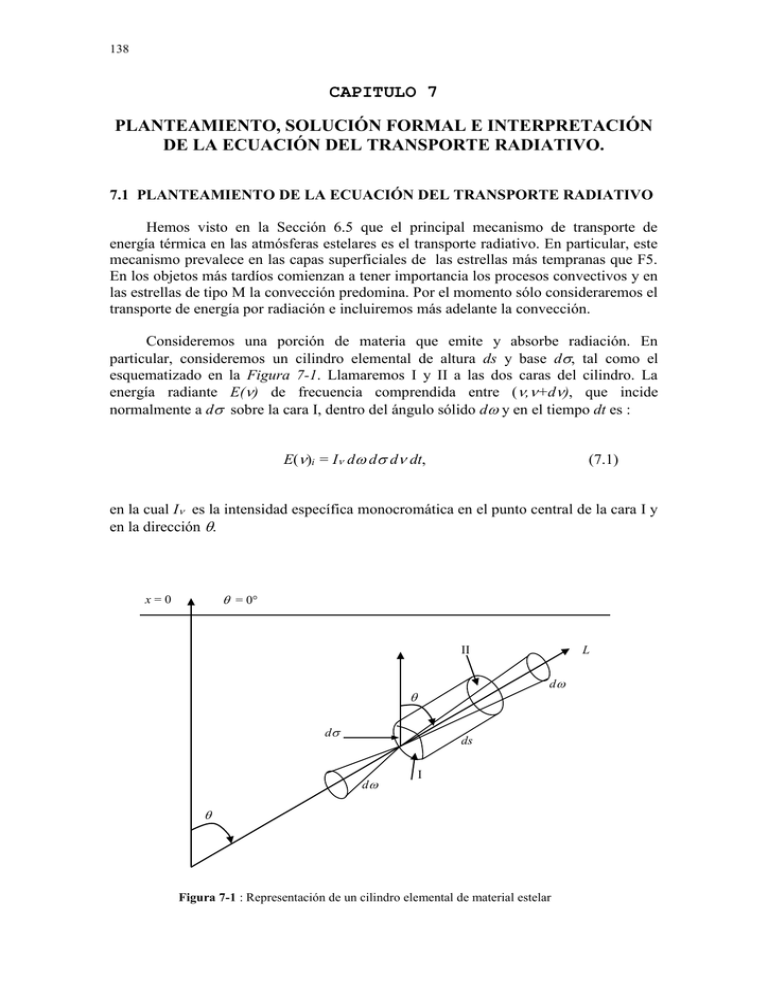
138
CAPITULO 7
PLANTEAMIENTO, SOLUCIÓN FORMAL E INTERPRETACIÓN
DE LA ECUACIÓN DEL TRANSPORTE RADIATIVO.
7.1 PLANTEAMIENTO DE LA ECUACIÓN DEL TRANSPORTE RADIATIVO
Hemos visto en la Sección 6.5 que el principal mecanismo de transporte de
energía térmica en las atmósferas estelares es el transporte radiativo. En particular, este
mecanismo prevalece en las capas superficiales de las estrellas más tempranas que F5.
En los objetos más tardíos comienzan a tener importancia los procesos convectivos y en
las estrellas de tipo M la convección predomina. Por el momento sólo consideraremos el
transporte de energía por radiación e incluiremos más adelante la convección.
Consideremos una porción de materia que emite y absorbe radiación. En
particular, consideremos un cilindro elemental de altura ds y base d, tal como el
esquematizado en la Figura 7-1. Llamaremos I y II a las dos caras del cilindro. La
energía radiante E() de frecuencia comprendida entre (,+d), que incide
normalmente a d sobre la cara I, dentro del ángulo sólido d y en el tiempo dt es :
E()i = I d d d dt,
(7.1)
en la cual I es la intensidad específica monocromática en el punto central de la cara I y
en la dirección .
 = 0°
x=0
II
L
d

d
ds
d
I

Figura 7-1 : Representación de un cilindro elemental de material estelar
139
La intensidad que emerge normalmente de la cara II será I + dI, en la cual dI
representa el incremento de la intensidad específica monocromática debido a los
procesos de absorción y emisión que ocurrieron dentro del cilindro. Este incremento
puede en principio ser positivo, negativo o nulo. En consecuencia, la energía radiante
E()e de frecuencia comprendida entre  y ( + d) que emerge normalmente de la cara
II del cilindro elemental, dentro del ángulo sólido d y en el tiempo dt será :
E()e = (I + dI) d d d dt
(7.2)
Teniendo en cuenta la expresión (6.51), la cantidad de energía con frecuencias
comprendidas entre  y ( + d), emitida dentro del cilindro en la dirección d y en el
tiempo dt es :
E()em =  dV d d dt
Puesto que  = j y dV = d ds , se tiene :
E()em = j ds d d d dt
(7.3)
Por otra parte, la cantidad de energía absorbida dentro del cilindro elemental
puede expresarse de la siguiente manera :
E()abs = -  E()i ds,
la cual es formalmente idéntica a la expresión (6.45). Reemplazando en la expresión
anterior el valor de E()i de (7.1), se obtiene :
E()abs = - I ds d d d dt
(7.4)
Si se admite que la energía que emerge de la cara II del cilindro elemental debe
ser igual a la que penetró por la cara I, más la que se creó dentro del cilindro,
disminuida por la cantidad que éste absorbió, se tiene :
E()e = E()i + E()em + E()abs
(7.5)
140
En virtud de las expresiones (7.1), (7.2), (7.3) y (7.4), la igualdad anterior se
transforma en la siguiente ecuación diferencial :
dI
 j    I ,
ds
(7.6)
conocida como ecuación general del transporte radiativo. Esta ecuación describe los
cambios que sufre la intensidad específica monocromática a medida que un rayo de
intensidad I atraviesa un medio que absorbe y emite con coeficientes  y j,
respectivamente, siendo  la densidad del medio y ds la trayectoria elemental seguida
por el rayo.
7.2 ECUACIÓN DEL TRANSPORTE RADIATIVO EN COORDENADAS
ESFÉRICAS
Sea una estrella esférica cuyo centro está en C (Figura 7-2). Supongamos además
que L1 y L2 representan dos direcciones coincidentes con sendos radios estelares,
separadas por el ángulo elemental d. Consideremos dos puntos A y B en la fotósfera de
la estrella, ubicados a distancias r y r’ del centro de la misma, respectivamente. Tal
como se aprecia en la Figura 7-2, al pasar desde A hacia B siguiendo la trayectoria
elemental ds, el cambio dr en la coordenada radial puede escribirse de la siguiente
manera :
dr = ds cos 
(7.7)
Además puesto que rd = - ds cos(90° - ), resulta :
d
sen 

,
ds
r
(7.8)
en la cual el signo menos se debe a que el ángulo  disminuye a medida que ds
aumenta.
Si aceptamos que I no depende del ángulo  (simetría esférica), entonces I sólo
dependerá de las otras dos coordenadas esféricas: r y . Por lo tanto, el cambio que
experimentará la intensidad específica monocromática I al pasar del punto A hacia el B
siguiendo la trayectoria infinitesimal ds, será :
dI I dr I d
I
sen  I

. 
.
 cos  .  
.
ds
r ds  ds
r
r 
141
d
L1


L2
’
ds
r
r + dr = r’
d
C
Figura 7-2: Modelo geométrico de una atmósfera estelar. Relación
entre las coordenadas esféricas y lineales.
La ecuación del transporte radiativo (7.6) puede ahora escribirse en coordenadas
esféricas de la siguiente manera :
cos 
I sen  I

 j  -  I
r
r 
(7.9)
A medida que nos desplazamos según la trayectoria elemental ds, van variando las
coordenadas r y  y en consecuencia va cambiando I. Es importante destacar que no
obstante estar considerando una dirección fija, el ángulo  cambia al pasar desde el
punto A al punto B (ver Figura 7-2).
Si el radio de la estrella es mucho mayor que el espesor h de la atmósfera, la
expresión (7.8) se hace despreciable frente a la (7-7). En efecto, dado que la coordenada
radial r y la profundidad geométrica x de un punto de la atmósfera se miden según la
misma dirección, pero x aumenta por valores negativos, podemos escribir :
r = R + x = R(1 + x/R),
en la cual R es el radio de la estrella.
142
Escribiremos ahora la derivada d/ds de la siguiente manera :
d
sen
sen
h


.
x
x R
ds


R 1  
h1  
 R
 R
Puesto que el sen no puede exceder la unidad, tenemos :
d
1
h

.
x R
ds

h1  
R

(7.10)
Si h  R, d/ds tiende a cero. Es decir, si el espesor atmosférico es
despreciable frente al radio estelar, el ángulo  se mantiene constante a medida que nos
desplazamos según la trayectoria elemental ds y por consiguiente la derivada d /ds
tiende a cero. La ecuación del transporte radiativo se reduce ahora a la siguiente
expresión :
cos 
dI
 j     I
dr
(7.11)
El caso considerado en que h  R permite transformar el problema esférico en
plano. En otras palabras, si h  R puede concebirse a la fotosfera como constituida por
capas plano-paralelas. Si esta aproximación no es válida, debe considerarse el caso
esférico.
Utilizando como antes la variable x (profundidad geométrica) en lugar de la
coordenada radial, la ecuación (7.11) resulta :
cos 
dI
 j    I
dx
(7.12)
Dividiendo ambos miembros de (7.12) por - obtenemos finalmente :
cos
dI
 I  S
d
(7.13)
143
Esta ecuación es válida para una atmósfera plano-paralela. Si las capas son
esféricas, un rayo cualquiera que parta de algún punto de la atmósfera seguirá una
trayectoria tal que no formará el mismo ángulo  con respecto a las normales a las
diferentes capas. En este caso, el ángulo  varía a medida que el rayo de intensidad I
sigue su trayectoria. Tal como ilustra la Figura 7-3, en este caso los ángulos 1, 2, 3,
... son todos diferentes, lo que implica d / ds  0.
3
rayo
2
1
centro
Figura 7-3: Variación del ángulo  en una atmósfera con capas esféricas
Por el contrario, en una atmósfera de capas plano-paralelas, el ángulo  no varía a
medida que el rayo de intensidad I sigue su trayectoria (Figura 7-4). En este caso, 1 =
2 = 3 = ... y por ende d /ds = 0.
rayo
3
2
1
centro
Figura 7-4: Variación del ángulo  en una atmósfera de capas planas y
paralelas.
144
La suposición de que las capas son plano-paralelas puede hacerse en virtud de la
pequeña curvatura real de las atmósferas estelares. No es necesario que toda la estrella
sea absolutamente plana; es suficiente aceptar que las capas atmosféricas puedan
considerarse plano-paralelas en cada radio individual (Figura 7-5).
superficie estelar
 = 0°
 = 0°
Figura 7-5: Esquema ilustrativo del significado real de
la suposición de capas planas y paralelas.
7.3 CONDICIONES DE CONTORNO
Hemos ya planteado la ecuación general del transporte radiativo. Nuestro
problema inmediato será resolver esta ecuación. Puesto que se trata de una ecuación
diferencial, tendremos que fijar algunas condiciones de contorno acordes con la
geometría del problema. Consideraremos a continuación dos casos de interés astrofísico,
a saber : una capa de espesor finito y una atmósfera semi-infinita.
7.3.1 Capa de espesor finito
Sea una capa tal como la esquematizada en la Figura 7-6. Dicha capa puede
incluir cualquier tipo de material y supondremos que fuera de ella sólo existe el vacío.
En la figura hemos indicado la dirección hacia el observador y hemos denominado
frontera inferior y superior a las superficies que limitan la capa. Por convención,
supondremos que la frontera superior se enfrenta con un hipotético observador.
Denotaremos X a la profundidad geométrica total de la capa y T a la correspondiente
profundidad óptica total. Dichas profundidades crecen en sentido contrario y
supondremos x = 0 y  = 0 en la frontera superior. Mediremos el ángulo  en el
sentido indicado en la figura, de manera que  = cos  tendrá valores negativos para los
rayos que inciden sobre la frontera superior y valores positivos para aquéllos que
inciden sobre la frontera inferior.
145
En general, denotaremos con I (,) a la intensidad específica monocromática de
un rayo en un punto a profundidad óptica  que forme un ángulo  ( = cos ) con la
dirección hacia el observador. Imponer condiciones de contorno en este caso particular
significa especificar los valores de la función I en las dos fronteras. Es decir, debemos
indicar el valor de la función I(0,) = f() para –1   < 0 (frontera superior) y de la
función I(T,) = g () para 0 <   1 (frontera inferior).
profundidad
geométrica
X
x=0

observador
 = 0
frontera
superior
radiación
 = T
frontera
inferior
Figura 7-6: Capa de espesor finito.
7.3.2 Atmósfera semi-infinita
Este caso, esquematizado en la Figura 7-7, constituye la aproximación que
usualmente se hace de una atmósfera estelar. Establecer condiciones de contorno en esta
geometría significa especificar la radiación incidente en la frontera superior o superficie
de la fotosfera. Usualmente se acepta que no incide radiación sobre la superficie estelar
y, en consecuencia, I(0,) = f() = 0 para –1   < 0. En la frontera inferior la
condición de contorno se expresa de la siguiente manera :
lím I (  ,  )e  /   0 ,
  
para todos los rayos con 0 <   1.
(7.14)
146
En este caso no existe frontera inferior porque admitimos que la fotosfera es
semi-infinita. La condición de contorno (7.14) significa simplemente que la radiación
proveniente de capas muy profundas no llega a la superficie.
frontera
superior
fotosfera
 = 0
superficie
Figura 7-7: Atmósfera semi-infinita, aproximación que
usualmente se hace de una atmósfera estelar
7.4 SOLUCIÓN DE LA ECUACIÓN DEL TRANSPORTE RADIATIVO EN
CASOS PARTICULARES
Supongamos un campo radiante en el que no existe ningún tipo de materia,
solamente radiación. Dado que en este caso  = 0, la solución de la ecuación del
transporte radiativo (7-12) es simplemente : I(x) = constante. Este resultado ya nos es
conocido puesto que hemos mostrado en la Sección 6.6.1 que en ausencia de fuentes y
sumideros, la intensidad específica monocromática de un rayo luminoso se mantiene
invariable en toda su trayectoria.
Supongamos ahora que en el campo radiante existe material que sólo puede
emitir radiación, siendo incapaz de absorberla ( = 0). La ecuación (7-12) se
transforma entonces en :
dI =
1

j dx
147
Si se trata de una capa de espesor finito, integrando la ecuación anterior entre  =
T y  = 0, obtenemos :
I (0,) = I (T, ) +
1
0
 x
j ( x)  ( x)dx ,
(7.15)
válida para 0 <   1.
Puesto que ds= dx/cos, al comparar la expresión (6.55) con el segundo término
de (7.15) se advierte claramente que dicho término representa la intensidad específica
monocromática creada en la capa durante la trayectoria del rayo en la dirección . Por
lo tanto, la expresión (7.15) expresa que cuando un rayo incide sobre la frontera inferior
de una capa finita, en la frontera superior de la misma se recibe la intensidad específica
monocromática I(T,) que incidió sobre la frontera inferior, más la cantidad creada en
la capa que llega en esa misma dirección.
Si en lugar de una capa finita hubiéramos considerado una atmósfera semi-infinita
en la cual la materia sólo puede emitir radiación, el primer término del segundo
miembro de (7-15) sería nulo en virtud de la condición de contorno (7-14), en tanto que
la integral resultante carecería de sentido físico.
Otra posibilidad consiste en suponer material que sólo puede absorber radiación
(j = 0). En este caso, la ecuación del transporte radiativo (7-12) resulta :
dI
1
    dx
I

Para el caso de una capa de espesor finito, integrando la ecuación anterior entre 
= T y  = 0, obtenemos :
I (0,  )
1
    dx
I (T ,  )
x
0
ln
(7.16)
Si ahora integramos la (6.48) entre  = T y  = 0, veremos que la integral del
segundo miembro de (7.16) equivale a la profundidad óptica total T de la capa. En
consecuencia, la solución de la ecuación del transporte radiativo para una capa de
espesor finito con material que sólo puede absorber radiación, es la siguiente :
I(0, ) = I(T, ) eT / 
válida para 0 <   1.
(7.17)
148
En este caso particular que estamos considerando, cuando un rayo luminoso
incide sobre la frontera inferior de una capa finita que sólo puede absorber radiación, la
intensidad específica monocromática que emerge por la frontera superior de la capa en
una determinada dirección , es igual a la intensidad que incide sobre la frontera
inferior en la dirección considerada atenuada por el factor e T /  , el cual tiene en cuenta
la absorción del rayo luminoso dentro de la capa.
7.5 SOLUCIÓN FORMAL DE LA ECUACIÓN DEL TRANSPORTE
RADIATIVO
Vamos ahora a considerar el caso general de una fotosfera en la cual existe
material en condiciones de absorber y emitir radiación. Nuestro propósito es encontrar
una solución general de la ecuación del transporte radiativo (7.13), obtenida para una
atmósfera plano-paralela. Haciendo nuevamente la sustitución  = cos , la ecuación a
resolver es la siguiente :

dI
 I  S
d 
(7.18)
Se trata pues de una ecuación diferencial lineal, de primer orden y con
coeficientes constantes. Para encontrar la solución general multiplicamos ambos
miembros de (7.18) por el factor de extinción e /  y dividimos luego por la variable
. Así obtenemos :

dI  /  I e / 
Se 
e

 
d


/
Luego :
S e  / 
d
 / 
I e

d 



Integrando la ecuación anterior entre dos profundidades ópticas  1 y   2 se tiene:
I (  2 ,  )e
 2 / 
 I (  1 ,  )e
 1 / 
-
 2
 S (t )e

1
 t / 
dt

,
149
en la cual t es la profundidad óptica  tomada como variable de integración.
 / 
Multiplicando ambos miembros de la expresión anterior por e  1
y despejando
I (1 ,  ) resulta :
I (  1 ,  )  I (  2 ,  )e
 ( 2  1 ) / 

 2
 S (t )e

t / 
1
dt
(7.19)

Para comprender el significado físico de la solución general (7.19) regresaremos
por un momento a los dos casos particulares antes considerados: la capa de espesor
finito y la atmósfera semi-infinita.
En el primer caso (capa finita), consideraremos  1  0 (frontera superior) y  2
= T (frontera inferior). La (7.19) se escribirá ahora de la siguiente manera :
I(0,) = I (T,) e
T / 
T
+
 S (t )e
0
 t / 
dt

,
(7.20)
válida para 0 <   1.
El primer término del segundo miembro de (7.20) representa claramente la
intensidad específica que alcanza la frontera superior de la capa según la dirección ,
proveniente de la frontera inferior cuya profundidad óptica es T. La exponencial eT / 
es el factor de extinción en la dirección considerada. Por su parte, el segundo término
del segundo miembro de (7.20) representa la intensidad específica monocromática
emitida en cada punto de la capa en la dirección considerada, correspondientemente
atenuada por el factor de extinción e integrada sobre todo el espesor óptico de la capa.
Esta última aseveración se constata fácilmente si se tiene en cuenta la expresión (6.55).
En efecto, de acuerdo a esa expresión, el incremento de la intensidad específica dI
producido por una masa de densidad  que emite en la dirección de propagación ds es
j ds, o bien, j dx/cos. Si expresamos dx en función de d, el incremento anterior
dI debería ser: -S d/cos. La fracción de intensidad creada en cada punto que
alcanza la frontera superior de la capa será pues: - S e /  (1/cos). Integrando esta
última expresión sobre todo el espesor óptico de la capa finita (entre T y 0) y
cambiando los límites de integración, se obtiene el segundo término del segundo
miembro de la expresión (7.20). Si se considera el caso en que  1 = T ,  2 = 0 y
valores de  negativos, se obtiene entonces la expresión de la radiación emergente por
la frontera inferior.
En el caso particular de que la función fuente S sea constante dentro de la capa y
que no haya intensidad incidente sobre la frontera inferior, la (7.20) permite expresar la
intensidad de un rayo emergente por la frontera superior, normal a la capa ( = 1), de la
siguiente manera :
150
T
I (0,1) =
 Se
 t
dt  S (1  e T )
0
Si T  1, resulta directamente I(0,1) = S. Es decir, si la función fuente es
constante en una capa de espesor finito ópticamente gruesa (T  1) sobre la cual no
incide radiación por la frontera inferior, la intensidad específica monocromática que
emerge normalmente de dicha capa es igual a la misma función fuente.
Para interpretar físicamente la solución (7.19) en el caso de una atmósfera semiinfinita tomaremos  1 = 0 y haremos tender  2 a infinito. El primer término de la
solución general (7.19) desaparece en este caso en virtud de la condición límite
impuesta en (7.14). En consecuencia, se tendrá ahora :
I (0,) =

 S (t )e
t / 
0
dt
(7.21)

Si sólo se consideran valores de  positivos (radiación emergente), la fórmula
anterior expresa el hecho de que la intensidad emergente de una atmósfera semi-infinita
en una dirección , está dada por la suma sobre todas las profundidades ópticas t de las
intensidades generadas en cada profundidad t correspondientemente atenuadas por el
factor e  t /  .
La ecuación (7.21) constituye la forma integral básica de la ecuación del
transporte radiativo. Si pudiésemos resolver esta ecuación estaríamos en condiciones de
expresar lo que predice la teoría. Sin embargo, para efectuar la integración en (7.21)
debemos conocer de qué manera varía la función fuente con la profundidad óptica .
Hemos visto en la Sección 6.10 que en ciertos casos S se reduce a funciones simples
tales como B(,T) o J. En ocasiones, sin embargo, S puede resultar una función muy
complicada.
A manera de ejemplo ilustrativo, calcularemos la intensidad específica
monocromática emergente de una atmósfera semi-infinita caracterizada por una función
fuente lineal de la forma :
S (t) = a + bt
(7.22)
Reemplazando (7.22) en (7.21) resulta :

I(0,) = a  e  t / 
0
dt


 b  t e  t / 
0
Haciendo el cambio de variables x = t/, se obtiene :
dt

151


I(0,) = a  e dx  b  xe  x dx
x
0
(7.23)
0
La primera de las integrales del segundo miembro es obviamente la unidad, en
tanto que la segunda puede resolverse “por partes”, llamando  = x y dv = e-x. Dado que
con esta sustitución d = dx y v = e-x, resulta :

x
x
 xe dx   xe

0
0

  e x dx
0
El primer término del segundo miembro se anula ya que al aplicar la regla de
L’Hópital resulta :
lim
x 
-
x

ex
lim
x 
-
1
0
ex
Por lo tanto, si S es una función lineal de la profundidad óptica, la intensidad
específica monocromática emergente de la atmósfera semi-infinita resulta una función
lineal de la variable  :
I(0,) = a + b
(7.24)
En general, para resolver el problema es necesario conocer la función fuente lo
que no siempre es posible.
Consideremos ahora un punto arbitrario interior a una atmósfera semi-infinita,
ubicado a una profundidad óptica . Supondremos que no incide radiación sobre la
superficie de la atmósfera y admitiremos además que es válida la condición de contorno
(7.14). La intensidad I(,) resultante en el punto a profundidad óptica  y en la
dirección considerada debe ser la suma algebraica de las intensidades emergente
I em () e incidente I in () en ese punto, según la dirección considerada (Figura 7-8).
Obviamente,  será positivo y negativo en uno y otro caso, respectivamente.
152
frontera
superior
I em
v ( ,  )

observador
I inv (,  )
 = 0
Figura 7-8: Intensidad específica monocromática
resultante en un punto interior de una atmósfera semiinfinita.
Consideremos en primer lugar la radiación emergente del punto considerado. Si el
ángulo  se mide como indica la Figura 7-8, la radiación emergente corresponde a los
valores angulares comprendidos en el intervalo 3/2 <   /2, o bien 0 <   1. Para
poder aplicar la solución general (7.19) consideraremos  1 =  y haremos tender  2 a
infinito. En ese caso, teniendo en cuenta (7.14), resulta :
I (,) =
em


 S (t )e


 ( t   ) / 
dt

,
(7.25)
válida para los rayos comprendidos en el intervalo 0 <   1.
Pero el punto considerado también recibe radiación puesto que no se encuentra
sobre la frontera superior. Considerando ahora  1 =  y  2 = 0, la radiación
incidente resulta de (7.19) de la siguiente manera :
153
I (,) =
in

0
 S (t )e

 ( t   ) / 

dt

,
(7.26)
válida para los rayos comprendidos en el intervalo –1   < 0.
La solución completa de la ecuación del transporte radiativo en un punto
cualquiera de una atmósfera estelar semi-infinita, de capas plano-paralelas, estará dada
por la suma de (7.25) y (7.26) :
I(,) =

 S (t )e

 ( t  ) / 

dt

0
  S (t )e (t  ) / 

dt

(7.27)
Debe tenerse en cuenta que el primer término de la expresión anterior es válido
para 0 <   1, en tanto que el segundo es válido para –1   < 0. Al igual que antes,
para poder conocer la intensidad específica monocromática en un punto cualquiera de
una fotosfera es necesario conocer la función fuente.
Al considerar el caso particular de la atmósfera semi-infinita, lo que en verdad nos
interesa es poder predecir teóricamente cuál es la intensidad específica monocromática
emergente en una cierta dirección. Este resultado, obtenido en (7.21), es muy importante
porque nos permite efectuar comparaciones con las observaciones de la superficie solar.
No debemos perder de vista que estamos suponiendo que el transporte de energía es
sólo radiativo y que las capas fotosféricas son plano-paralelas.
La (7.21) es una ecuación integral relativamente simple. Lamentablemente, en la
mayoría de los casos S es una función bastante complicada. Si la función fuente S está
dada por la expresión (6.62) puede considerarse relativamente simple, pero aún así
existen problemas para conocer el campo radiativo porque S depende de J, la que a su
vez depende del campo radiante I. Estamos pues dentro de un círculo vicioso, motivo
por el cual construiremos de otra manera los modelos de atmósferas estelares.
7.6 INTEGRALES EXPONENCIALES
Introduciremos ahora el concepto matemático de integral exponencial, el cual
resultará de suma utilidad no sólo para simplificar los cálculos, sino también para
clarificar la interpretación de ciertas expresiones que deduciremos en la siguiente
sección.
Se define la integral exponencial de orden n como una integral impropia de la
siguiente manera :

En(x) =
e xt
1 t n dt ,
(7.28)
154
en la cual n debe ser un número entero mayor o igual que la unidad. Una vez fijado el
parámetro n, la integral En(x) resulta una función estrictamente decreciente de la
variable x. De la definición resulta en forma inmediata el valor de la integral
exponencial de orden n en el origen (x = 0) :
En(0) =
1
( n  1)
(7.29)
Luego: E1(0) = , E2(0) = 1, E3(0) = 1/2, E4(0) = 1/3, etc. Además, de (7.28) se
desprende que para valores suficientemente grandes de la variable x, las integrales
exponenciales tienden a anularse, cualquiera sea el orden de n. La forma de las
integrales exponenciales se ilustra en la Figura (7-9).
En(x)
n=1
1.0
n=2
0.5
n=3
n=4
0.4
0.8
1.2
1.6
2.0
X
Figura 7-9: Integrales exponenciales para distintos valores del parámetro n
Existen fórmulas de recurrencia que permiten hallar las integrales exponenciales
En(x) conociendo las integrales exponenciales En+1(x), o viceversa. En particular, resulta
sencillo demostrar la siguiente relación de recurrencia :
n En+(x) = e-x – x En(x)
(7.30)
Además, si se deriva la expresión (7.28) con respecto a x, se obtiene la siguiente
relación simple entre En(x) y En-1(x) :
155
dE n ( x )
 E n 1 ( x )
dx
(7.31)
Abramowitz y Stegun (1964) encontraron muy buenas aproximaciones para el
cálculo de la integral exponencial de primer orden. Dichas expresiones son las
siguientes :
E1(x) = - ln x – 0.57721566 + 0.99999193 x – 0.24991055 x2 + 0.05519968 x3 –
-0.00976004 x4 + 0.0010785 x5,
válida para x  1.
E1(x) =
x 4  a1 x 3  a2 x 2  a3 x  a4 1
,
.
x 4  b1 x 3  b2 x 2  b3 x  b4 xe x
válida para x > 1, donde :
a1 = 8.5733287401
a2 = 18.0590169730
a3 = 8.6347608925
a4 = 0.2677737343
b1 = 9.5733223454
b2 = 25.6329561486
b3 = 21.0996530827
b4 = 3.9584969228
Las expresiones polinómicas obtenidas por los mencionados autores permiten
calcular la integral exponencial E1(x) con un error menor que 2x10-7.
7.7 EXPRESIÓN TEÓRICA DEL FLUJO
Nos proponemos a continuación obtener una expresión teórica de la densidad de
flujo de radiación, o simplemente el flujo, en cualquier punto de una atmósfera estelar
semi-infinita. Si admitimos que la estrella tiene simetría esférica, I no depende del
ángulo acimutal . En consecuencia, la expresión (6.16) permite escribir el flujo
monocromático en la profundidad óptica  de la atmósfera de la siguiente manera :
F() = 2
 /2

0
Iem cos send  2

 I

in
cos send
(7.32)
/2
Si se elige un elemento de área en la atmósfera normal al radio de la estrella y la
dirección radial corresponde a  = 00, entonces los dos términos del segundo miembro
en (7.32) representan los flujos emergente e incidente, respectivamente. Reemplazando
156
las intensidades emergente e incidente por sus respectivas expresiones (7.25) y (7.26),
resulta :
F() = 2
 /2 
  S (t )e
0
 ( t   ) sec 
sendt d  2
 
  S (t )e

 ( t   ) sec 
sendt d
/2 0

Si suponemos además que la función fuente S no depende del ángulo 
(condición de isotropía), se obtiene la siguiente expresión teórica del flujo :
F() = 2

 /2

0
 S (t )  e

 ( t  ) sec 


0
 /2
sen ddt - 2  S (t )  e (t  ) sec  senddt
Esta expresión puede simplificarse usando integrales exponenciales y efectuando
cambios de variables apropiados. En efecto, si en el primer término se hace la
sustitución :  = sec , x = (tv - v), se obtiene en forma inmediata que sen d =
d/2. La primera integral con variable angular resulta entonces :
 /2
 ( t  ) sec 
 e v v sen d =
0

e  x

2
d = E2(x)
(7.33)
1
Análogamente, haciendo las sustituciones ’ = - sec, y = (v – tv), se obtiene
que send = - d’/’2 y la segunda integral angular de la expresión teórica del flujo
resulta :

 ( t  ) sec 
 e v v sen =
 /2

e y '
1  '2 d’ = E2(y)
(7.34)
Conviene aclarar en este último caso que cuando la variable  tiende a /2, la
nueva variable ’ tiende a +. Esto es así debido a que cuando  tiende a /2 lo hace
viniendo desde  =  y, por ende, el cos tiende a cero por valores negativos. En
consecuencia, ’= 1/cos tiende a +.
Teniendo en cuenta (7-33) y (7-34) la expresión teórica del flujo queda :
Fv(v) = 2


v
Sv(t)E2(tv-v)dtv - 2
v

0
Sv(t)E2(v-tv) dtv,
(7.35)
157
la cual se conoce como integral del flujo o ecuación integral de Milne.
La expresión obtenida es de gran importancia ya que contrariamente a la
intensidad específica, el flujo constituye un parámetro que puede ser observado en todos
los objetos astronómicos. En realidad, las observaciones permiten conocer el flujo en la
superficie estelar. Por lo tanto, el flujo teórico a comparar con las observaciones será el
dado por (7-35) pero para v = 0, esto es :
Fv(0) = 2


Sv(tv) E2(tv) dtv
(7.36)
0
El flujo superficial teórico está pues compuesto de la suma sobre todas las
profundidades ópticas contribuyentes, de la función fuente en cada punto, atenuada por
el correspondiente factor de extinción. Debe tenerse en cuenta que el flujo superficial
expresado en (7-36), representa la energía por unidad de tiempo e intervalo de
frecuencia que teóricamente atraviesa un elemento de área ubicado sobre la superficie
de la estrella. El flujo monocromático total emitido teóricamente por la estrella resulta
de multiplicar (7-36) por la superficie total de la estrella. Si no existe absorción de la
radiación entre la estrella y la tierra, llamando fv a la cantidad de energía por unidad de
tiempo (flujo) que se recibe en la tierra (fuera de la atmósfera), por unidad de área e
intervalo de frecuencia, por conservación de la energía se tendrá :
4R2Fv(0) = 4r2fv ,
(7.37)
en la cual r es la distancia tierra-estrella y R el radio de la estrella supuesta esférica. En
la práctica, cuando se conocen R y r, suelen compararse las cantidades medidas fv para
diferentes rangos de frecuencia, con los correspondientes valores teóricos (R/r)2Fv(0)
calculados de (7-37), usando una determinada función fuente.
7.8 INTENSIDAD MEDIA E INTEGRAL K EN FUNCIÓN DE INTEGRALES
EXPONENCIALES
Expresiones semejantes a la del flujo teórico pueden encontrarse para la
intensidad media Jv(v) y la integral K. Si se supone que Iv no depende del ángulo
acimutal , las expresiones (6.8) y (6.29) conducen a las siguientes:
Jv(v) =
1
Kv(v) =
2
 /2
1
2
 /2
0
(7.38)
1 in
I v (v,) cos2 sen d

2  /2
(7.39)
0
em
 I v (v,) cos2 sen d +

1 in
I v (v,) sen d ,
2 / 2
em
 I v (v,) sen d +

158
Reemplazando I em
e I inv por las respectivas expresiones dadas en (7.25) y (7.26),
v
suponiendo que Sv es isotrópica y efectuando los mismos cambios de variables que
antes, se obtienen las siguientes expresiones :


Jv(v) =
1 v
1
S
(t
)
E
(t

)
dt
+
Sv E1(v-tv) dtv,

v
1 v v
v
2 0
2 v
Kv(v) =
1 v
1
S
(t
)
E
(t

)
dt
+
Sv(t) E3(v-tv) dtv,
v 
3 v v
v
2 0
2 v

(7.40)

(7.41)
de las cuales la primera se conoce como ecuación integral de Schwarzschild-Milne.