Funciones cuadráticas o parábolas
Anuncio
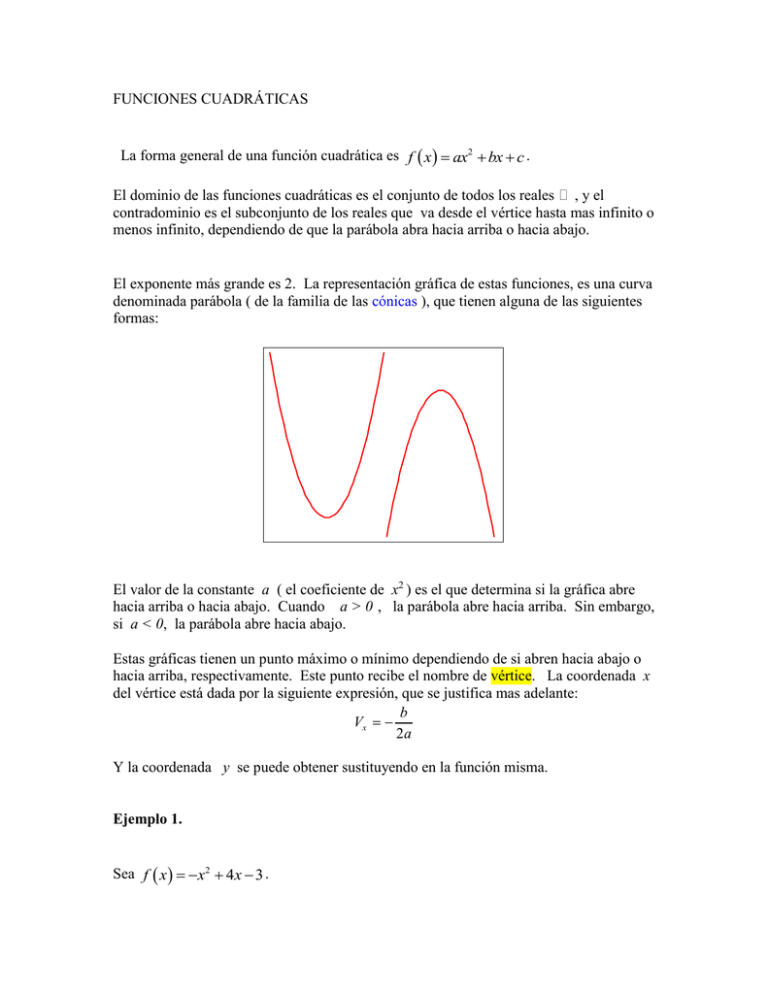
FUNCIONES CUADRÁTICAS La forma general de una función cuadrática es f x ax2 bx c . El dominio de las funciones cuadráticas es el conjunto de todos los reales , y el contradominio es el subconjunto de los reales que va desde el vértice hasta mas infinito o menos infinito, dependiendo de que la parábola abra hacia arriba o hacia abajo. El exponente más grande es 2. La representación gráfica de estas funciones, es una curva denominada parábola ( de la familia de las cónicas ), que tienen alguna de las siguientes formas: El valor de la constante a ( el coeficiente de x2 ) es el que determina si la gráfica abre hacia arriba o hacia abajo. Cuando a > 0 , la parábola abre hacia arriba. Sin embargo, si a < 0, la parábola abre hacia abajo. Estas gráficas tienen un punto máximo o mínimo dependiendo de si abren hacia abajo o hacia arriba, respectivamente. Este punto recibe el nombre de vértice. La coordenada x del vértice está dada por la siguiente expresión, que se justifica mas adelante: b Vx 2a Y la coordenada y se puede obtener sustituyendo en la función misma. Ejemplo 1. Sea f x x2 4x 3 . Una representación tabular de esta función es la siguiente: x -1 0 1 2 3 4 5 f(x) -8 -3 0 1 0 -3 -8 En este caso las constantes son: a = -1, b = 4, c = -3. Esta parábola abre hacia abajo dado que a 1 ; su vértice es el punto máximo, cuya coordenada x es: Vx b 4 4 2 2a 2 1 2 En la representación tabular vemos que a este valor de x le corresponde f 2 2 4 2 3 2 4 8 3 1 Por lo que el vértice de la parábola es el punto ( 2, 1 ). Al igual que en la recta, el término independiente indica el punto donde la parábola intersecta al eje y. En esta función es el punto (0,-3). La representación gráfica de esta función, obtenida de la tabla es: El dominio de esta función es ( , ) y el contradominio es ( , 1] . Como se puede ver en la figura, esta parábola cruza el eje x en dos puntos, esto es, tiene dos raíces. Al igual que con la función lineal, para encontrar las raíces se resuelve la ecuación f ( x) 0 : f x x2 4x 3 0 x2 4 x 3 A diferencia de las funciones lineales, no se puede despejar directamente; por lo tanto, se factoriza cuando es posible, o se utiliza la fórmula general comúnmente llamada chicharronera: x En este caso: b b2 4ac 2a x 4 4 2 4 1 3 2 1 4 16 12 4 2 2 2 4 2 1 2 4 2 3 2 Las raíces son x = 1 y x = 3 . Note que 2 2 b 4ac (4) 4(1)(3) 16 12 4 0 , conocido como discriminante, en este caso es positivo. Ejemplo 2. Sea la función f x x2 16 , hallar sus raíces. Hay por lo menos tres alternativas para obtener las raíces: En un primer caso, se puede factorizar como f x x 4 x 4 . Para encontrar las raíces se iguala a cero x 4 x 4 0 lo que se cumple sólo cuando x = 4 y x = -4. Como en esta función la constante b = 0 , una segunda opción es despejar: x 2 16 0 x 2 16 x 16 4 Finalmente, siempre se puede recurrir a la fórmula general: x 0 02 4 1 16 2 1 64 4 . 2 Ejemplo 3. Sea f x x2 6x 9 . Encontrar sus raíces y graficar. Observe que x2 6 x 9 es un trinomio cuadrado perfecto, por lo que la función se 2 puede escribir f x x 3 . Para encontrar las raíces igualamos a cero y resolvemos: x 3 0 x 3 ( x 3) 0 2 Esto se cumple sólo cuando x 3 . Existe una sola raíz, que se repite; se dice que es una raíz de multiplicidad 2. Si calculamos el discriminante b2 4ac (6)2 4(1)(9) 36 36 0 , notamos que, en este caso es igual a cero. Las coordenadas del vértice de la parábola son: Vx 6 3 2 1 f 3 3 3 0 2 V 3, 0 para trazar la gráfica se necesitan al menos dos puntos mas: x -4 -2 f(x) 1 1 10 9 8 7 6 5 4 3 2 1 0 -6 -5 -4 -3 -2 -1 -1 0 El dominio de esta función es ( , ) y el contradominio es [ 0, ) . Ejemplo 4. Sea la función f x x2 4 , hallar las raíces y graficar. Despejando directamente: x2 4 0 x 2 4 x 4 Se obtienen dos raíces imaginarias. Si calculamos el discriminante b2 4ac (0)2 4(1)(4) 16 0 , notamos que, en este caso es negativo. Las coordenadas del vértice son: Vx 0 0 2 1 f 0 02 4 4 la parábola abre hacia abajo, y dado que el vértice V( 0, -4 ) está abajo del eje x, la gráfica no cruza este eje. 5 0 -3 -2 -1 0 1 2 3 -5 -10 -15 Observe que, en este caso, la intersección con el eje y coincide con el vértice. Ejemplo 5. Sea f ( x) x2 5 . Hallar las raíces. Después de igualar a cero se puede despejar directamente x2 5 0 x2 5 x 5 Recuerde que 5 2.236068... es un número irracional. Las coordenadas del vértice son: Vx 0 0 2 1 f 0 02 5 5 Con estos tres puntos se puede trazar la gráfica. RESUMEN Forma general Mayor exponente de la x Función constante f ( x) c 0 Función lineal Función cuadrática f ( x) mx b f ( x) ax2 bx c 1 2 2 cruces, si b 2 4ac 0 (dos raíces reales) Número de veces que cruza el eje x (raíces) Número de veces que cruza el eje y : ordenada al origen Características generales de la gráfica 0 1 1, si m 0 1 1 cruce, si b 2 4ac 0 (una raíz real con multiplicidad) 0 cruces, si b 2 4ac 0 (dos raíces complejas) 1 Esto es requisito para que sea función. Si para un mismo valor de x hay más de un valor de f(x), entonces, no es una función. es una línea horizontal es creciente cuando m 0 y decreciente cuando m 0 abre hacia arriba cuando a 0 y hacia abajo cuando a 0 Como se puede observar en la tabla anterior, el número de raíces es igual al exponente máximo de la x.
