segundo practico alumnos
Anuncio
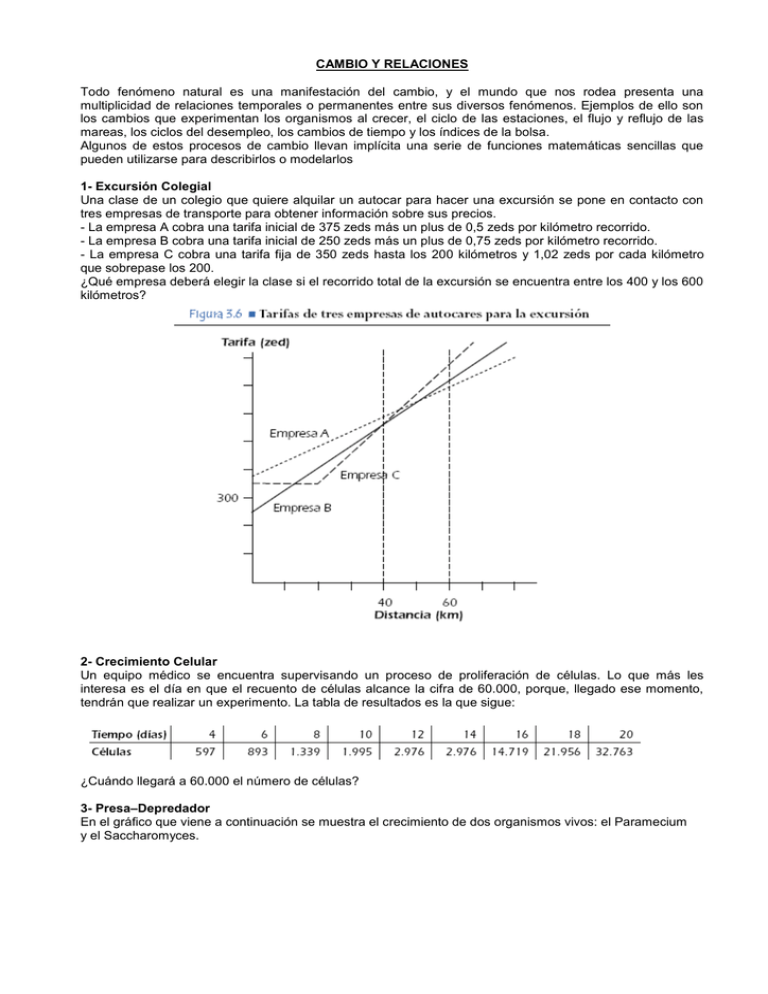
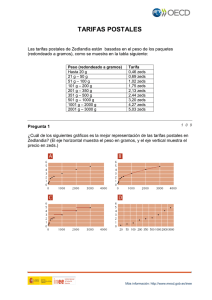
CAMBIO Y RELACIONES Todo fenómeno natural es una manifestación del cambio, y el mundo que nos rodea presenta una multiplicidad de relaciones temporales o permanentes entre sus diversos fenómenos. Ejemplos de ello son los cambios que experimentan los organismos al crecer, el ciclo de las estaciones, el flujo y reflujo de las mareas, los ciclos del desempleo, los cambios de tiempo y los índices de la bolsa. Algunos de estos procesos de cambio llevan implícita una serie de funciones matemáticas sencillas que pueden utilizarse para describirlos o modelarlos 1- Excursión Colegial Una clase de un colegio que quiere alquilar un autocar para hacer una excursión se pone en contacto con tres empresas de transporte para obtener información sobre sus precios. - La empresa A cobra una tarifa inicial de 375 zeds más un plus de 0,5 zeds por kilómetro recorrido. - La empresa B cobra una tarifa inicial de 250 zeds más un plus de 0,75 zeds por kilómetro recorrido. - La empresa C cobra una tarifa fija de 350 zeds hasta los 200 kilómetros y 1,02 zeds por cada kilómetro que sobrepase los 200. ¿Qué empresa deberá elegir la clase si el recorrido total de la excursión se encuentra entre los 400 y los 600 kilómetros? 2- Crecimiento Celular Un equipo médico se encuentra supervisando un proceso de proliferación de células. Lo que más les interesa es el día en que el recuento de células alcance la cifra de 60.000, porque, llegado ese momento, tendrán que realizar un experimento. La tabla de resultados es la que sigue: ¿Cuándo llegará a 60.000 el número de células? 3- Presa–Depredador En el gráfico que viene a continuación se muestra el crecimiento de dos organismos vivos: el Paramecium y el Saccharomyces. Uno de los dos animales (el depredador) se come al otro (la presa). ¿Permite el gráfico identificar cuál es la presa y cuál el depredador? Una propiedad del fenómeno presa–depredador se puede expresar de la siguiente manera: la tasa de crecimiento de los depredadores es proporcional a la cantidad de presas disponibles. ¿Es aplicable esta propiedad al gráfico anterior? 4- Caminar La foto muestra las huellas de un hombre caminando. La longitud del paso P es la distancia entre los extremos posteriores de dos huellas consecutivas. Para los hombres, la fórmula n 140 da una relación aproximada entre n y P donde: P n = número de pasos por minuto, y P = longitud del paso en metros. a- Si se aplica la fórmula a la manera de caminar de Enrique y éste da 70 pasos por minuto, ¿cuál es la longitud del paso de Enrique? Muestra tus cálculos. b- Bernardo sabe que sus pasos son de 0,80 metros. El caminar de Bernardo se ajusta a la fórmula. Calcula la velocidad a la que anda Bernardo en metros por minuto y en kilómetros por hora. Muestra tus cálculos. 5- Crecer La juventud se hace más alta. La estatura media de los chicos y las chicas de Holanda en 1998 está representada en el siguiente gráfico. a- Desde 1980 la estatura media de las chicas de 20 años ha aumentado 2,3 cm, hasta alcanzar los 170,6 cm. ¿Cuál era la estatura media de las chicas de 20 años en 1980? b- Explica cómo está reflejado en el gráfico que la tasa de crecimiento de la estatura media de las chicas disminuye a partir de los 12 años en adelante. c- De acuerdo con el gráfico anterior, como promedio, durante qué periodo de su vida son las chicas más altas que los chicos de su misma edad. 6- Zapatos para niños La siguiente tabla muestra las tallas de zapato recomendadas en Zedlandia para las diferentes longitudes de pie. a- El pie de Marina mide 163 mm de longitud. Utiliza la tabla para determinar cuál es la talla de zapatos de Zedlandia que Marina debería probarse. 7- El mejor Coche Una revista de coches utiliza un sistema de puntuaciones para evaluar los nuevos coches y concede el premio de Mejor coche del año al coche con la puntuación total más alta. Se están evaluando cinco coches nuevos. Sus puntuaciones se muestran en la tabla. Las puntuaciones se interpretan de la siguiente manera: 3 puntos = Excelente 2 puntos = Bueno 1 punto = Aceptable a- Para calcular la puntuación total de un coche, la revista utiliza la siguiente regla, que da una suma ponderada de las puntuaciones individuales: Puntuación total = (3× S) + C + D + H Calcula la puntuación total del coche Ca. Escribe tu contestación en el espacio siguiente. Puntuación total de Ca: . . . . . . . . . . . . . . . . . . . . b- El fabricante del coche Ca pensó que la regla para obtener la puntuación total no era justa. Escribe una regla para calcular la puntuación total de modo que el coche Ca sea el ganador. Tu regla debe incluir las cuatro variables y debes escribir la regla rellenando con números positivos los cuatro espacios de la ecuación siguiente. Puntuación total = ……… S + ……… C + ……… D + ……… H. 8- Exportaciones Estos gráficos contienen información sobre las exportaciones de Zedlandia, un país cuya unidad monetaria es el zed. a- ¿Cuál fue el valor de las exportaciones de zumos de fruta de Zedlandia en 2000? b- ¿Cuál fue el valor de las exportaciones de zumo de fruta de Zedlandia en el año 2000? 9- Distancia María vive a dos kilómetros del colegio y Martín a cinco. ¿A qué distancia viven el uno del otro? 10- La Pizza Una pizzería ofrece dos pizzas redondas del mismo grosor en diferentes tamaños. La pequeña tiene 30 cm de diámetro y cuesta 30 zeds. La grande tiene 40 cm de diámetro y cuesta 40 zeds. ¿Qué pizza es la mejor opción en relación con su coste? Escribe tu razonamiento. 11- El Faro Los faros son torres que disponen de un foco luminoso en su parte superior. Los faros ayudan a los barcos a seguir su rumbo de noche cuando navegan cerca de la costa. Un faro emite destellos luminosos según una secuencia regular fija. Cada faro tiene su propia secuencia. En el diagrama que figura a continuación puede verse la secuencia de un determinado faro. Los destellos de luz alternan con períodos de oscuridad. Se trata de una secuencia regular. Al cabo de un tiempo, la secuencia se vuelve a repetir. El tiempo que tarda en completarse un ciclo completo, antes de volver a iniciarse la secuencia, recibe el nombre de período. Una vez que se ha hallado el período de la secuencia es fácil ampliar el diagrama para los siguientes segundos, minutos e incluso horas. Realiza un gráfico en el diagrama de abajo, indicando una secuencia posible de destellos de un faro que emita destellos durante 30 segundos por minuto. El período de esta secuencia debe ser igual a 6 segundos. 12- La Foca Las focas tienen que subir a la superficie para respirar, incluso cuando están dormidas. Martín ha estado observando a una foca durante una hora. Al empezar la observación, la foca se sumergió hasta el fondo del mar y se puso a dormir. A los 8 minutos, ascendió flotando lentamente hasta la superficie y tomó aire. 3 minutos después se encontraba de nuevo en el fondo y todo el proceso volvió a iniciarse de un modo sumamente regular. Transcurrida una hora, la foca estaba: A. En el fondo B. De camino hacia la superficie C. Respirando D. De camino hacia el fondo 13- Indonesia Indonesia se encuentra entre Malasia y Australia. La tabla que viene a continuación contiene algunos datos sobre la población de Indonesia y sobre su distribución en las distintas islas que la componen. Uno de los principales retos que tiene planteados Indonesia es la distribución desigual de su población en sus distintas islas. Como puede verse en la tabla, Java, que ocupa menos del 7 % de la superficie total, tiene casi el 62 % de la población. Diseña un gráfico (o gráficos) en que se muestre la distribución desigual de la población Indonesia. 14- Canales De Riego A continuación se presenta un esquema de un sistema de canales de riego para zonas de regadío. Las compuertas, de la A a la H se pueden abrir y cerrar para dejar que el agua vaya allí donde se necesite. Cuando una compuerta se cierra, el agua no puede pasar por ella. El problema que se plantea es encontrar una compuerta que está atascada y que impide que el agua fluya a través del sistema de canales. a- Miguel se da cuenta que el agua no siempre va a donde se supone que tiene que ir. Piensa que una de las compuertas está atascada, de modo que, cuando se le envía la orden de abrir, no se abre. Miguel utiliza la configuración de órdenes de la Tabla 1 para comprobar las compuertas. Tabla 1: A B C D E F G H Abierta Cerrada Abierta Abierta Cerrada Abierta Cerrada Abierta Con la configuración de órdenes para las compuertas que se muestra en la Tabla 1, dibujá en el diagrama todos los caminos posibles de flujo del agua. Suponé que todas las compuertas funcionan según la configuración de órdenes anterior. b- Miguel desea poder examinar si la compuerta D está atascada. Confeccioná una tabla con la configuración de órdenes para las compuertas, para verificar si la compuerta D está atascada cuando está configurada como abierta. Configuración de órdenes para las compuertas (escribe para cada una de ellas abierta o cerrada) 15- Manzanos Y Coníferas Un agricultor planta manzanos en un terreno cuadrado. Con el objeto de proteger los manzanos del viento planta coníferas alrededor de la totalidad del huerto. Aquí ves un esquema de esta situación donde se puede apreciar la colocación de los manzanos y de las coníferas para cualquier número(n) de filas de manzanos: a- Completá la tabla: n 1 2 3 4 5 número manzanos de número coníferas de b- Supongamos que el agricultor quiere plantar un huerto mucho mayor, con muchas filas de árboles. A medida que el agricultor vaya haciendo mayor el tamaño del huerto, qué aumentará más rápidamente: el número de manzanos o el número de coníferas? Explicá cómo llegaste a tu respuesta. 16- Horarios Mark (de Sydney, Australia) y Hans (de Berlín, Alemania) se comunican a menudo a través de Internet mediante el chat. Tienen que conectarse a Internet a la vez para poder “chatear”. Para encontrar una hora apropiada para chatear, Mark buscó un mapa horario mundial y halló lo siguiente: a- Cuando son las 7:00 de la tarde en Sydney, ¿qué hora es en Berlín? b- Mark y Hans no pueden chatear entre las 9:00 de la mañana y las 4:30 de la tarde, de sus respectivas horas locales, porque tienen que ir al colegio. Tampoco pueden desde las 11:00 de la noche hasta las 7:00 de la mañana, de sus respectivas horas locales, porque estarán durmiendo. ¿A qué horas podrían chatear Mark y Hans? Escribí las respectivas horas locales. 17-Equivalencias Si m representa un número positivo, ¿a qué es equivalente m + m + m + m? A m+4 B 4m C m4 D 4(m + 1) 18- Gráficos En una gráfica, una recta pasa por los puntos (3,2) y (4,4). ¿Cuál de los siguientes puntos está también en esa recta? A (1,1) B (2,4) C (5,6) D (6,3) E (6,5) 19-Plan De Estudios Una escuela técnica ofrece las siguientes 12 asignaturas para una carrera de 3 años en la que la duración de cada asignatura es de un año: Código de la Nombre de la asignatura asignatura 1 M1 Mecánica. Nivel 1 2 M2 Mecánica. Nivel 2 3 E1 Electrónica. Nivel 1 4 E2 Electrónica. Nivel 2 5 B1 Estudios empresariales. Nivel 1 6 B2 Estudios empresariales. Nivel 2 7 B3 Estudios empresariales. Nivel 3 8 C1 Sistemas de ordenadores. Nivel 1 9 C2 Sistemas de ordenadores. Nivel 2 10 C3 Sistemas de ordenadores. Nivel 3 11 T1 Gestión de Tecnología e Información. Nivel 1 12 T2 Gestión de Tecnología e Información. Nivel 2 Cada estudiante cursará 4 asignaturas por año para así aprobar 12 asignaturas en 3 años. Un estudiante sólo puede cursar una asignatura de nivel superior si ha aprobado el año anterior la misma asignatura del nivel o niveles inferiores. Por ejemplo, sólo se puede cursar Estudios Empresariales de Nivel 3 después de haber aprobado Estudios Empresariales de Nivel 1 y Nivel 2. Además, sólo puede elegirse Electrónica de Nivel 1 después de aprobar Mecánica de Nivel 1, y sólo puede elegirse Electrónica de Nivel 2 después de aprobar Mecánica de Nivel 2. Completa la siguiente tabla con las asignaturas que deberían ofrecerse en cada curso. Escribe en la tabla los códigos de cada asignatura. Curso Asignatura 1 Asignatura 2 Asignatura 3 Asignatura 4 1er curso 2o curso 3er curso 20- Vacaciones En este problema se trata de planificar la mejor ruta para unas vacaciones. En las Figuras A y B se muestra un mapa de la zona y las distancias entre las distintas poblaciones a- Calcula la distancia más corta por carretera entre Nuben y Kado. b- Zoe vive en Angaz y quiere visitar Kado y Lapat. La distancia máxima que puede recorrer en un mismo día son 300 kilómetros, pero tiene la posibilidad de acampar durante la noche en cualquier punto situado entre las distintas poblaciones. Zoe pasará dos noches en cada una de las poblaciones para así poder dedicar un día entero a visitar cada una de ellas. Completa la tabla que viene a continuación con el itinerario de Zoe, indicando dónde pasa cada una de la noches. 21- Velocidad de un Auto de Carrera a- ¿Cuál es la distancia aproximada desde la línea de partida hasta el comienzo del tramo recto mas largo de la pista? b- ¿ dónde se registró la velocidad mas baja durante la segunda vuelta? c- ¿ Qué se puede decir sobre la velocidad del auto entre el km 2.6 y el km 2.8? d- Aquí hay cinco pistas dibujadas: ¿sobre cuál de estas pistas se desplazó el auto para producir el gráfico de velocidad mostrado anteriormente? 22- Frecuencia Cardíaca Por motivos de salud se recomienda que, al realizar un esfuerzo, la práctica de un deporte, por ejemplo, no se exceda de una determinada frecuencia cardíaca. Durante muchos años, la relación entre la máxima frecuencia cardíaca recomendada y la edad del individuo se describió mediante la siguiente fórmula: Máxima frecuencia cardíaca recomendada = 220 – edad Las últimas investigaciones, sin embargo, indican que esta fórmula debe ser modificada ligeramente. La nueva fórmula es la siguiente: Máxima frecuencia cardíaca recomendada = 208 – (0,7 x edad) ¿ puedes decir qué diferencias encuentras entre ambas fórmulas y el modo en que éstas afectan al cálculo de la máxima frecuencia cardíaca recomendada?