PROBLEMA: Dado el sistema de la siguiente figura, ajuste el valor... para que el margen de fase del sistema sea de...

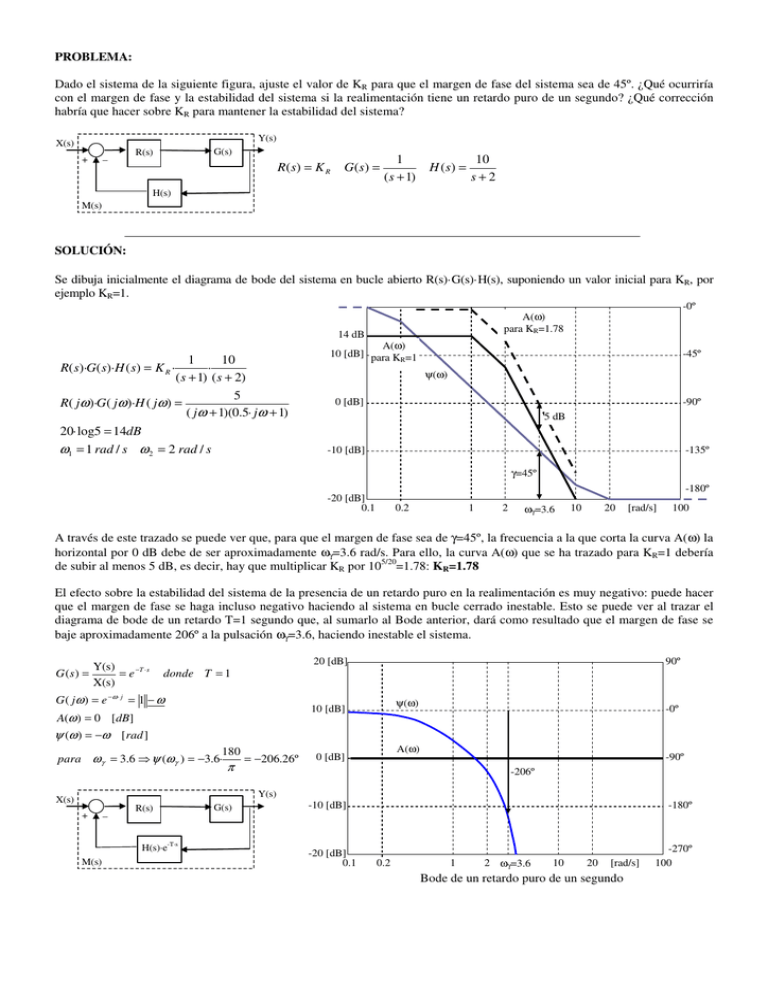
PROBLEMA:
Dado el sistema de la siguiente figura, ajuste el valor de KR para que el margen de fase del sistema sea de 45º. ¿Qué ocurriría
con el margen de fase y la estabilidad del sistema si la realimentación tiene un retardo puro de un segundo? ¿Qué corrección
habría que hacer sobre KR para mantener la estabilidad del sistema?
Y(s)
X(s)
_
+
G(s)
R(s)
R ( s) = K R
G(s) =
1
( s + 1)
H (s) =
10
s+2
H(s)
M(s)
SOLUCIÓN:
Se dibuja inicialmente el diagrama de bode del sistema en bucle abierto R(s)·G(s)·H(s), suponiendo un valor inicial para KR, por
ejemplo KR=1.
-0º
A(ω)
para KR=1.78
14 dB
1
10
·
( s + 1) (s + 2)
5
R( jω )·G( jω )·H ( jω ) =
( jω + 1)(0.5· jω + 1)
20·log5 = 14dB
R( s)·G( s)·H ( s) = K R ·
ω1 = 1 rad / s ω 2 = 2 rad / s
A(ω)
10 [dB] para KR=1
-45º
ψ(ω)
0 [dB]
-90º
5 dB
-10 [dB]
-135º
γ=45º
-180º
-20 [dB]
0.1
0.2
1
2
ωγ=3.6
10
20
[rad/s]
100
A través de este trazado se puede ver que, para que el margen de fase sea de γ=45º, la frecuencia a la que corta la curva A(ω) la
horizontal por 0 dB debe de ser aproximadamente ωγ=3.6 rad/s. Para ello, la curva A(ω) que se ha trazado para KR=1 debería
de subir al menos 5 dB, es decir, hay que multiplicar KR por 105/20=1.78: KR=1.78
El efecto sobre la estabilidad del sistema de la presencia de un retardo puro en la realimentación es muy negativo: puede hacer
que el margen de fase se haga incluso negativo haciendo al sistema en bucle cerrado inestable. Esto se puede ver al trazar el
diagrama de bode de un retardo T=1 segundo que, al sumarlo al Bode anterior, dará como resultado que el margen de fase se
baje aproximadamente 206º a la pulsación ωγ=3.6, haciendo inestable el sistema.
G (s) =
Y(s)
= e −T · s
X(s)
20 [dB]
90º
donde T = 1
G ( jω ) = e −ω · j = 1 − ω
ψ(ω)
10 [dB]
A(ω ) = 0 [dB]
-0º
ψ (ω ) = −ω [ rad ]
180
para ωγ = 3.6 ⇒ ψ (ωγ ) = −3.6·
= −206.26º
A(ω)
0 [dB]
-90º
π
-206º
Y(s)
X(s)
+
_
R(s)
H(s)·e-T·s
M(s)
G(s)
-10 [dB]
-20 [dB]
0.1
-180º
0.2
1
2 ωγ=3.6
10
20
[rad/s]
Bode de un retardo puro de un segundo
-270º
100
20 [dB]
0º
19 dB
A(ω) para KR=1.76
ψ(ω)
-90º
10 [dB]
19 dB
-45º
-180º
0 [dB]
γ=-161º
-10 [dB]
-270º
-206º
-20 [dB]
0.1
0.2
1
2 ωγ=3.6
10
20
[rad/s]
-360º
100
Bode de R(s)·G(s)·H(s)·e-s
El margen de fase con el retardo de un segundo en la realimentación sería γ=-161º, el sistema M(s) será inestable. Para
recuperar la estabilidad con un margen de fase de nuevo de γ=45º, habría que hacer “descender” la curva A(ω) 19 dB. Es decir,
multiplicar la KR actual por 10-19/20=0.1122: KR=1.76·0.1122 ≈0.2
APENDICE
Si el retardo fuese sólo de 0.1 segundos:
Hará que el margen de fase se reduzca haciendo al sistema en bucle cerrado menos estable. Esto se puede ver al trazar el
diagrama de bode de un retardo T=0.1 segundos que, al sumarlo al Bode anterior, dará como resultado que el margen de fase se
reducirá aproximadamente 20º.
G( s) =
Y(s)
= e −T · s
X(s)
20 [dB]
donde T = 0.1
-0º
20º
ψ(ω)
G ( jω ) = e −0.1·ω · j = 1 − 0.1·ω
10 [dB]
A(ω ) = 0 [ dB]
ψ (ω ) = −0.1·ω [rad ]
-45º
180
para ω γ = 3.6 ⇒ ψ (ω γ ) = −0.1·3.6·
= −20.6º 0 [dB]
π
A(ω)
-90º
Y(s)
X(s)
+
_
R(s)
H(s)·e-T·s
M(s)
G(s)
-135º
-10 [dB]
-180º
-20 [dB]
0.1
0.2
1
2
Para mantener el margen de estabilidad anterior sería necesario disminuir el valor de KR.
ωγ=3.6
10
20
[rad/s]
100