Ángulo agudo
Anuncio
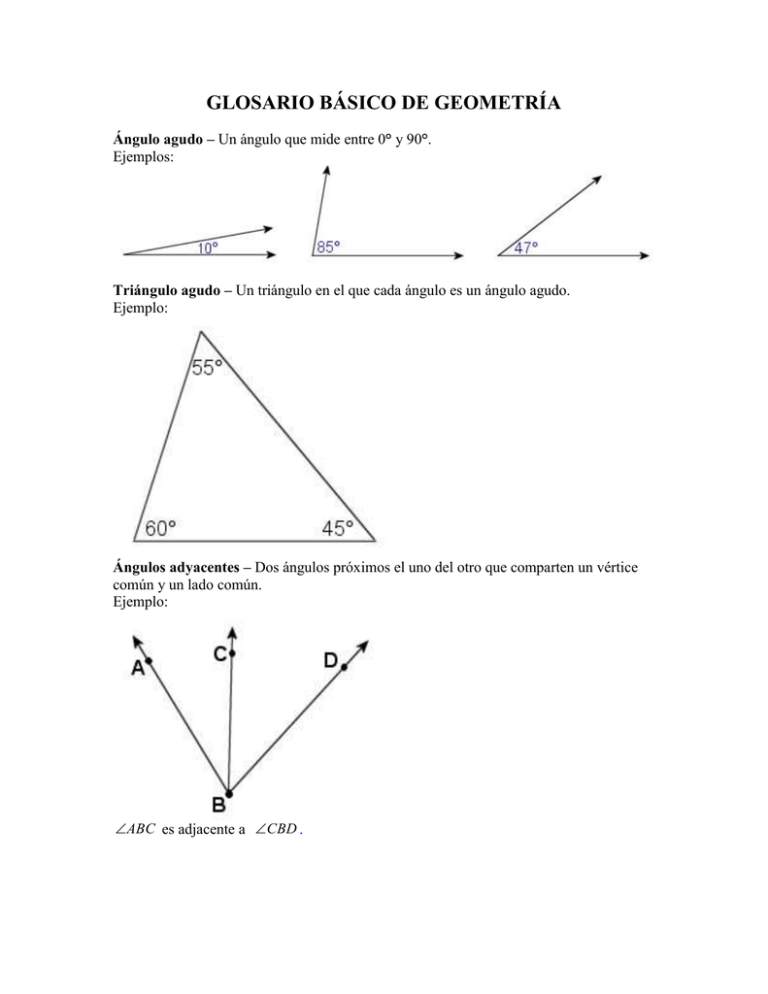
GLOSARIO BÁSICO DE GEOMETRÍA Ángulo agudo – Un ángulo que mide entre 0° y 90°. Ejemplos: Triángulo agudo – Un triángulo en el que cada ángulo es un ángulo agudo. Ejemplo: Ángulos adyacentes – Dos ángulos próximos el uno del otro que comparten un vértice común y un lado común. Ejemplo: ABC es adjacente a CBD . Ángulos alternos externos – Un par de ángulos que están en el exterior de las líneas y en lados opuestos de la transversal. Ejemplo: 1 y 8 y 2 y 7 son ángulos alternos externos. Ángulos alternos internos - Un par de ángulos que están en el interior de las líneas y en lados opuestos de la transversal. Ejemplo: 3 y 6 y 4 y 5 son ángulos alternos internos. Altura – (1) Altura. (2) El segmento perpendicular del vértice de un triángulo a la línea que contiene el lado opuesto. Ejemplo: Ángulo – Dos rayos que tienen un punto extremo común. Ejemplos: Bisectriz de un ángulo – Un rayo que divide un ángulo en dos ángulos adyacentes iguales. Ejemplo: Ángulo de depresión – El ángulo formado por la línea horizontal y la línea visual a un objeto por debajo de la horizontal. Ejemplo: Ángulo de elevación – El ángulo formado por la línea horizontal y la línea visual a un objeto por encima de la horizontal. Ejemplo: Horizontal Ángulo de incidencia – El ángulo formado por un rayo incidente en una superficie y una perpendicular a la superficie en el punto de incidencia. El ángulo de incidencia = el ángulo de reflexión. Ejemplo: Donde i es el ángulo de incidencia y r es el ángulo de reflexión. Ángulo de reflexión – El ángulo formado por un rayo reflejado y una perpendicular a la superficie en el punto de reflexión. El ángulo de reflexión = el ángulo de incidencia. Ejemplo: Donde i es el ángulo de incidencia y r es el ángulo de reflexión. Área – La cantidad de unidades cuadradas que cubre una superficie dada. ALA – (1) Suponga que tenemos dos triángulos ABC y DEF. Si un lado de ABC y dos ángulos que tienen este lado de ABC como uno de sus lados son iguales al lado correspondiente y a los dos ángulos del triángulo DEF, entonces los triángulos ABC y DEF son iguales. Ejemplo: La comprobación de lo anterior es: Dados: AC CD , B D . Compruebe: ABC EDC Comprobación: Afirmación Razón AC CD Dados B D Dados ACB ECD Ángulos verticales ABC EDC ALA (Ángulo-Lado-Ángulo) (2) Si dos ángulos de un triángulo son congruentes a los dos ángulos de otro triángulo, entonces los triángulos son semejantes. Se conoce como semejanza AA. Ejemplo: Base – La cara o el lado más bajo de una figura geométrica. Ángulo base de un triángulo isósceles – El ángulo que está opuesto a uno de los lados equiláteros de un triángulo isósceles. Hay dos ángulos base en un triángulo isósceles (vea el diagrama). Ejemplo: Ángulo base Base Ángulo base Puntos entremedios – En la figura, el punto B está entre A y C mientras que el punto Y no está entre A y B. Para que B esté entre A y C, todos los tres puntos deben ser colineales y B debe hallarse en el segmento AC. Centro geométrico – Donde las tres medianas de un triángulo se intersectan. También llamado centro de gravedad. Ejemplo: Círculo – Conjunto de todos los puntos en un plano que están a la misma distancia de un punto dado. Ejemplo: Circuncentro – La intersección de los tres bisectores perpendiculares de un triángulo. Ejemplo: Circunferencia – La distancia alrededor de un círculo. La formula de la circunferencia es: c 2 r o c d , donde r = radio y d = diámetro. Ejemplo: Circunscrito – Un polígono está circunscrito alrededor de un círculo si todos los lados del polígono son tangentes al círculo. Ejemplo: Colineal – En la misma línea. Ejemplo: Los puntos A, B, C, D y E son colineales mientras que F no lo es. Ángulos complementarios – Dos ángulos cuya medida suma 90°. Ejemplo: Donde EBD y DBC son ángulos complementarios. Polígono cóncavo – Un polígono que tiene por lo menos un ángulo interior mayor de 180° y tiene algunos de sus lados doblados hacia dentro. Ejemplos: Círculos concéntricos – Círculos que tienen diferentes radios pero comparten el mismo centro. Ejemplo: Cono – Una figura sólida que tiene un círculo por base y se estrecha gradualmente hasta terminar en una punta. Ejemplo: Congruente – Que tienen el mismo tamaño y la misma forma. Ejemplo: Donde ABC es congruente a DEF . Ángulos congruentes – Dos ángulos que tienen la misma medida. Escrito como A B. Ejemplo: Polígonos congruentes – Dos polígonos que tienen la misma forma y tamaño. Escrito como A B. Ejemplo: Segmentos congruentes – Dos segmentos que tienen la misma longitud. Escrito como A B. Ejemplo: Recíproco – Una condición inversa. Por ejemplo: si a b, entonces su recíproco es b a. Recíproco del teorema de Pitágoras – Esto afirma que la suma de los cuadrados de los lados más cortos de un triángulo es igual al cuadrado del lado más largo del triángulo, por lo tanto el triángulo es un triángulo recto. Esto se escribe como: c2 = a2 + b2. Polígono convexo – Un polígono en el que cada ángulo interior es menor o igual a 180°. Ejemplos: Coplanar – En el mismo plano. Ángulos correspondientes – Dos ángulos no adyacentes en el mismo lado de la transversal, con un ángulo interno y un ángulo externo a las líneas. Ejemplo: Donde 2 y 6 son ángulos correspondientes. Coseno – La razón de la longitud del lado que es adyacente al ángulo de la longitud de la hipotenusa en un triángulo rectángulo. Ejemplo: AB , donde AB es la longitud de los lados adyacentes y BC es la BC longitud de la hipotenusa. cosB (coseno de B ) = CPCTC – Cuando usted tiene dos triángulos congruentes, entonces todos los seis pares de las partes correspondientes (lados y ángulos) son congruentes. Esta afirmación es comúnmente conocida como las partes correspondientes de triángulos congruentes son congruentes, o por la abreviación (en inglés) CPCTC. Ejemplo: Para lo anterior, si ABC XYZ entonces AB ZY , BC YX , AC XZ , A Z , B Y y C X . Cubo – Un prisma cuadrado que tiene seis lados cuadrados iguales. Ejemplos: Cilindro – Una figura sólida con dos bases circulares y los lados rectos. Ejemplo: Diagonal – Un segmento de línea que une dos vértices no adyacentes de un polígono. Ejemplo: Diámetro – La distancia al cruzar un círculo a través de su centro. Ejemplo: El diámetro es AB. Dilatación – El proceso de agrandar o reducir una figura. Ejemplo: Distancia – La distancia entre dos puntos A y B se escribe como AB. Dodecaedro – Una figura sólida con 12 caras pentagonales regulares. Ejemplos: Triángulo equilátero – Un triángulo con todos los tres lados congruentes. Ejemplo: Triángulo equiangular – Un triángulo que tiene ángulos de la misma medida. Example: Ángulos externos – Los ángulos que están en la parte de afuera de dos líneas cortadas por una transversal. Ejemplo: Donde 1 , 2 , 7 y 8 son ángulos externos. Heptágono – Un polígono de siete caras. La suma de sus ángulos es de 900°. Ejemplo: Hexágono – Un polígono de seis lados. La suma de sus ángulos es de 720°. Ejemplo: Prisma hexagonal – Un prisma compuesto de dos caras hexagonales y seis paralelogramos. Ejemplo: Hipotenusa de un triángulo rectángulo – El lado de un triángulo rectángulo que es opuesto al ángulo recto. Ejemplo: Icosaedro – Una figura sólida de 20 caras las cuales son triángulos equiláteros. Ejemplos: Incentro – La intersección de los bisectrices de los tres ángulos en el triángulo ABC. Ejemplo: Ángulo incluido – El ángulo formado por dos lados de un polígono. Ejemplo: Donde A es un ángulo incluido formado por los lados a y d, B es un ángulo incluido formado por los lados a y b, C es un ángulo incluido formado por los lados b y c, y D es un ángulo incluido formado por los lados c y d. Lado incluido – El lado que está entre dos ángulos en un polígono. Donde a es un lado incluido formado por A y B, b es un lado incluido formado por B y C, c es un lado incluido formado por C y D, y d es un lado incluido formado por D y A. Inscrito – Un polígono está inscrito en un círculo si todos sus vértices están en el círculo. Ejemplo: Ángulos internos – Ángulos que están en la parte interior de dos líneas cortadas por una transversal. Ejemplo: Donde 3 , 4 , 5 y 6 son ángulos internos. Líneas que se intersectan – Dos líneas que se cruzan en un sólo punto. Ejemplo: 1 Recíproco inverso – Lo opuesto del recíproco de x es . x 1 Ejemplos: 2 es el inverso recíproco de 2 1 es el inverso recíproco de 2 2 Trapecio isósceles – Un cuadrilátero con un par de lados paralelos con al menos dos lados de la misma longitud. Ejemplo: Triángulo isósceles – Un triángulo con al menos dos lados congruentes. Ejemplo: Cometa – Un cuadrilátero que tiene dos pares distintos de lados equiláteros consecutivos. Ejemplo: Catetos de un triángulo rectángulo – Cualquiera de los dos lados que forman un ángulo recto de un triángulo rectángulo. Ejemplo: Cateto Cateto Catetos de un triángulo isósceles – Uno de los dos lados congruentes en un triángulo isósceles. Ejemplo: Línea – Un conjunto de puntos que están perfectamente derechos y se extienden sin fin. Puede ser nombrada por una letra minúscula o por dos puntos en la línea. Si es nombrada por dos puntos en la línea, se usa una flecha de doble punta sobre las dos letras, ej. AB . Ejemplo: Se escribe como la línea XY o XY . Par lineal – Dos ángulos adyacentes suplementarios que forman una línea con sus lados no comunes. Ejemplo: Línea de simetría – Una línea que separa a una figura en dos partes congruentes o iguales. Ejemplos: Las rayas intermitentes son la líneas de simetría. Mediana – (1) La mediana de un trapecio es paralela a las bases, y su medida es la mitad de la suma de las medidas de las bases. La mediana de un trapecio es el segmento que une los puntos medios de sus catetos, como se muestra abajo. (2) El segmento del vértice de un triángulo al punto medio del lado opuesto. Ejemplo: Mediana Mediana = 5 15 2 = 7.5 Punto medio – El punto que divide una línea en dos partes iguales. Ejemplo: Donde M es el punto medio de AB . No-colineal – Cuando puntos no están en la misma línea. Ejemplo: Donde los puntos A, B y D son no colineales. No coplanario – Cuando lineas no están en el mismo plano. Ángulo obtuso – Un ángulo que tiene una medida mayor de 90° pero menor de 180°. Ejemplo: Triángulo obtuso – Un triángulo que tiene un ángulo obtuso. Ejemplo: Octágono – Un polígino de ocho lados. La suma de sus ángulos es de 1080°. Ejemplo: Octaedro – Una figura sólida de ocho caras constituidas por triángulos equiláteros. Ejemplos: Ortocentro – El punto de intersección de las tres altitudes de un triángulo. Ejemplo: Líneas paralelas – Líneas que no intersectan en un mismo plano. Ejemplo: Escrito como AB XY . Paralelogramo – Un cuadrilátero con dos pares de lados opuestos paralelos. Ejemplo: Pentágono – Un polígono de cinco lados. La suma de sus ángulos es de 540°. Ejemplo: Perímetro – La distancia alrededor de una figura. Ejemplo: El perímetro de esta figura es: 2cm + 2cm + 3cm = 7cm. Bisectriz perpendicular – Una línea, o segmento de línea, que intersecta o cruza a un segmento de línea dado en su punto medio y forma ángulos rectos. Ejemplo: La línea XY es el bisector perpendicular del segmento AB. Escrito como XY es el bisector perpendicular de AB . Líneas perpendiculares – Líneas que se cruzan para formar ángulos rectos. Ejemplo: La línea XY es perpendicular a la línea AB. Escrito como XY AB . Plano – Un conjunto de puntos que forman una superficie plana que se extiende en todas direcciones sin fin. Ejemplo: Pi – Escrito ; es la razón de la circunferencia al diámetro de un círculo. Circunferencia/Diámetro. También redondeado a 3. 14. Punto – Generalmente representado por una señal, pero sin tamaño. Use letras mayúsculas para nombrarlos. Poliedro – Figura sólida tridimensional que consiste de polígonos, generalmente unidos por los lados. Polígono – Figura plana cerrada que resulta al unir tres o más segmentos de línea en sus puntos extremos. Ejemplos: Prisma – Figura sólida que tiene dos bases que son paralelas, polígonos congruentes y con todas las otras caras que son paralelogramos. Ejemplos: Pirámide – Figura sólida con un polígono de base y con todas las otras caras triangulares que comparten un vértice común. Ejemplos: Teorema de Pitágoras – En un triángulo rectángulo a2 + b2 = c2, donde a y b son las longitudes de los catetos del triángulo y c es la longitud de la hipotenusa del triángulo. Triple de Pitágoras – Un grupo de tres números enteros que pueden ser la longitud de los lados de un triángulo rectángulo. Ejemplo: 3, 4 y 5, donde c es el número más grande. Cuadrilátero – Un polígono con cuatro lados. La suma de los ángulos es de 360°. Ejemplos: Radio – Un segmento de línea que se dibula desde un punto en el círculo al centro del círculo. Ejemplo: El radio es AB. Rayo – Un segmento de línea que comienza en un punto extremo y se extiende sin fin en una sóla dirección. Ejemplo: Rayo AB, escrito como AB . Recíproco de un número – Uno de dos números cuyo producto es 1. El recíproco de x es 1 . x 1 Ejemplos: 2 es el recíproco de 2 1 es el recíproco de 2 2 Rectángulo – Un cuadrilátero con cuatro ángulos rectos. La suma de sus ángulos es de 360°. Ejemplos: Prisma rectangular – (1) Una figura sólida con dos bases que son rectángulos y con todas las otras caras que son paralelogramos. (2) Un prisma en la forma de un rectángulo. Ejemplos: Reflejo – Una imagen de espejo que se dibuja de una figura sobre su línea de simetría. Ejemplo: Polígono regular – Un polígono que tiene todos los lados iguales y todos los ángulos iguales. Ejemplos: Rombo – Un polígono que tiene todos los lados congruentes. La suma de sus ángulos es de 360°. Ejemplos: Ángulo recto – Un ángulo cuya medida es de 90°. Ejemplo: Prisma recto – Un prisma que tiene dos características especiales: todos las aristas laterales son perpendiculares a las bases y todas las caras laterales son rectangulares. Ejemplo: Triángulo rectángulo – Un triángulo que tiene un ángulo recto. Ejemplo: Rotación – El movimiento de una figura geométrica alrededor de un eje fijo. Ángulos internos del mismo lado – Ángulos internos en el mismo lado de una transversal. Ejemplo: Donde 3 y 5 , 4 y 6 son ángulos internos del mismo lado. LAL – (1) Supongamos que tenemos dos triángulos ABC y DEF. Si dos lados y un ángulo de ABC son iguales a dos lados y un ángulo de DEF, entonces el triángulo ABC es igual al triángulo DEF. Ejemplo: La verificación o prueba de lo dicho anteriormente es: Dados: AC CD , BC CE . Compruebe: ABC EDC Comprobación: Afirmación Razón AC CD Dados BC CE Dados ACB ECD Ángulos verticales ABC EDC LAL (Lado-Ángulo-Lado) (2) Si las medidas de dos lados de un triángulo son proporcionales a las medidas de los dos lados correspondientes de otro triángulo y los ángulos incluidos son congruentes, entonces los triángulos son semejantes. Ejemplo: 4 5 8 10 Triángulo escaleno – Un triángulo con lados que no son congruentes. Ejemplos: Segmento – El segmento de línea AB forma parte de la línea x entre los puntos A y B incluyendo estos puntos. Ejemplo: Segmento bisectriz – Cualquier línea, segmento o rayo que intersecta a un segmento en su punto medio. Ejemplo: La línea X es un segmento bisectriz. Polígonos semejantes – Polígonos que tienen la misma forma, pero no necesariamente el mismo tamaño. Ejemplo: Seno – La razón de la longitud del lado opuesto a un ángulo a la longitud de la hipotenusa en un triángulo rectángulo. Ejemplo: senB (seno de B ) = AC , donde AC es la longitud del lado opuesto y BC es la longitud BC de la hipotenusa. Líneas oblicuas - Las líneas son oblicuas si no están en el mismo plano. Pendiente de una línea – La inclinación de una línea. Esfera – Una figura sólida en que todos los puntos de la superficie están a la misma distancia del centro. Ejemplo: Cuadrado – Un cuadrilátero con cuatro ángulos rectos y cuatro lados congruentes. La suma de sus ángulos es de 360°. Ejemplo: Prisma cuadrado – Una figura sólida siendo las bases cuadradas y todas las otras caras paralelogramos. Ejemplo: LLL (Lado-Lado-Lado)– (1) Si los tres lados del triángulo ABC son iguales a los tres lados del triángulo DEF, entonces los triángulos ABC y DEF son iguales. Ejemplo: La comprobación de lo anterior es: Dados: AC CD , AB BD . Compruebe: Comprobación: Afirmación Razón AC CD Dados AB BD Dados ABC DBC BC CB ABC DBC Lado común LLL (Lado-Lado-Lado) (2) Si las medidas de los lados correspondientes de dos triángulos son proporcionales, entonces los triángulos son semejantes. Ejemplo: 4 6 8 2 3 4 Suplementarios – Se dice que dos ángulos son suplementarios si la suma de sus medidas es de 180°. Ejemplo: Ángulos suplementarios – La suma de dos ángulos cuya medida es igual a 180°. Ejemplo: m ACD + m DCB = 78° + 102° = 180° Área de superficie – La suma de todas las areas de las superficies de una figura sólida. Tangente – (1) La razón de la longitud del lado opuesto a un ángulo a la longitud del lado adyacente al ángulo en un triángulo rectángulo. Ejemplo: AC , donde AC es la longitud del lado opuesto y AB es la AB longitud del lado adyacente. (2) Una línea es tangente a un círculo si intersecta al círculo en exactamente un punto. Ejemplo: tanB (tangente de B) = AB es tangente al círculo en el punto C. Tetraedro – Una figura sólida con cuatro caras que son triángulos equiláteros. Ejemplo: Transformación – El cambio en tamaño, forma, o posición de una figura geométrica. Traslación – Cuando se mueve una figura geométrica a una nueva posición sin darle la vuelta o sin volverla a si misma. Transversal – Una línea que intersecta a dos o más líneas. Ejemplo: Trapecio – Un cuadrilátero con exactamente un par de lados opuestos paralelos. La suma de sus ángulos es de 360°. Ejemplos: Trigonometría – Las matemáticas que se ocupan de las medidas triangulares. Triángulo – Un polígino de tres lados. La suma de sus ángulos es de 180°. Ejemplos: Prisma triangular – Un prisma compuesto de dos caras triangulares y tres paralelogramos. Ejemplo: Vértice – El punto extremo común de dos rayos que forman un ángulo. Ejemplos: Vértice del ángulo de un triángulo isósceles – El ángulo que se forma en un triángulo isósceles donde se encuentran los dos lados congruentes (catetos). También conocido como el ángulo opuesto a la base de un triángulo isósceles. Ejemplo: Ángulos verticales – Ángulos de la misma medida que se forman cuando dos líneas se intersectan. Ejemplo: ACB y DCE son ángulos verticales. Vértices – Los puntos en una figura donde se intersectan las líneas. Volumen – el número de unidades cúbicas que se necesitan para ocupar un espacio dado.