Raí - ies inca garcilaso

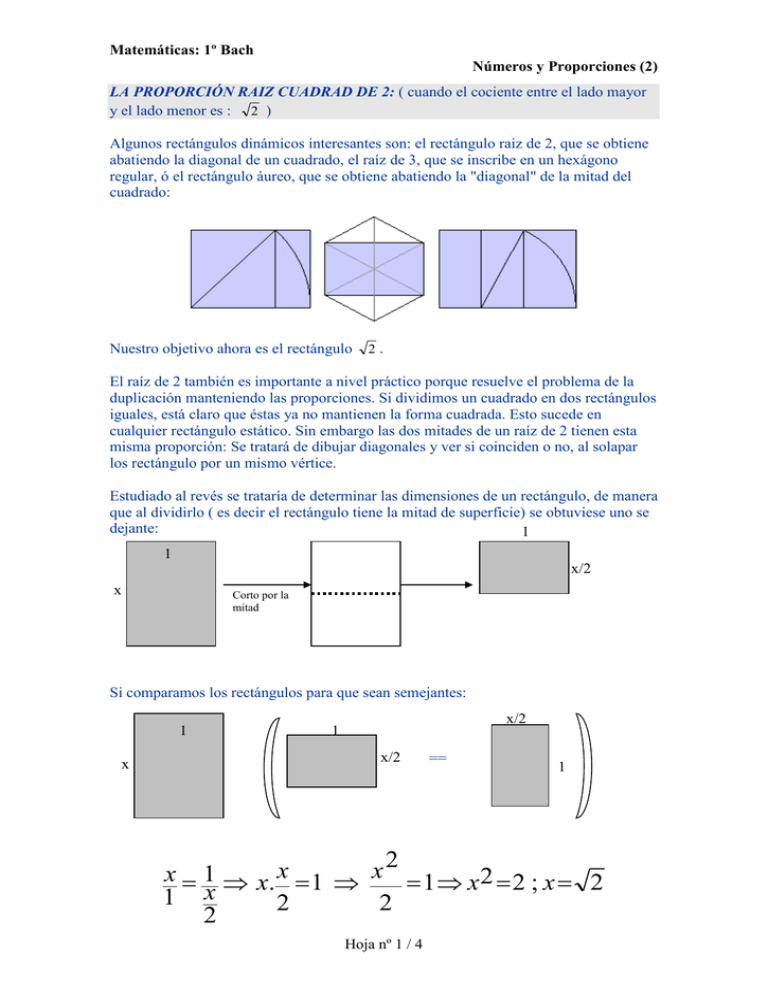
Matemáticas: 1º Bach
Números y Proporciones (2)
LA PROPORCIÓN RAIZ CUADRAD DE 2: ( cuando el cociente entre el lado mayor
y el lado menor es : 2 )
Algunos rectángulos dinámicos interesantes son: el rectángulo raiz de 2, que se obtiene
abatiendo la diagonal de un cuadrado, el raíz de 3, que se inscribe en un hexágono
regular, ó el rectángulo áureo, que se obtiene abatiendo la "diagonal" de la mitad del
cuadrado:
Nuestro objetivo ahora es el rectángulo
2.
El raíz de 2 también es importante a nivel práctico porque resuelve el problema de la
duplicación manteniendo las proporciones. Si dividimos un cuadrado en dos rectángulos
iguales, está claro que éstas ya no mantienen la forma cuadrada. Esto sucede en
cualquier rectángulo estático. Sin embargo las dos mitades de un raíz de 2 tienen esta
misma proporción: Se tratará de dibujar diagonales y ver si coinciden o no, al solapar
los rectángulo por un mismo vértice.
Estudiado al revés se trataría de determinar las dimensiones de un rectángulo, de manera
que al dividirlo ( es decir el rectángulo tiene la mitad de superficie) se obtuviese uno se
dejante:
1
1
x/2
x
Corto por la
mitad
Si comparamos los rectángulos para que sean semejantes:
1
x
x/2
1
x/2
==
1
2
x  1  x. x  1  x  1  x 2  2 ; x  2
1 x
2
2
2
Hoja nº 1 / 4
Matemáticas: 1º Bach
Números y Proporciones (2)
Que hace que nuestro rectángulo original tenga las dimensiones:
1
2
Y en general sería de
dimensiones: ……….
a
a 2
Al revés también podríamos haber razonado; Partimos de un rectángulo, hacemos uno
que sea el doble de grande y queremos que sea semejante. Volveríamos a obtener como
dimensiones: a y a 2
… Y siempre muy fácil de reconocer comprobando si el lado mayor es la diagonal del
cuadrado que se forma con el lado menor:
… Lo interesante de esta proporción es lo que la utilizamos todos los días en nuestro
trabajo tomando apuntes, haciendo ejercicios, etc.
La serie DIN-A ha normalizado los formatos de papel a partir de un rectángulo de un
metro cuadrado de superficie con sus lados en proporción 1 a raíz de 2, que es el
formato A-0. Su mitad es el formato A-1, la mitad de éste es el A-2, la mitad de éste A3, y así con el A-4 que sustituye los tradicionales formatos arbitrarios de folio, el A-5
que sustituye la cuartilla, el A-6 la octavilla, etc. etc.
Hoja nº 2 / 4
Matemáticas: 1º Bach
Números y Proporciones (2)
¿Por qué tiene nuestra hoja de papel, con esta interesante propiedad de repetir su forma
de manera semejante al dividirla por la mitad o al duplicarla, unas dimensiones tan
rarísimas: 210 mm x 297 mm ?.
Este es el EJERCICIO DE LA ACTIVIDAD, para ello comencemos con nuestro
modelo A4, supongamos que sus dimensiones son:
x 2
x
Y vayamos reconstruyendo los diferentes formatos hasta llegar al A0, sabiendo de este
que tiene una superficie de 1 m2= 1000000 mm2
…. Pero si dejamos la mesa de trabajo y nos adentramos en el mundo de la producción
artística fotográfica, nos encontramos que en las cámaras de fotografía, en la parte
superior del objetivo, aparece la siguiente seria de números que se llaman “ f ”:
f:1’4 –f:2 – f:2’8 – f:4 – f:5’6 –f:8 – f:11 – f:16 – f:22 ‘6 – f:32.
¿Que tienen que ver con la siguiente tabla de números ( que empieza con raíz de 2 )?.. ¿
a qué números corresponde?:
1,41421356
2
2,82842712
4
5,65685425
8
11,3137085
16
22,627417
32
… ¿ Y por qué otra vez una serie con
números?
0,70710678
0,5
0,35355339
0,25
0,1767767
0,125
0,08838835
0,0625
0,04419417
0,03125
2 ? ( No deberían de ser los inversos de estos
Hoja nº 3 / 4
Matemáticas: 1º Bach
Números y Proporciones (2)
La razón como ocurría con las hojas DIN, es que en cada cambio de diafragma,se
obtiene una superficie que es la mitad ( si lo cerramos) o el doble ( si lo abrimos)
Relación entre variación del lado
y variación de la superficie:
Si tenemos un diafragma abierto ( un círculo de radio “ r “ ) y cerramos una vez el
diafragma se obtiene un círculo cuya superficie es la mitad de la anterior y el radio
disminuye dividiendo por la Raiz de 2, el radio anterior
r
2
r
( 2)
r
2
( 2 )3
… si te fijas bien sólo se ponen los números de los denominadores.
Para terminar 2 es un número asociado a la construcción del cuadrado. Existe una
parte algo esotérica de las matemáticas, que se llama geometría sagrada, en la que
puedes encontrar originales y sugerentes interpretaciones de lo que representa el
cuadrado y este número irracional en la construcción e interpretación de nuestro mundo
y de nuestra vida y espiritualidad. Pero esto es otra historia.
Hoja nº 4 / 4