diseño de clase
Anuncio
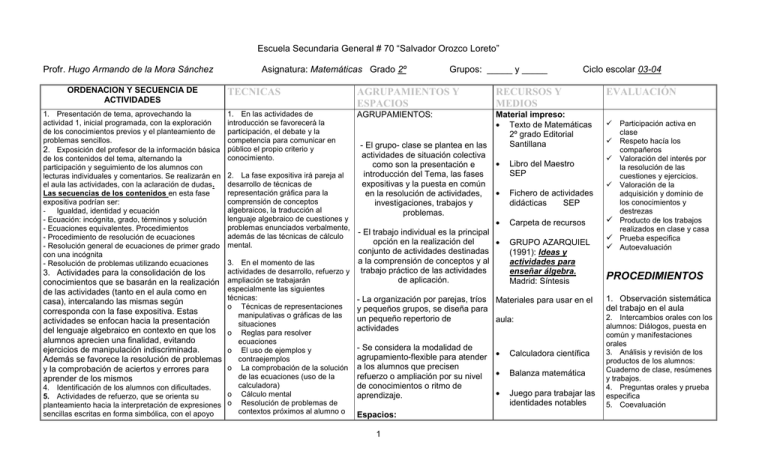
Escuela Secundaria General # 70 “Salvador Orozco Loreto”
Profr. Hugo Armando de la Mora Sánchez
ORDENACION Y SECUENCIA DE
ACTIVIDADES
1. Presentación de tema, aprovechando la
actividad 1, inicial programada, con la exploración
de los conocimientos previos y el planteamiento de
problemas sencillos.
2. Exposición del profesor de la información básica
de los contenidos del tema, alternando la
participación y seguimiento de los alumnos con
lecturas individuales y comentarios. Se realizarán en
el aula las actividades, con la aclaración de dudas.
Las secuencias de los contenidos en esta fase
expositiva podrían ser:
- Igualdad, identidad y ecuación
- Ecuación: incógnita, grado, términos y solución
- Ecuaciones equivalentes. Procedimientos
- Procedimiento de resolución de ecuaciones
- Resolución general de ecuaciones de primer grado
con una incógnita
- Resolución de problemas utilizando ecuaciones
Asignatura: Matemáticas Grado 2º
Grupos: _____ y _____
Ciclo escolar 03-04
TECNICAS
AGRUPAMIENTOS Y
ESPACIOS
RECURSOS Y
MEDIOS
1. En las actividades de
introducción se favorecerá la
participación, el debate y la
competencia para comunicar en
público el propio criterio y
conocimiento.
AGRUPAMIENTOS:
Material impreso:
Texto de Matemáticas
2º grado Editorial
Santillana
2. La fase expositiva irá pareja al
desarrollo de técnicas de
representación gráfica para la
comprensión de conceptos
algebraicos, la traducción al
lenguaje algebraico de cuestiones y
problemas enunciados verbalmente,
además de las técnicas de cálculo
mental.
- El grupo- clase se plantea en las
actividades de situación colectiva
como son la presentación e
introducción del Tema, las fases
expositivas y la puesta en común
en la resolución de actividades,
investigaciones, trabajos y
problemas.
Libro del Maestro
SEP
Fichero de actividades
didácticas
SEP
Carpeta de recursos
- El trabajo individual es la principal
opción en la realización del
GRUPO AZARQUIEL
conjunto de actividades destinadas
(1991): Ideas y
a
la
comprensión
de
conceptos
y
al
actividades para
3. En el momento de las
trabajo
práctico
de
las
actividades
actividades de desarrollo, refuerzo y
enseñar álgebra.
3. Actividades para la consolidación de los
de aplicación.
Madrid: Síntesis
conocimientos que se basarán en la realización ampliación se trabajarán
especialmente las siguientes
de las actividades (tanto en el aula como en
técnicas:
- La organización por parejas, tríos Materiales para usar en el
casa), intercalando las mismas según
o Técnicas de representaciones
y pequeños grupos, se diseña para
corresponda con la fase expositiva. Estas
manipulativas o gráficas de las
un pequeño repertorio de
aula:
actividades se enfocan hacia la presentación
situaciones
actividades
del lenguaje algebraico en contexto en que los o Reglas para resolver
alumnos aprecien una finalidad, evitando
ecuaciones
- Se considera la modalidad de
ejercicios de manipulación indiscriminada.
o El uso de ejemplos y
agrupamiento-flexible para atender Calculadora científica
contraejemplos
Además se favorece la resolución de problemas
o La comprobación de la solución a los alumnos que precisen
y la comprobación de aciertos y errores para
Balanza matemática
de las ecuaciones (uso de la
refuerzo o ampliación por su nivel
aprender de los mismos
calculadora)
de conocimientos o ritmo de
4. Identificación de los alumnos con dificultades.
Juego para trabajar las
o
Cálculo
mental
aprendizaje.
5. Actividades de refuerzo, que se orienta su
o
Resolución
de
problemas
de
identidades notables
planteamiento hacia la interpretación de expresiones
contextos próximos al alumno o
sencillas escritas en forma simbólica, con el apoyo
Espacios:
1
EVALUACIÓN
Participación activa en
clase
Respeto hacía los
compañeros
Valoración del interés por
la resolución de las
cuestiones y ejercicios.
Valoración de la
adquisición y dominio de
los conocimientos y
destrezas
Producto de los trabajos
realizados en clase y casa
Prueba especifica
Autoevaluación
PROCEDIMIENTOS
1. Observación sistemática
del trabajo en el aula
2. Intercambios orales con los
alumnos: Diálogos, puesta en
común y manifestaciones
orales
3. Análisis y revisión de los
productos de los alumnos:
Cuaderno de clase, resúmenes
y trabajos.
4. Preguntas orales y prueba
especifica
5. Coevaluación
de actividades manipulativas, gráficas y problemas
“tipo resueltos, además del aprovechamiento del
tiempo encasa y el uso del programa FORACIT “El
integrador matemático” en el aula de medios
Actividades de ampliación: Que desarrollan la
aplicación de las cuestiones algebraicas y de las
ecuaciones a situaciones problemáticas concretas
del contexto y la utilización de gráficos.
sobre los que tenga la posibilidad
de conocimiento, en los que se
use la estrategia: distintos
planteamientos mediante
ecuaciones.
o Uso de aplicaciones
informáticas
-
Aula ordinaria
Aula de medios
Aula de
audiovisuales (si la
hay)
Cuaderno de ejercicios
Material para CP
2
Programa Foracit
Hoja electrónica de
cálculo
EMAT (Calculadora
virtual)
Instrumentos:
-Ficha personal de registro
(actitudes, participación
interés y respeto)
-Prueba escrita con ejercicios
de aplicación.
-Ejercicios que incluyen las
respuestas (autoevaluación)
Escuela Secundaria General # 70 “Salvador Orozco Loreto”
Profr. Hugo Armando de la Mora Sánchez
Plan de clase:
Asignatura: Matemáticas Grado 2º
Tema 2 “Ecuaciones lineales con una incógnita
Grupos: _____ y _____
Ciclo escolar 03-04
No. de sesiones 6
Propósitos de la unidad: al termino de la unidad, el alumno:
Sabrá analizar problemas que conducen a ecuaciones lineales. Identificará la ecuación lineal y la relación entre ecuaciones y funciones de primer grado. Solucionará ecuaciones por métodos algebraicos. Estará
familiarizado con las operaciones a realizar en ambos lados de la igualdad, transponiendo términos de un lado a otro.
CONTENIDOS
PREVIOS
Operaciones con números
enteros (+ -)
CONCEPTUALES
Leyes de los signos
Uso del paréntesis
Operaciones con monomios y
binomios (suma, resta y
multiplicación)
Jerarquía de las operaciones
Lenguaje algebraico
PROCEDIMENTALES
1) El desarrollo del contenido se iniciará con problemas
sencillos, y que gradualmente se manejen otros de
mayor complejidad, insistiendo que es fundamental
Propiedades de la igualdad
poder expresar con facilidad los números y sus
relaciones, para poder manejar de manera más
Utilización del método de la balanza
adecuada y sencilla los problemas de mayor
generalidad.
Ecuaciones: incógnita, grado, términos y solución
2) Los alumnos empezarán realizando conversiones del
lenguaje cotidiano al lenguaje algebraico, para
Ecuaciones equivalentes
posteriormente insistir en las operaciones que se
involucran, y después concluir con el manejo de
Procedimientos de resolución de ecuaciones
ecuaciones de primer grado con una incógnita y su
solución.
Resolución general de la ecuación de primer grado
3)
Con la finalidad de superar las dificultades de los
con una incógnita
alumnos por traducir las expresiones cotidianas,
fomentar el uso y significado de los paréntesis para
Resolución de problemas que den lugar a una
efectuar las operaciones de manera correcta; se
ecuación de primer grado con una incógnita,
proponen tres actividades para que al terminar de
utilizando los cinco pasos:
realizar cada una, el profesor aclare el porqué de los
errores que seguramente manifestarán los alumnos.
1. Analizar el enunciado
Esto se considerará como un examen de diagnóstico.
2. Expresarlo en lenguaje simbólico
1. Se practicará la traducción al lenguaje
3. Resolver la ecuación correspondiente
algebraico. Se le indica a los alumnos expresiones
4. Verificar si el resultado obtenido satisface
en lenguaje cotidiano y en álgebra, para que las
las condiciones del problema
relacione, en las expresiones, se señalan las
5. Dar la respuesta
operaciones básicas. (VER ANEXO)
ACTITUDINALES
Igualdad identidad y ecuación
3
Valoración de la precisión,
simplicidad y utilidad del lenguaje
algebraico para representar,
comunicar y resolver situaciones de
la vida cotidiana.
Valoración y respeto por su
trabajo y el de sus compañeros
Gusto por la presentación y
orden de las soluciones de las
ecuaciones
UNIDAD 2: Tema Ecuaciones lineales con una incógnita
(anexo)
CONTENIDOS PROCEDIMENTALES
2. Se realizarán operaciones en donde se indican paréntesis y sus efectos en la representación de las
expresiones algebraicas
3.
Aclarar los diferentes elementos como coeficiente, exponente, número de variables y grado de una
expresión, dichos conceptos se analizarán por medio de una tabla.
Para iniciar el desarrollo del tema, se propone empezar con un problema sencillo, en el que la solución
prácticamente se obtenga sin ningún problema y gradualmente se introduzcan problemas de mayor
complejidad. A continuación, se presentan las actividades como una muestra de los ejemplos que se
pueden desarrollar:
ACTIVIDAD 1: Para resolver eficientemente un problema en matemáticas, es fundamental poder
expresar con facilidad los números con sus relaciones, y poder realizar las manipulaciones
correspondientes.
Lo primero que se debe hacer, para resolver un problema es traducir el problema del lenguaje cotidiano
al lenguaje algebraico, Realiza el siguiente ejercicios: relaciona las siguientes columnas (ver tabla
anexa 1)
Actividad 2: Evaluación de expresiones algebraicas
En una expresión algebraica las variables representan números.
El valor numérico de una expresión puede calcularse cuando a cada variable
de la expresión se le asigna un valor especifico.
Se llama evaluación al proceso de calcular el valor numérico de una
expresión
Por ejemplo: Evaluar la expresión 2a + 2b cuando: a = 5 y b = 7 solución:
2(5) + 2(7) = 10 + 14 = 24 respuesta: 24: Como ejercicio los alumnos
evaluarán 10 expresiones
Actividad 3: Determinación de variables y grado de las variables
Se considera conveniente antes de realizar operaciones con el fin de poder simplificar, y solucionar
ecuaciones, es necesario definir el grado de una variable, grado de un monomio y el de un polinomio.
Por lo que se propone el llenado y análisis de la siguiente tabla (ver tabla anexa
Actividad 4: Ejemplos desarrollados
4
Iniciaremos con un problema sencillo de fácil solución, haciéndoles a los alumnos la aclaración de que
de momento lo que más importa es el planteamiento.
Problema 1: Los organizadores de la fiesta del día del estudiante,
determinaron que los gastos serán de $1250.00 y en el grupo están dispuestos
a cooperar solo 35 alumnos, ¿Cuánto debe aportar cada uno de los alumnos?
a) ¿Cuál es la ecuación que representa el planteamiento del problema?
b) ¿Cuál es la variable que hay que determinar y que nos da la solución del
problema
c) ¿Cuál es el valor de la variable o incógnita?
d) ¿Cómo se obtuvo el valor de la variable?
e) ¿Es correcta la solución?
f) ¿Cómo se comprueba?
(Realizar ejercicios como el del ejemplo)
Actividad 5: Planteamiento de ecuaciones
Problema 1: La suma de tres números es 123. El segundo número es el doble del primero y el tercero
supera en tres al segundo. Determinar los tres números
1. ¿Cómo representas el primer número?
__________________
2. ¿Cómo representas el segundo número?
__________________
3. ¿Cómo representas el tercer número?
__________________
4. ¿Cómo representas que la suma de los tres números es 123? ___________________
5. Determina los números si la suma es 246
___________________
6. ¿Cuáles son los números si la suma es 63?
___________________
Problema 2: La anchura de un rectángulo es de x metros. ¿Cuál es el perímetro si su longitud (largo)
fuera el doble del ancho?
1) ¿Cómo representas: su anchura?
2) ¿Cómo representas: su longitud es el doble del ancho?
3) ¿Cómo representas: su perímetro?
4) ¿Cuál es su perímetro si su anchura es el triple del ancho?
(trabajar con más problemas como los del ejemplo)
Actividad 6: Ecuaciones con una sola variable ( de la forma ax = b)
Ecuación 1:
2x = 20
El coeficiente de x es 2
El inverso multiplicativo de 2 es ½
5
Multiplica ambos miembros de la igualdad por ½
2x(1/2) = 20 (1/2)
x = 10
haga la comprobación (realizar ejercicios del texto página 69)
Actividad 7: Resolver una ecuación de la forma ax + b = c
Ecuación 1:
3x + 3 = 42
resta 3 a ambos miembros de la ecuación. Propiedad uniforme de la
igualdad
3x + 3 – 3 = 42 – 3
3x = 39
el coeficiente de x es 3, el inverso multiplicativo de 3 es 1/3, se
multiplican ambos miembros de la ecuación por 3 x (1/3) = 39 (1/3)
1x = 13
Haz la comprobación
(trabajar con los ejercicios 1,2,3 y4 del texto, página 71)
Actividad 8: Solución de problemas
Plantear y resolver los siguientes problemas ( trabajar con el ejercicio 2 del texto, página 73)
6
UNIDAD 2: ECUACIONES LINEALES
PLAN DE UNIDAD DIDACTICA
Elaborado por el Profr. Hugo Armando de la Mora Sánchez para 2º y 3º grado
SENTIDO DE LA UNIDAD
En esta unidad se pretende dotar a los alumnos de los elementos algebraicos que les permitan generar, manipular y
solucionar las ecuaciones de primer grado con una incógnita, este tema será básico ya que será retomado en otras unidades.
Se pretende que el alumno recuerde y aplique los conocimientos adquiridos con anterioridad en el 1º de secundaria, pero
más que repetir, el alumno deberá profundizar y aclarar las dudas que se le presentan, al mismo tiempo que adquiere mayor
dominio en la manipulación y tratamiento de las ecuaciones.
Durante el desarrollo de esta unidad, el alumno deberá adquirir la habilidad de reconocer las variables que intervienen en
la solución de un problema, la expresión algebraica que refleja las relaciones entre los elementos que definen el problema
y la manipulación algebraica en el proceso de resolver o solucionar una ecuación.
Otros aspectos que se pretenden clarificar en esta unidad son los elementos del lenguaje algebraico en el manejo de la
solución algebraica de una ecuación y su comprobación; por ejemplo los términos semejantes y operaciones algébricas
Es decir, se pretende que en esta unidad se pueda conceptuar a la expresión algebraica como la generalización del
tratamiento de operaciones y métodos de solución de casos especiales.
PROPÓSITOS DE LA UNIDAD:
Al termino de la Unidad, el alumno:
a) Sabrá analizar problemas que conducen a ecuaciones lineales.
b) Identificará la ecuación lineal y la relación entre ecuaciones y funciones de primer grado.
c) Solucionará ecuaciones lineales por métodos algebraicos.
7
d) Estará familiarizado con las operaciones a realizar en ambos lados de la igualdad, trasponiendo términos de un lado a
otro.
CONTENIDOS.
Problemas introductorios; Su solución por inversión de operaciones y otros métodos, por ejemplo, por medio de una tabla de
valores, de una gráfica o de un modelo o diagrama geométrico.
Métodos algebraicos de solución:
operaciones con ambos miembros de una ecuación
trasposición de términos y solución de ecuaciones de la forma:
ax + b = c
ax + bx + c = d
ax + b = cx + d
etc.
y casos sencillos de ecuaciones con paréntesis.
Planteo y solución de problemas que conducen a ecuaciones lineales.
CONEXIONES CON OTROS TEMAS
La presente unidad es básica para el desarrollo de otros temas, tiene conexiones con las siguientes unidades de los
programas de Matemáticas III
Unidad 3 de Matemáticas de 3º grado, en donde se solucionarán Sistemas de Ecuaciones Lineales.
8
Unidad 4 de Matemáticas 3º grado, ya que en esta unidad se utilizarán los métodos de factorización y manejo de factores
lineales en la solución de Ecuaciones Cuadráticas y Factorización.
Unidad 3 de Matemáticas 3º grado, en vista de que en esta unidad se analizarán casos y soluciones de ecuaciones con
Expresiones Racionales y con Radicales que se pueden reducir a lineales.
Unidad 2 de Matemáticas 3º grado donde se manejan las Inecuaciones y Regiones en el Plano, por lo que se tratarán las
desigualdades lineales.
Unidad 1 de Matemáticas 2º grado, en la que se dará Solución Numérica a Sistemas de Ecuaciones lineales, con sus
correspondientes alternativas: una solución, ninguna solución y muchas soluciones.
Unidad 3 de Matemáticas III. Ecuaciones de grado superior a dos (bachillerato).
Unidad 4 de Matemáticas 3º grado, en vista de que esta unidad es de Graficación de Funciones.
Unidad 5 de Matemáticas III donde se analizarán diferentes casos de la recta. Ecuación de la Recta dados dos puntos por
donde pasa, dada su pendiente y un punto por el que pasa ; se analizan las condiciones particulares como paralelismo y
perpendicularidad.
ORIENTACION DE LOS TEMAS
Los conceptos deberán presentarse en relación directa con las ideas de variación proporcional y funciones lineales
tratadas en la unidad anterior, facilitando las relaciones entre funciones y ecuaciones de primer grado y además los casos
especiales de éstas.
Por supuesto, dichos conceptos no se presentarán de manera formal a través de definiciones rigurosas, sino situaciones
concretas cercanas al alumno para despertar su interés y atención sobre los tópicos que se abordan y de la utilidad
práctica de tales conocimientos.
Se tratarán problemas de introducción a las ecuaciones lineales, pasando por los diferentes casos particulares con algunos
casos sencillos de ecuaciones con paréntesis, se plantearán y solucionarán problemas que involucran a ecuaciones lineales.
9
Para el caso de ecuaciones con decimales y racionales, es conveniente que se aborde después de que los estudiantes hayan
comprendido las técnicas de solución en casos más simples.
Se deberá tomar en cuenta que el tema de ecuaciones lineales es conocido por los alumnos desde 2º de secundaria, por lo
que se deberán plantear las actividades que permitan revisar lo olvidado y dotar de sentido a los procedimientos
algebraicos tratados en esta unidad. (si trabajas con terceros grados)
NIVEL DE PROFUNDIDAD EN EL TRATAMIENTO DE LOS CONTENIDOS.
En esta unidad se pretenden aplicar, con ejemplos y ejercicios; los conceptos algebraicos y de forma general las variantes
en la reducción y operatoria del procedimiento para solucionar ecuaciones lineales, y, de esta manera conseguir que los
alumnos tengan habilidad en la manipulación de expresiones algebraicas.
Considerando que los alumnos ya han manejado los conceptos de ecuaciones, solución de ecuaciones; en esta unidad se deben
recordar y consolidar dichos conocimientos, dando oportunidad de que tengan sentido los procedimientos algebraicos y la
aplicación de los adquiridos en la unidad I correspondientes a variación proporcional, razones, proporciones y funciones
lineales.
PREVISIÓN DE OBSTÁCULOS DIDÁCTICOS
Generalmente los alumnos muestran dificultades debido a la inadecuada identificación de las operaciones involucradas en
una ecuación, y en consecuencia no obtienen la solución correcta. Por lo que es importante en esta unidad que el alumno
maneje de manera correcta dichos conceptos y de esta forma, prevenir errores como los siguientes:
a) 6x + 6y = 12xy
b) 6x + 7x2 = 13x 3
c) + 7 - 3 = - 4
d) - 9 - 4 = + 13
e) 6x = 0 dan como resultado x = - 6
10
f) 6x = 3 dan como resultado x = 3 - 6
La primera dificultad se debe a que no identifican las incógnitas ya que no les indican nada ni significan algo para que
puedan diferenciarlas; con relación a los signos, los alumnos están acostumbrados a repetir como receta la ley de
multiplicación de los signos por lo que no analizan ni interpretan correctamente las operaciones que se realizan, y
aplican a la adición de números la regla de multiplicación por lo que les es muy natural decir como en el ejemplo que (+7)
por (-3) da (- 4)
Otra de las dificultades es la determinación de la operación inversa en la transposición de términos, debido a que los
alumnos están acostumbrados al manejo de recetas para la solución de una ecuación, pero sin analizar las operaciones que
se realizan, por lo que se sugiere insistir en la transposición de términos con relación a la semejanza de la igualdad con
una balanza equilibrada.
Los alumnos no están acostumbrados a efectuar el análisis de un problema a fin de determinar la incógnita o incógnitas que
intervienen en el, por lo que en esta unidad se trata de que los alumnos puedan ir construyendo sus estrategias para
resolver y plantear problemas de manera algebraica.
SUGERENCIAS DIDÁCTICAS
Se iniciará con problemas sencillos, y que gradualmente se manejen otros de mayor complejidad, insistiendo en que es
fundamental poder expresar con facilidad los números y sus relaciones, para poder manejar de manera más adecuada y
sencilla los problemas de mayor generalidad.
Se sugiere que para empezar se realicen conversiones del lenguaje cotidiano al lenguaje algebraico, para posteriormente
insistir en las operaciones que se involucran, y después concluir en el manejo de las ecuaciones de primer grado con una
incógnita y su solución.
Con la finalidad de superar las dificultades de los alumnos
algebraico, fomentar el uso y significado de los paréntesis
tres actividades para que al terminar de realizar cada una,
manifestarán los alumnos. Esto puede manejarse también como
por traducir las expresiones cotidianas al lenguaje
para efectuar las operaciones de manera correcta; se proponen
el profesor aclare el porqué de los errores que seguramente
un examen de diagnóstico para el desarrollo del tema.
Como primera actividad se propone practicar la traducción al lenguaje algebraico. Se les indica a los alumnos expresiones
en lenguaje cotidiano y en álgebra, para que las relacione, en las expresiones, se señalan las operaciones básicas.
11
La segunda de las actividades consiste en realizar operaciones en donde se indican paréntesis y su efecto en la
representación de las expresiones algebraicas.
La tercera de las actividades tiene el objetivo de aclarar los diferentes elementos como coeficiente, exponente, número de
variables y grado de una expresión por lo que se sugiere se analicen dichos conceptos por medio del llenado de una tabla.
Para iniciar el desarrollo del tema, se propone empezar con un problema sencillo, en el que la solución prácticamente se
obtenga sin ningún problema y gradualmente se introduzcan problemas de mayor complejidad. A continuación, se presentan las
actividades como una muestra de los ejemplos que se pueden desarrollar.
ACTIVIDAD 1 LENGUAJE ALGEBRAICO
Para resolver eficientemente un problema en matemáticas, es fundamental poder expresar con facilidad los números con sus
relaciones, y poder realizar las manipulaciones correspondientes.
Lo primero que se debe hacer, para resolver un problema es traducir el problema del lenguaje cotidiano al lenguaje
algebraico, relaciona las siguientes columnas
Lenguaje cotidiano
Lenguaje algebraico
¸ a) 15 menos un número
(
) x / 15
¸ b) 15 unidades más que un número
(
) 2 (a + 15)
¸ c) 15 veces un número
(
) xy
¸ d) El cociente de 15 entre un número
(
) z + 15
¸ e) El cociente de dos números
(
) 15 - x
¸ f) El doble de la suma de a y 15
(
) x - 15
¸ g) El perímetro de un rectángulo
cuyos lados son a y 15
(
) 15 / x
¸ h) El producto de dos números
(
) 15 x - y
¸ i) El producto de x y 15
(
) x - y
¸ j) La diferencia de dos números
(
) y = x + 15
¸ k) La diferencia entre un número y 15 (
) P = 2a + 2(15)
¸ l) La quinceava parte de un número
) 15
(
12
¸ m) La suma de dos números
(
) 12x
¸ n) Un lado mide 15m mas que otro
(
) 15x
¸ o) Un número
(
) x + y
(
) x /y ó también x
y
(
) 15y
(
) x
(
) P = 2a + b
(
) x - 15
¸ p) Un número menos 15
¸ q) Una docena de x objetos
ACTIVIDAD 2
EVALUACIÓN DE EXPRESIONES ALGEBRAICAS
En una expresión algebraica, las variables representan números
El valor numérico de una expresión puede calcularse cuando a cada variable de la expresión se le asigna un valor
específico.
Se llama evaluación al proceso de calcular el valor numérico de una expresión.
Por ejemplo: Evaluar la expresión 2a + 2b
cuando : a = 5 y b = 7 Solución: 2( 5 ) + 2(7) =10+14 = 24 Respuesta : 24
cuando : a = -33 y b = 68 Solución: 2(-33)+2(68) = -66+136=70 Respuesta: 70
Evalúa las siguientes expresiones con los valores de:
13
a = 16, b = 12, c = 8, d = 24, e = 4
y relaciona con su valor:
a) a- b - (c (d / e))
(
) -10
b) (a -b)- (c d) /e
(
) -7
c) (a - (b - c
- d)) /e
(
) -3
d) ((a - b ) (c - d)) /e
(
) 2
e) (a - (b -c)
- d) /e
(
) 5
f) ((a - b -c)
- d) /e
(
) 6
g) a - (b -c (d / e))
(
) 8
h) a - (b -c) (d / e)
(
) 9
i) a - ((b -c d) / e)
(
) 18
j) (a - b - c)
- (d / e)
(
) 21
ACTIVIDAD 3
DETERMINACION DE VARIABLES Y GRADO DE LAS VARIABLES
Se considera conveniente antes de realizar operaciones con el fin de poder simplificar, y solucionar ecuaciones , es
necesario definir el grado de una variable, grado de un monomio y el grado de un polinomio. Por lo que se propone el
llenado y análisis de la siguiente tabla
14
Número de
Monomio
El grado de El grado del
Coeficiente
variables la variable
monomio
x2
35x3
35x2 y2
-87 x2 y3
-284x5 y3z2
2x
-287
40xy
5xy5
354
x
77x2 y3
17 x3 y3
27 x3 y3
EJEMPLOS DESARROLLADOS
Problema 1. Los organizadores de la fiesta para el día del estudiante, determinaron que los gastos serán de $525.00 y en
el grupo están dispuestos a cooperar solo 35 alumnos, ¿Cuánto debe cooperar cada uno de los alumnos?
¿Cuál ecuación representa el planteamiento del problema? 525 = 35x o 35x = 525
¿Cuál es la variable que hay que determinar y que nos da la solución del problema? x
¿Cuál es el valor de la variable ? x = 15
¿Cómo se obtuvo el valor de la variable ? X = 525 / 35
¿Es correcta la solución? si
¿Cómo se comprueba ? Sustituyendo el valor de 15 por la x en la ecuación 35x = 525 y comprobando que 35(15) = 525.
Problema 2. El costo del regalo para la mamá de Carlos es de $325.00 y lo van a comprar entre los 4 hermanos (3 y Carlos)
y el Papá que dijo que su aportación será de $125.00 ¿Cuánto debe cooperar cada uno de los 4 hermanos?
15
¿Cuál
¿Cuál
¿Cuál
¿Cómo
ecuación representa el planteamiento del problema? 4x + 125 = 325
es la variable que hay que determinar y que proporciona la solución del problema? x
es el valor de la variable ? x = 200/4 x = 50
se obtuvo el valor de la variable ? x = (325 - 125) / 4
PLANTEAMIENTO DE ECUACIONES
Problema 3. La suma de tres números es 123. El segundo número es el doble del primero y el tercero supera en tres al segundo.
Determinar los tres números.
1) ¿Cómo representas al primer número? _______________
2) ¿Cómo representas al segundo número? _____________
3) ¿Cómo representas al tercer numero? _______________
4) ¿Cómo representas que la suma de los tres es 123? ________
5) Determina los números, si la suma es 246. ___________ ________ __________
6) ¿Cuáles son los números si la suma es 63? __________ ________ __________
Problema 4. La anchura de un rectángulo es de x metros. ¿Cuál es el perímetro si su longitud fuera el doble del ancho?
1) ¿Cómo representas: su anchura? ___________________
2) ¿Cómo representas: su longitud es el doble del ancho? ____________
3) ¿Cómo representas: su perímetro? __________________ 4) ¿Cuál es el perímetro si su anchura es el triple del ancho?
____________
Problema
1) ¿Cómo
2) ¿Cómo
3) ¿Cómo
5. La tercera parte de un número es 5 unidades menor que la mitad de él. Encontrar el número.
representas: la tercera parte de un número? ___________________
representas: la mitad de este número? _______________________
representas: la tercera parte de un número es 5 unidades menor que la mitad del mismo? ___________________
Problema 6. Hallar dos números cuya suma sea 27 y que el séxtuplo del menor supere en 9 unidades al triple del mayor.
1) Número menor: x
2) Número mayor: 27 - x
16
3) Séxtuplo del menor supera en 9 unidades al triple del mayor: 6x = 9 + 3 (27- x)
4) ¿Cuáles son los números si la suma es 50?
Problema 7. Se realizan dos inversiones con un total de $15 000.00 . En la primera de las inversiones se tuvo un 8% de
utilidad, en la otra se perdió el 10%. Si la pérdida neta es de $600.00
¿Cuál es la cantidad de cada inversión?.
1) Primera inversión: x.
2) Segunda inversión: 15000 - x.
3) Ganancia: 8% x: 0.08x.
4) Pérdida: 10% (15000 - x): 0.10(15000 - x)
5) Pérdida menos ganancia igual perdida neta: 10%(15000 - x) - 8% x = 600: 0.10(15000 - x)-0.08x = 600
6) ¿Cuál es la cantidad de cada inversión, si en la primera se tuvo el 10% de utilidad. En la segunda el 12% de pérdida y
la pérdida neta es 540.00?
7) ¿Cuál es la cantidad de cada inversión si en la primera se tuvo 15% de utilidad, en la segunda 10% de pérdida y la
ganancia neta es $1000.00?
RESOLVER UNA ECUACIÓN
Problema 8. Encontrar el conjunto solución de la ecuación 3x= -14
Solución:
1) El coeficiente de x es 3 == 0
2) El inverso multiplicativo de 3 es
Se multiplican ambos miembros de la ecuación por
(3x)( ) =( )(-14)
1x = 14/3
4) Haz la comprobación.
Problema 9. Encuentra el conjunto solución de -6x = 0
Solución: Nota que el único número que multiplicado por -6 da cero es cuando x = 0
-6x = 0
El coeficiente de x es - 6
El inverso multiplicativo de - 6 es___________
( )( -6x) = ( )( 0 )
1x = 0
x = 0
Haz la comprobación.
17
Problema 10. Encuentra el conjunto solución de la ecuación
(5/7)x = 15
Solución :
El inverso multiplicativo de (5/7)
0 es 7/5
multiplicamos ambos miembros por el inverso multiplicativo
(7/5)(5x / 7) = (7/5) 15
1x = 7(15/5)
1x = 7(3)
1x = 21
x = 21
Comprueba la respuesta.
Problema 11. Resuelve la ecuación:
(2x /3) - (5/2) = (3/4) - (x/6)
Solución :
El mínimo común múltiplo de 3, 2, 4 y 6 es = 12
y como 12
0
multiplicamos ambos miembros de la ecuación por 12
12 {(2x / 3) - (5/2)} = 12{(3/4) - (x/6=
8x - 30 = 9 - 2x
El inverso aditivo de - 2x y de - 30 son + 2x y + 30
18
sumando en ambos miembros (2x + 30) 8x - 30 + (2x + 30) = 9 - 2x + (2x + 30)
8x + 2x + -30 + 30 = 9 - 2x + 2x + 30
10x = 39
El inverso multiplicativo de 10, que no es cero, es 1/10
multiplicando ambos miembros por 1/10 tenemos
(1/10) 10x = (1/10) 39
x = 3.9
ECUACIONES DE UNA SOLA VARIABLE
Encuentra el conjunto solución de las siguientes ecuaciones y comprueba el resultado
1.2.3.4.5.6.7.8.9.10.-
1.3x = -39
-6x = -12
(3x / 2) + (1/6) = ( 2x / 3) - (2/3)
(1x / 2) = 7
x/12 = 12
(x / -2) = 5
(1x / 6) = 1/9
(-1x / 3) = 1 / 81
(-x / 8) = 64
(2/3)x = 4
11.12.13.14.15.16.17.18.19.20.-
0.023x = 0.46
-0.7y = 2.1
(x/4) - (x/12) = (x/2) - (1/3)
x + (2/3) = 0
3x + 1
= 10
2 - 3x
= 11
2
- x
= 4
2(x + 4) + 7 = 19
3 - 2 ( 3x - 1 ) = 21
5 + 3( 2x + 1) = -1
SOLUCIÓN DE PROBLEMAS
Plantear y resolver los siguientes problemas.
1.- Un número es 4/5 de otro número y la suma de los dos es 126. Encuentre los números.
2.- La mitad de un número es igual a 2/5 del otro. Determinen los dos números si su suma es 27.
3.- El perímetro de un rectángulo es 60 metros cuadrados. Su longitud mide 4 metros más que su ancho. ¿Cuánto miden el
largo y el ancho?.
4.- Juan gasta $200 pesos a la semana en alimentos
¿Cuánto gastará a la semana si su precio aumenta el 10%?
19
5.- La longitud de un rectángulo mide 6 metros más que su ancho. Si el perímetro es de 96 metros. Encuentre las
dimensiones del rectángulo.
6.- Felipe tiene actualmente el cuádruplo de la edad de su hermano. Dentro de 15 años tendrá 3/2 de la correspondiente de
su hermano. ¿Cuál es la edad actual de Felipe?
EVALUACIÓN.
Proponemos que el profesor considere que tanto aprendieron los alumnos tomando como base las actividades iniciales de la
unidad y que actitudes, disposición y capacidades tiene para aplicar lo visto en la presente unidad, se recomienda que se
propicie la participación en equipos y grupal, para lo que se propone dejar ejercicios de tarea y un examen de una hora
para comprobar la habilidad en el método algebraico.
BIBLIOGRAFIA.
1) De OTEYZA /HERNANDEZ / LAM., Álgebra, Prentice Hall Hispanoamericana, S.A., México,1996.
2) GOBRAN, ALFONSE., Álgebra elemental, Grupo Editorial Iberoamérica, México.
3) LARSON / HOSTELLER., Álgebra, Publicaciones Cultural, México, 1996.
20
21
