Despeje de ecuaciones

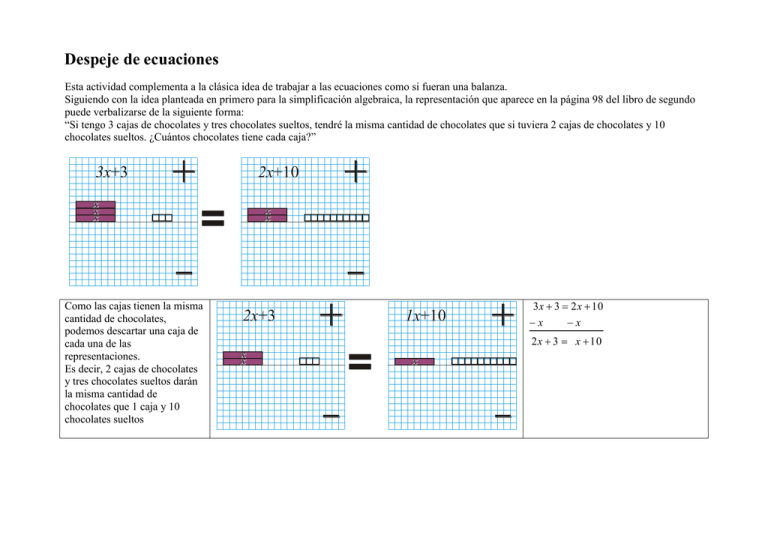
Despeje de ecuaciones
Esta actividad complementa a la clásica idea de trabajar a las ecuaciones como si fueran una balanza.
Siguiendo con la idea planteada en primero para la simplificación algebraica, la representación que aparece en la página 98 del libro de segundo
puede verbalizarse de la siguiente forma:
“Si tengo 3 cajas de chocolates y tres chocolates sueltos, tendré la misma cantidad de chocolates que si tuviera 2 cajas de chocolates y 10
chocolates sueltos. ¿Cuántos chocolates tiene cada caja?”
3x+3
2x+10
=
Como las cajas tienen la misma
cantidad de chocolates,
podemos descartar una caja de
cada una de las
representaciones.
Es decir, 2 cajas de chocolates
y tres chocolates sueltos darán
la misma cantidad de
chocolates que 1 caja y 10
chocolates sueltos
2x+3
1x+10
=
3x  3  2 x  10
x
x
2 x  3  x  10
Por la misma razón podemos
descartar una caja más de cada
una de las representaciones.
Es decir, 1 caja de chocolates y
tres chocolates dan un total de
10 chocolates
Finalmente quitamos 3
chocolates de cada
representación y obtenemos
que una caja tiene 7 chocolates.
x+3
10
7
=
x
x
x3 
=
x
2 x  3  x  10
10
x  3  10
3 3
x
7
La idea de esta representación es que el alumno visualice que para realizar un despeje se aplica la misma operación a ambos lados de la igualdad.
No es necesario que en este momento introduzca el nombre de despeje. Conviene que a la par que usted muestra la manipulación de las regletas
escriba el equivalente algebraico de cada uno de los pasos. Esta escritura será la que nos permita llegar a las reglas de despeje.
El ejercicio marcado como 1 en la página 98 tiene la intención de reforzar la idea de que no importa la operación que se realice, la igualdad sigue
siendo cierta siempre y cuando se realice a ambos lados de la igualdad.
Cuando resuelva el bloque de ejercicios I de la página 99 no pida a los alumnos que dibujen los procesos realizados con la regleta, esto llevará
mucho tiempo. Lo que ellos deben registrar son los pasos en forma algebraica: esto último requiere que hagan una traducción de los procesos de
la representación visual hacia el lenguaje algebraico. Poco a poco se darán cuenta de la utilidad de esta forma de representación.
Esperamos sus comentarios y sugerencias