G9B5C3 - Siplandi
Anuncio
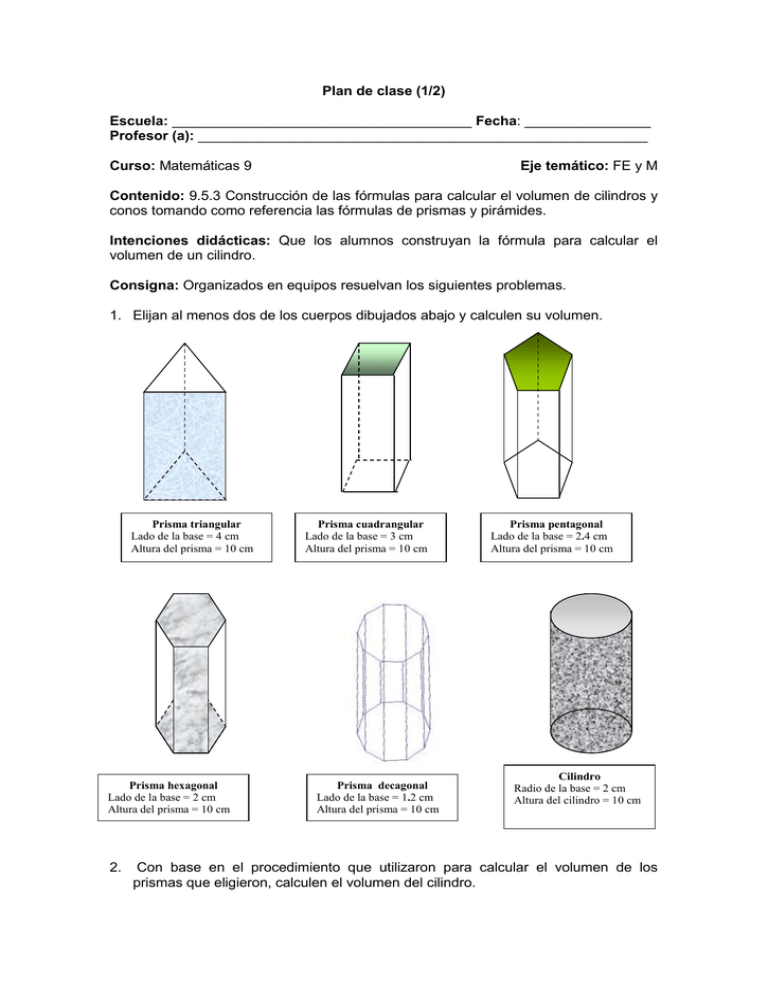
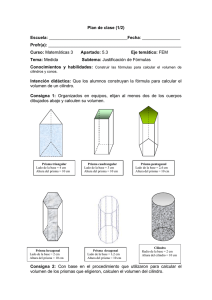
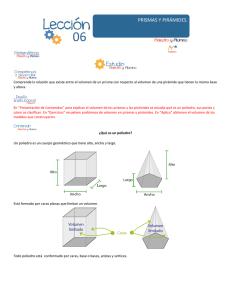
Plan de clase (1/2) Escuela: ______________________________________ Fecha: ________________ Profesor (a): _________________________________________________________ Curso: Matemáticas 9 Eje temático: FE y M Contenido: 9.5.3 Construcción de las fórmulas para calcular el volumen de cilindros y conos tomando como referencia las fórmulas de prismas y pirámides. Intenciones didácticas: Que los alumnos construyan la fórmula para calcular el volumen de un cilindro. Consigna: Organizados en equipos resuelvan los siguientes problemas. 1. Elijan al menos dos de los cuerpos dibujados abajo y calculen su volumen. Prisma triangular Lado de la base = 4 cm Altura del prisma = 10 cm Prisma hexagonal Lado de la base = 2 cm Altura del prisma = 10 cm 2. Prisma cuadrangular Lado de la base = 3 cm Altura del prisma = 10 cm Prisma decagonal Lado de la base = 1.2 cm Altura del prisma = 10 cm Prisma pentagonal Lado de la base = 2.4 cm Altura del prisma = 10 cm Cilindro Radio de la base = 2 cm Altura del cilindro = 10 cm Con base en el procedimiento que utilizaron para calcular el volumen de los prismas que eligieron, calculen el volumen del cilindro. Consideraciones previas: Anteriormente los alumnos calcularon y justificaron el volumen de prismas, por lo que se espera que sepan usar ese conocimiento, no sólo para calcular el volumen de los prismas elegidos, sino para inferir el procedimiento para calcular el volumen del cilindro. En los casos en los que se necesita la medida de la apotema, tendrán que recurrir al teorema de Pitágoras o a las razones trigonométricas para obtenerla. Si los alumnos tienen claro que el volumen de un prisma es igual al área de la base por la altura, es muy posible que vinculen este procedimiento con el volumen del cilindro. Una vez que haya quedado claro el procedimiento para calcular el volumen del cilindro conviene plantear las siguientes preguntas: ¿En cuál de los cuerpos dibujados se usa menos material para construirlo? ¿Cuál de los cuerpos dibujados tiene mayor volumen? Observaciones posteriores: 1. ¿Cuáles fueron los aspectos más exitosos de la sesión? _______________________________________________________________ _______________________________________________________________ _______________________________________________________________ 2. ¿Cuáles cambios considera que deben hacerse para mejorar el plan de clase? _______________________________________________________________ _______________________________________________________________ _______________________________________________________________ 3. Por favor, califique el plan de clase con respecto a su claridad y facilidad de uso para usted. Muy útil Útil Uso limitado Pobre Plan de clase (2/2) Escuela: ______________________________________ Fecha: ________________ Profesor (a): _________________________________________________________ Curso: Matemáticas 9 Eje temático: FE y M Contenido: 9.5.3 Construcción de las fórmulas para calcular el volumen de cilindros y conos tomando como referencia las fórmulas de prismas y pirámides. Intenciones didácticas: Que los alumnos construyan la fórmula para calcular el volumen del cono. Consigna: Organizados en equipos, hagan lo siguiente: a) Elijan al menos tres de las pirámides dibujadas y calculen su volumen Pirámide triangular Lado de la base = 4 cm Altura de la pirámide = 10 cm Pirámide hexagonal Lado de la base = 2 cm Altura de la pirámide = 10 cm Pirámide cuadrangular Lado de la base = 3 cm Altura de la pirámide = 10 cm Pirámide octagonal Lado de la base = 1.5 cm Altura de la pirámide = 10 cm Pirámide pentagonal Lado de la base = 2.4 cm Altura de la pirámide = 10 cm Pirámide dodecagonal Lado de la base = 1 cm Altura de la pirámide = 10 cm Pirámide de 20 lados Lado de la base = 0.6 cm Altura de la pirámide = 10 cm Cono Radio de la base = 2 cm Altura del cono = 10 cm b) Con base en el procedimiento que utilizaron para calcular el volumen de las pirámides elegidas, calculen el volumen del cono. Consideraciones previas: En las clases anteriores debió haber quedado clara la diferencia entre la generatriz y la altura en un cono, así como el hecho de que su base es un círculo. Con este trabajo también se espera que infieran la fórmula para calcular el volumen del cono, en el entendido de que el área de la base es πr2. Además, se puede recurrir al proceso de vaciado, para lo cual se requiere tener un cilindro y un cono construidos con cartoncillo o cartulina, con la misma base y altura, y algún material como arroz, lentejas, arena, etc., con la finalidad de comprobar la relación que existe entre los volúmenes de dichos sólidos. Observaciones posteriores: 1. ¿Cuáles fueron los aspectos más exitosos de la sesión? _______________________________________________________________ _______________________________________________________________ _______________________________________________________________ 2. ¿Cuáles cambios considera que deben hacerse para mejorar el plan de clase? _______________________________________________________________ _______________________________________________________________ _______________________________________________________________ 3. Por favor, califique el plan de clase con respecto a su claridad y facilidad de uso para usted. Muy útil Útil Uso limitado Pobre