PROGRAMACIÓN MÓDULO 1 - Universidad de Talca
Anuncio
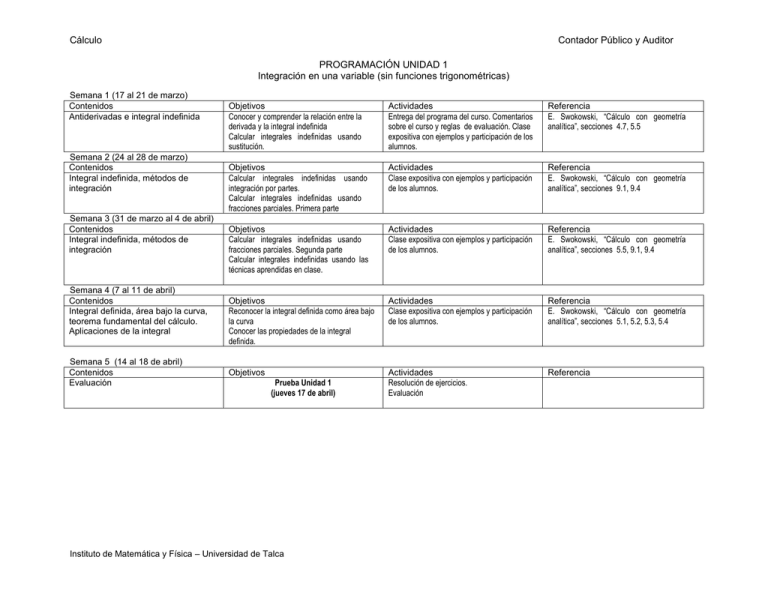
Cálculo Contador Público y Auditor PROGRAMACIÓN UNIDAD 1 Integración en una variable (sin funciones trigonométricas) Semana 1 (17 al 21 de marzo) Contenidos Antiderivadas e integral indefinida Semana 2 (24 al 28 de marzo) Contenidos Integral indefinida, métodos de integración Semana 3 (31 de marzo al 4 de abril) Contenidos Integral indefinida, métodos de integración Semana 4 (7 al 11 de abril) Contenidos Integral definida, área bajo la curva, teorema fundamental del cálculo. Aplicaciones de la integral Semana 5 (14 al 18 de abril) Contenidos Evaluación Objetivos Conocer y comprender la relación entre la derivada y la integral indefinida Calcular integrales indefinidas usando sustitución. Actividades Entrega del programa del curso. Comentarios sobre el curso y reglas de evaluación. Clase expositiva con ejemplos y participación de los alumnos. Referencia E. Swokowski, “Cálculo con geometría analítica”, secciones 4.7, 5.5 Objetivos Calcular integrales indefinidas usando integración por partes. Calcular integrales indefinidas usando fracciones parciales. Primera parte Actividades Clase expositiva con ejemplos y participación de los alumnos. Referencia E. Swokowski, “Cálculo con geometría analítica”, secciones 9.1, 9.4 Objetivos Calcular integrales indefinidas usando fracciones parciales. Segunda parte Calcular integrales indefinidas usando las técnicas aprendidas en clase. Actividades Clase expositiva con ejemplos y participación de los alumnos. Referencia E. Swokowski, “Cálculo con geometría analítica”, secciones 5.5, 9.1, 9.4 Objetivos Reconocer la integral definida como área bajo la curva Conocer las propiedades de la integral definida. Actividades Clase expositiva con ejemplos y participación de los alumnos. Referencia E. Swokowski, “Cálculo con geometría analítica”, secciones 5.1, 5.2, 5.3, 5.4 Objetivos Actividades Resolución de ejercicios. Evaluación Referencia Prueba Unidad 1 (jueves 17 de abril) Instituto de Matemática y Física – Universidad de Talca Cálculo Contador Público y Auditor PROGRAMACIÓN UNIDAD 2 Funciones de Varias Variables Semana 6 (21 al 25 de abril) Contenidos Funciones de varias variables Semana 8 (5 al 9 de mayo) Contenidos Derivación en varias variables Planos tangentes a superficies Semana 9 (12 al 16 de mayo) Contenidos Regla de la Cadena Gradientes y planos tangentes Semana 10 (19 al 23 de mayo) Contenidos Máximos y mínimos de funciones de dos variables Semana 11 (26 al 30 de mayo) Contenidos Máximos y mínimos de funciones de dos variables. Multiplicadores de Lagrange Semana 12 (2 al 6 de junio) Contenidos Evaluación Objetivos Conocer las funciones de varias variables, su representación gráfica. Aprender a trazar curvas de nivel Actividades Clase expositiva con ejemplos y participación de los alumnos. Referencia E. Swokowski, “Cálculo con geometría analítica”, sección 16.1 Objetivos Aprender a calcular derivadas parciales y a interpretarlas. Calcular derivadas parciales de orden superior Conocer el teorema sobre la igualdad de las derivadas mixtas Calcular planos tangentes a una superficie. Actividades Clase expositiva con ejemplos y participación de los alumnos. Referencia E. Swokowski, “Cálculo con geometría analítica”, secciones 16.3, 16.5 Objetivos Conocer y aprender a usar la regla de la cadena. Calcular las rectas tangentes a curvas sobre superficies. Actividades Clase expositiva con ejemplos y participación de los alumnos. Referencia E. Swokowski, “Cálculo con geometría analítica”, secciones 16.8 Objetivos Conocer los criterios de la primera y segunda derivadas pare determinar extremos relativos de funciones de dos variables a través de los puntos críticos. Actividades Clase expositiva con ejemplos y participación de los alumnos. Referencia E. Swokowski, “Cálculo con geometría analítica”, secciones 5.3, 5.4 Objetivos Aprender a calcular los máximos y mínimos sujetas a restricciones (en un dominio con “borde” o frontera). El método de los multiplicadores de Lagrange. Actividades Clase expositiva con ejemplos y participación de los alumnos. Referencia E. Swokowski, “Cálculo con geometría analítica”, secciones 6.1 Objetivos Actividades Resolución de ejercicios Evaluación Referencia Prueba Unidad 2 (jueves 5 de junio) Instituto de Matemática y Física – Universidad de Talca Cálculo Contador Público y Auditor PROGRAMACIÓN UNIDAD 3 Ecuaciones diferenciales Semana 13 (9 al 13 de junio) Contenidos Introducción a las ecuaciones diferenciales Objetivos Conocer las primeras herramientas para calcular ecuaciones diferenciales. Actividades Clase expositiva con ejemplos y participación de los alumnos. Referencia E. Swokowski, “Cálculo con geometría analítica”, sección 19.1 Semana 14 (16 al 20 de junio) Contenidos Ecuaciones diferenciales de variables separables. Objetivos Calcular los tipos más simple de ecuaciones diferenciales. Actividades Clase expositiva con ejemplos y participación de los alumnos. Referencia E. Swokowski, “Cálculo con geometría analítica”, secciones 19.2, Semana 15 (23 al 27 de junio) Contenidos Ecuaciones diferenciales Homogéneas Objetivos Calcular los tipos más simple de ecuaciones diferenciales. Actividades Clase expositiva con ejemplos y participación de los alumnos. Referencia E. Swokowski, “Cálculo con geometría analítica”, secciones 19.3, Semana 16 (30 de junio al 4 de julio) Contenidos Ecuaciones diferenciales exactas. Ecuaciones diferenciales lineales. Objetivos Calcular los tipos más simple de ecuaciones diferenciales. Actividades Clase expositiva con ejemplos y participación de los alumnos. Referencia E. Swokowski, “Cálculo con geometría analítica”, secciones 19.4, Objetivos Actividades Resolución de ejercicios Evaluación Referencia Semana 17 (7 al 11 de julio) Contenidos Evaluación Prueba Unidad 3 (jueves 10 de julio) Instituto de Matemática y Física – Universidad de Talca



