SEGUNDO BARQUIEXAMEN

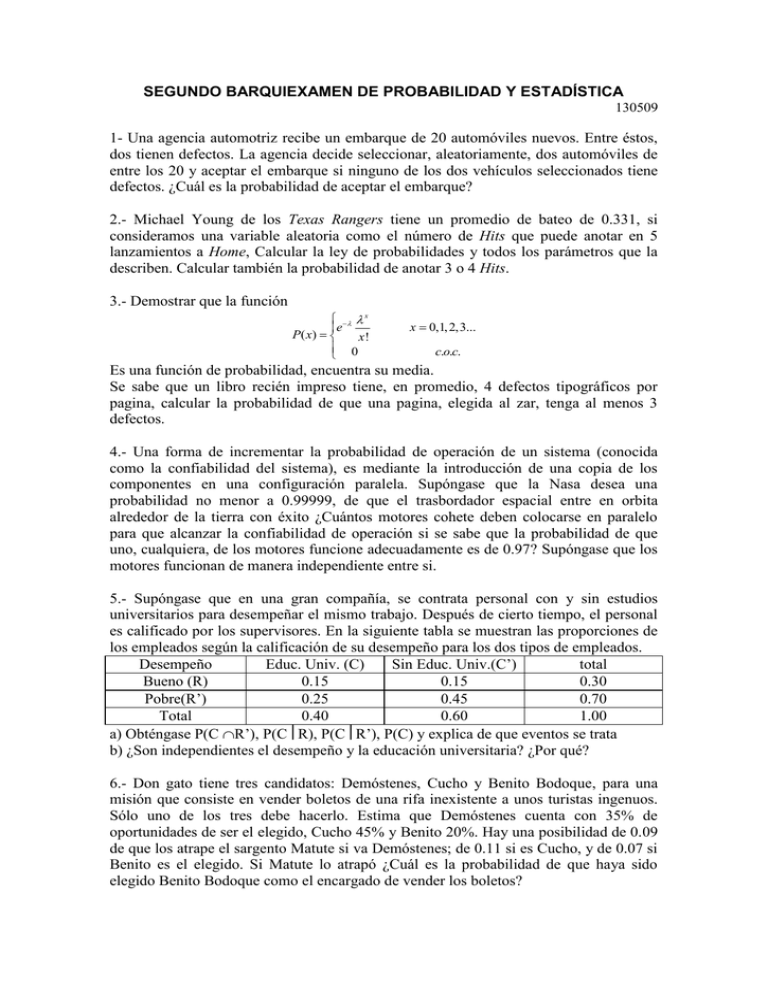
SEGUNDO BARQUIEXAMEN DE PROBABILIDAD Y ESTADÍSTICA
130509
1- Una agencia automotriz recibe un embarque de 20 automóviles nuevos. Entre éstos,
dos tienen defectos. La agencia decide seleccionar, aleatoriamente, dos automóviles de
entre los 20 y aceptar el embarque si ninguno de los dos vehículos seleccionados tiene
defectos. ¿Cuál es la probabilidad de aceptar el embarque?
2.- Michael Young de los Texas Rangers tiene un promedio de bateo de 0.331, si
consideramos una variable aleatoria como el número de Hits que puede anotar en 5
lanzamientos a Home, Calcular la ley de probabilidades y todos los parámetros que la
describen. Calcular también la probabilidad de anotar 3 o 4 Hits.
3.- Demostrar que la función
   x
e
P( x)  
x!
 0

x  0,1, 2,3...
c.o.c.
Es una función de probabilidad, encuentra su media.
Se sabe que un libro recién impreso tiene, en promedio, 4 defectos tipográficos por
pagina, calcular la probabilidad de que una pagina, elegida al zar, tenga al menos 3
defectos.
4.- Una forma de incrementar la probabilidad de operación de un sistema (conocida
como la confiabilidad del sistema), es mediante la introducción de una copia de los
componentes en una configuración paralela. Supóngase que la Nasa desea una
probabilidad no menor a 0.99999, de que el trasbordador espacial entre en orbita
alrededor de la tierra con éxito ¿Cuántos motores cohete deben colocarse en paralelo
para que alcanzar la confiabilidad de operación si se sabe que la probabilidad de que
uno, cualquiera, de los motores funcione adecuadamente es de 0.97? Supóngase que los
motores funcionan de manera independiente entre si.
5.- Supóngase que en una gran compañía, se contrata personal con y sin estudios
universitarios para desempeñar el mismo trabajo. Después de cierto tiempo, el personal
es calificado por los supervisores. En la siguiente tabla se muestran las proporciones de
los empleados según la calificación de su desempeño para los dos tipos de empleados.
Desempeño
Educ. Univ. (C)
Sin Educ. Univ.(C’)
total
Bueno (R)
0.15
0.15
0.30
Pobre(R’)
0.25
0.45
0.70
Total
0.40
0.60
1.00
a) Obténgase P(C R’), P(CR), P(CR’), P(C) y explica de que eventos se trata
b) ¿Son independientes el desempeño y la educación universitaria? ¿Por qué?
6.- Don gato tiene tres candidatos: Demóstenes, Cucho y Benito Bodoque, para una
misión que consiste en vender boletos de una rifa inexistente a unos turistas ingenuos.
Sólo uno de los tres debe hacerlo. Estima que Demóstenes cuenta con 35% de
oportunidades de ser el elegido, Cucho 45% y Benito 20%. Hay una posibilidad de 0.09
de que los atrape el sargento Matute si va Demóstenes; de 0.11 si es Cucho, y de 0.07 si
Benito es el elegido. Si Matute lo atrapó ¿Cuál es la probabilidad de que haya sido
elegido Benito Bodoque como el encargado de vender los boletos?
7.- Una agencia automotriz recibe un embarque de 20 automóviles nuevos. Entre éstos,
dos tienen defectos. La agencia decide seleccionar, aleatoriamente, dos automóviles de
entre los 20 y aceptar el embarque si ninguno de los dos vehículos seleccionados tiene
defectos. ¿Cuál es la probabilidad de aceptar el embarque?
8.- Hallar la función de distribución acumulada, la media, la varianza, la desviación
estándar, el sesgo, la curtosis, sesgo estandarizado, curtosis estandarizada, coeficiente
de variación, moda y mediana, de la siguiente función:
16 xe4 x
x0
f ( x)  
c.o.c
 0
9.- Encuentra la función de probabilidad del lanzamiento de dos dados distinguibles,
siendo la variable aleatoria la diferencia de sus caras, y halla la función de distribución
acumulada, la media, la varianza, la desviación estándar, el sesgo, la curtosis, sesgo
estandarizado, curtosis estandarizada, coeficiente de variación, moda y mediana.
10.- Una agencia de renta de automóviles recibe 0, 1, 2, 3, 4, o 5 autos que le regresan
cada día, con probabilidades de 1/6, 1/6, 1/3, 1/12, 1/6 y 1/12 respectivamente.
Encuentra la media, moda, mediana, varianza, desviación estándar, Coeficiente de
variación, sesgo, sesgo estandarizado, curtosis, curtosis estandarizada y función de
distribución acumulada.
x0
1 / 3
2 / 3
x 1
Sea P( x)  

c.o.c
0
Encuentra la media, moda, mediana, varianza, desviación estándar, Coeficiente
de variación, sesgo, sesgo estandarizado, curtosis, curtosis estandarizada y función de
distribución acumulada.
11.- Demuestra que para la siguiente función de densidad de probabilidad:
 1
a xb

f ( x)   b  a

c.o.c
 0
la curtosis estandarizada es independiente del intervalo donde se define la función.
12.- Van a bailar m mujeres y n hombres, ¿De cuántas maneras pueden formarse todas
las posibles k parejas para bailar? (k ≤ min[m, n])