CALCULO DIFERENCIAL E INTEGRAL DE UNA VARIABLE
Anuncio
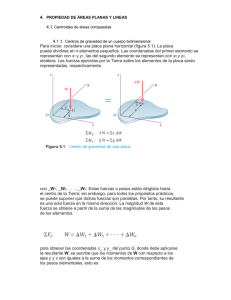
CALCULO DIFERENCIAL E INTEGRAL DE UNA VARIABLE Semana 13 Clase 1 1 HABILIDAD Calcula la fuerza ejercida por un líquido sobre un extremo de un depósito. 2 Calcula Momentos y Centroides Calcula Momentos de Inercia 3 ACTIVIDADES 1. Hacer una explicación previa de presión, fuerza hidrostática, como aparece en la página 555. 2. Explicar los ejemplos 1 y 2 de la sección 8.3. 1. Describe el concepto de centro de masa (pag 557) 2. Calcula el centro de masa de un sistema de partículas respecto a x e y (pag 558) 3. Explica como “cortar en pedazos” una placa delgada uniforme para calcular su centroide. 4. Explica que el centroide coincide con el Centro de Areas en este caso. 5. Explica como hallar dMx y dMy. NO APLICAR LAS FORMULAS DEL LIBRO. 6. Indica las fórmulas para hallar el Centroide de una placa delgada uniforme y resuelve los Ejemplos 4 y 5. 7. Indica como trabajar la región si está comprendida entre dos curvas (pag561) y resuelve el Ejemplo 7. 1. Explica que el concepto de Momento de Inercia de una placa delgada uniforrme es llamado segundo momento y que se calcula a nivel diferencial como dIx = y 2 dA y dIy = 2 x dA. 2. Indica que el cálculo es análogo al de los momentos para calcular centroide. EJERCICIOS Sección 8.3 Problemas: 1,2,.....,15. Se recomienda que los alumnos resuelvan en clase 3,5,7,9. Ejercicios en hoja aparte. Este tema este ciclo no se hará. Ejercicios en hoja aparte. Clase 2 1 Determina el área de una región limitada por curvas en coordenadas polares. 1. Describir los elementos del sistema coordenado polar este tema se desarrollo en MB. 2. Graficar algunas ecuaciones en coordenadas polares. Se sugiere hacer r cons tan te y constante . Considerar solamente r 0 . 1 CALCULO DIFERENCIAL E INTEGRAL DE UNA VARIABLE 3. Explicar la forma en que se transforma ecuaciones de xy a r y viceversa. 4. Explicar la forma de graficar ciertas ecuaciones tales como r asen , r a cos , r 2 2 cos , r cos 2 5. Explicar a los alumnos la forma en que se determina los puntos de intersección de curvas en coordenadas polares. 6. Explicar el elemento diferencial (ahora es un sector circular). 7. Luego establecer la integral definida que permita hallar el área solicitada. CLASE 3 Clase Práctica: 1 Trabajo con problemas de modelación abordados en la semana. Calcula áreas en coordenadas polares. 2
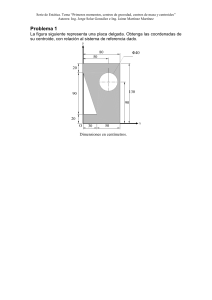

![Transforma la integral / (x2 " y2) dx ] dy a coordenadas polares y](http://s2.studylib.es/store/data/005336881_1-38107913b0406391f278007c215c7e11-300x300.png)