mtodos de levantamiento-1

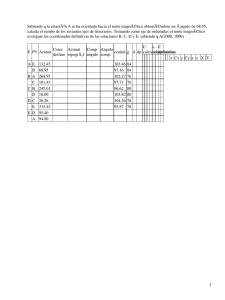
Métodos de Levantamiento
• ANGULOS
Los ángulos que se miden en topografía se clasifican
en horizontales o verticales, dependiendo del plano en
que se midan. Los ángulos horizontales son las
medidas básicas que se necesitan para determinar
rumbos y acimut. Los ángulos verticales (o cenitales)
se usan en la nivelación trigonométrica, en estadía y
para reducir distancias inclinadas con respecto a la
horizontal.
* Condiciones básicas para determinar un ángulo.
Existen tres condiciones básicas que determinan un
ángulo. Como se muestra en la figura, éstas son: (1) la
línea de referencia, (2) el sentido del giro, y (3) la
amplitud. Los métodos para calcular rumbos y acimut
que se describen en este capítulo se basan en esos
tres elementos.
•
•
UNIDADES DE MEDIDA ANGULAR
Una unidad puramente arbitraria define el valor de un ángulo. El sistema
sexagesimal que se utiliza comúnmente se basa en las unidades llamadas
grados, minutos y segundos y las subdivisiones decimales de dichas
unidades. En Europa se emplea normalmente el grado centesimal . Los
radianes pueden ser más prácticos en los cálculos y, de hecho, se
emplean extensamente en las computadoras electrónicas
CLASES DE ÁNGULOS HORIZONTALES
Los ángulos horizontales que se miden más a menudo en topografía son:
(1) ángulos interiores, (2) ángulos a la derecha, y (3) ángulos de deflexión.
* Los ángulos interiores, que se muestran en la figura , son los ángulos
que quedan dentro de un polígono cerrado. Normalmente se mide el
ángulo en cada vértice del polígono. Luego, puede efectuarse una
verificación de los valores obtenidos, dado que la suma de todos los
ángulos en cualquier polígono debe ser igual a (n - 2)180°, donde n es el
número de ángulos.
* Los ángulos exteriores, que quedan fuera del polígono cerrado,
son suplementos a 360° de los ángulos interiores. Raras veces
resulta ventajoso medir estos ángulos, a no ser que se trate de
una comprobación, ya que la suma de los ángulos interiores y
exteriores en cualquier estación debe ser igual a 360°.
* Los ángulos de deflexión ,se miden ya sea hacia la derecha
(el sentido de las manecillas se considera positivo) o hacia la
izquierda (sentido opuesto de las manecillas, considerado
como negativo), a partir de la prolongación de la línea de atrás
y hacia la estación de adelante. Los ángulos de deflexión son
siempre menores de 180° y el sentido de giro se define
anexando una D o una / al valor numérico. Así, el ángulo en B
en la figura es derecho (D) y el ángulo en C es izquierdo (/).
• RUMBOS
Los rumbos representan un sistema para designar las
direcciones de las líneas. El rumbo de una línea es el ángulo
agudo horizontal entre un meridiano de referencia y la línea.
El ángulo se mide ya sea desde el Norte o desde el Sur, y
hacia el Este o el Oeste, y su valor no es mayor de 90°. El
cuadrante en el que se encuentra se indica comúnmente con
la letra N o la S precediendo al valor numérico del ángulo, y la
letra E o la W, después de dicho valor. Así, la expresión
correcta de un rumbo debe incluir letras de cuadrante y un
valor angular; por ejemplo: N80°E.
• ACIMUT
Es un ángulo horizontal medido en sentido de las manecillas desde
cualquier meridiano de referencia. En topografía plana, el acimut se
mide generalmente a partir del Norte, pero a veces se usa el Sur
como dirección de referencia
Los acimut pueden leerse directamente en el círculo graduado de
un instrumento de estación total, de un teodolito repetidor después
de haber orientado adecuadamente el instrumento. Esto puede
hacerse visando a lo largo de una línea de acimut conocido, con
dicho ángulo marcado en el círculo, y girando luego a la dirección
deseada.
• Calculo de Acimut
Muchos topógrafos prefieren los acimut a los rumbos para fijar las
direcciones de las líneas, porque es más fácil trabajar con ellos,
especialmente cuando se calculan poligonales empleando computadoras
electrónicas. Los senos y los cosenos de los ángulos acimutales dan
automáticamente los signos algebraicos correctos para las proyecciones
meridianas y paralelas.
Los cálculos de acimut, como los de rumbos, se hacen mejor con ayuda de
un esquema. La figura muestra los cálculos para el acimut de BC de la
figura a). El acimut de AB se obtiene sumando 180° al acimut de BA: 180°
+ 41°35' = 221°35'. Luego, el ángulo positivo en B, de 129°11', se suma al
acimut de BA para tener el de BC igual a 221º35' + 129°11' = 350°46'.
Este proceso general de sumar (o de restar) 180° para obtener el acimut
inverso y luego sumar el ángulo horario se repite para cada línea hasta que
se recalcula el acimut de la línea de inicio. Si un acimut o un acimut inverso
calculado excede de 360°, se restan 360° del valor obtenido y se prosiguen
los cálculos.
ESQUEMA DE ACIMUTS