2DO LOGICA (1)
Anuncio

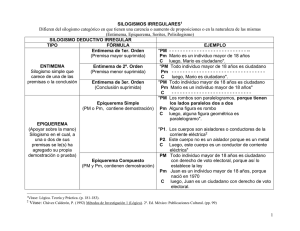
PLANEACION BIMESTRAL ASIGNATURA: LOGICA FECHA: ABRIL - JUNIO GRADO: B201 DOCENTE: L.C.H Areli Talavera Castañeda LOS PRIMEROS PRINCIPIOS EL RACIOCINIO EL SILOGISMO FORMA DEL SILOGISMO FIGURAS DEL SILOGISMO SILOGISMOS ESPECIALES LA INDUCCIÒN TRABAJO EN CUADERNO FRASE: “Ser excelente es comprender que la vida no es algo que se nos da hecha, sino que tenemos que producir las oportunidades para alcanzar el éxito” VALOR: Responsabilidad FRASE: “Ser excelente es comprender que, con base a una férrea disciplina, es factible forjar un carácter de triunfador” VALOR: Respeto FRASE: “Ser excelente es trazarse un plan y lograr los objetivos deseados a pesar de todas las circunstancias” VALOR: Confianza 1. OBJETIVO.1: Que el alumno logre realizar un proceso sistematico en una investigación. 2: hacer un uso correcto de las herramientas de búsqueda. 3: que el alumno use habilidades para relacionar la información y aplicarla a un tema determinado. Contenido científico LOS PRIMEROS PRINCIPIOS Los “principios lógicos” constituyen las verdades primeras, “evidentes” por sí mismas, a partir de las cuales se construye todo el edificio formal del pensamiento, según la Lógica tradicional. Dentro de una consideración más moderna de la Lógica Formal, los principios lógicos serán los preceptos o reglas “operantes” que rigen toda forma correcta de pensamiento. El modo de considerar estos principios ha variado a través de la Historia de la Lógica y del pensamiento científico, pero la Lógica Formal ha coincidido en la formulación de cuatro principios lógicos, aunque el cuarto no es aceptado por todos los lógicos. Tales principios son: 1. Principio de identidad. 2. Principio de Contradicción (o Principio de no-Contradicción). 3. Principio de Exclusión del término medio (o Principio del medio excluido o Principio del tercero excluido o Principio del Tercer término excluido) 4. Principio de Razón Suficiente. Desde un punto de vista psicológico (aunque no desde la Psicología Científica sino de la Psicología Racional), los principios lógicos serían las leyes generales de “operación del pensamiento”, es decir, las leyes que fundamentan los procesos lógicos. Desde un punto de vista ontológico o metafísico, estos principios serían las determinaciones más generales del “ser” aún más generales que las categorías. Pero desde un punto de vista estrictamente lógico, sólo pueden ser considerados como las proposiciones fundamentales que cimientan toda otra proposición en el pensamiento “formalmente” correcto. EL PRINCIPIO DE IDENTIDAD. El principio de Identidad fue formulado por primera vez como parte de una teoría de la realidad del “ser”. Ese principio afirmaba algo tan general como que “El ‘ser’ es”; esto puede ser explicado diciendo que “todo objeto es idéntico a sí mismo”. Estas afirmaciones no son todavía lógicas, pero con el tiempo, se reflexiono sobre las implicaciones lógicas de ese principio, logrando la formulación lógico-formal del primer principio. Esa formulación consistió en la afirmación de la verdad de un juicio cuyo objeto sea idéntico al predicado (ese tipo de juicio se ha llamado “juicio analítico”). El primer principio lógico se ha resumido con la fórmula: “A es A” EL PRINCIPIO DE CONTRADICCIÓN. Este principio ha sido llamado tradicional e incorrectamente “principio de contradicción”, cuando lo que se enuncia es la imposibilidad de contradicción en el pensamiento. Se trata del principio fundamental de la Lógica clásica que descarta cualquier posibilidad de contradicción en el pensamiento y en la realidad (esta implicación ha sido y es uno de los obstáculos más fuertes que ha encontrado toda consideración dialéctica de la realidad y el pensamiento). La forma más plena del segundo principio es la que se refiere a la no-contradicción entre dos juicios, tal como se expresa en la fórmula: “’A es A’ y ‘A no es A’ no son ambos verdaderos” que se lee: El juicio ‘A es A’ y su contradictorio, el juicio ‘A no es A’ no pueden ser verdaderos a la vez.La forma original de este segundo principio es también ontológica y se formulaba de la siguiente manera: “El ser es y no puede a la vez no ser”. EL PRINCIPIO DE EXCLUSIÓN DEL TÉRMINO MEDIO. Como un complemento necesario del principio de no contradicción, se formula el principio de exclusión del término medio. En su forma original, se refería también a una estructura de la realidad y consistía en la afirmación de que no hay término medio entre el “ser” y el “no-ser”. En su forma lógica, este principio debe entenderse como afirmando que dos juicios contradictorios no pueden ser ambos falsos, tal como se sintetiza en al fórmula: “’A es A’ y ‘A no es A’ no son ambos falsos”que se lee: El juicio ‘A es A’ y su contradictorio, el juicio ‘A no es A’ no pueden ser falsos a la vez. EL PRINCIPIO DE RAZÓN SUFICIENTE. Este es, de los cuatro principios lógicos, el más discutido, pues no todos los lógicos clásicos lo acepten. Su formulación fue muy posterior a la de los otros, pues mientras los primeros tres se atribuyen a Parménides de Elea –quien vivió en el siglo V antes de nuestra era-, el cuarto principio fue formulado por Gottfried Wilhelm Leibniz aproximadamente en 1666, en plena Edad Moderna. El cuarto principio se enuncia: “Nada es sin una razón suficiente”. Christian Wolf en 1712 distinguió entre tres modos de entender este principio: a) Como “razón de ser”, b) Como “razón de llegar a ser” c) Como “razón de conocer”. Dentro de la Lógica tradicional, se ha entendido este cuarto principio en el tercero de los significados que propuso Wolf. Desde ese punto de vista, el principio puede ser formulado: “Todo conocimiento tiene que estar fundado”. EL RACIOCINIO Esta es la tercer foma mental: La razón es la facultad en virtud de la cual el ser humano es capaz de identificar conceptos, cuestionarlos, hallar coherencia o contradicción entre ellos y así inducir o deducir otros distintos de los que ya conoce. Así, la razón humana, más que descubrir certezas es una capacidad de establecer o descartar nuevos conceptos concluyentes o conclusiones, en función de su coherencia con respecto de otros conceptos de partida o premisas. Los más conocidos y utilizados de manera cotidiana, y en asiganturas como: Métodos y Pensamiento Crítico son: Razonamiento deductivo:La filosofía de Aristóteles y Platón engendró la lógica primaria, que era deductiva y no inductiva. Esto quiere decir que las leyes universales podían ser descubiertas por el pensamiento humano sin necesidad que éste tuviese que optar por mirar casos particulares para establecer las leyes. Es decir, la lógica deductiva discurre sobre lo que sigue universalmente desde premisas dadas por la razón humana. Es esta la razón por la cual Aristóteles estableció los cuatro principios a priori para la lógica todavía enseñados en nuestra época: el principio de identidad, el principio de no contradicción, el principio del tercero excluido y el principio de razón suficiente.[1] Sin embargo, el hacer uso únicamente de la lógica deductiva puede llevar a errores, ya que se deja la observación de casos particulares de lado, para ver si se verifica el razonamiento. Así, Aristóteles se equivocó incluso en el número de dientes que tenían las mujeres, habiéndose podido enterar simplemente observando y contando. En oposición al mero formalismo lógico los idealistas, y en especial Hegel, consideraron de otra forma el principio de contradicción en cuanto a lo Universal moral como "praxis" o conceptual y teórico. Propusieron el método dialéctico para partir de la materia concreta dada para llegar a la forma de abstracciones universales y luego proponer definiciones generales. El análisis deja lo concreto como fundamento y por medio de la abstracción de las particularidades, que aparentan ser inesenciales, pone de relieve lo universal concreto o sea la fuerza de ley general. Es ir de lo general a lo particular. Razonamiento inductivo: (ahora es de lo particular a lo general )En el mismo sentido, el razonamiento inductivo, es el estudio de derivar una generalización o una ley a partir de observaciones. Éste fue posteriormente incluido en el estudio de la lógica, y fue adoptado como el razonamiento básico de la investigación científica, combinándola cuando corresponde con la deducción. Este probablemente es el motivo del éxito y la certeza de los modelos científicos actuales. Es decir, la inclusión del razonamiento inductivo en las ciencias no es menor en nuestras vidas, nos permitió tener el modelo científico actual el cual nos ha dado una cantidad impresionante de tecnología y supuestas “verdades”. En la ciencia moderna, el razonamiento inductivo basa sus conclusiones en las inferencias estadísticas. Es decir, se toma o registran una cantidad de datos sobre un fenómeno y se establecen conclusiones basadas en modelos probabilísticos, en la mayoría de los casos siguiendo la curva normal, acerca del fenómeno estudiado. La base filosófica del razonamiento inductivo la encontramos en el principio de razón suficiente, desarrollado, entre otros, por Leibniz. Un concepto que vamos a utilizar casi como sinónimo para el razonamiento es el de Inferencia Inferir: Es el proceso por el cual se obtinen nuevos conociemientos a partir de los que ya se tienen viejo conocimiento se infiere un Nuevo conocimiento INFERENCIAS LOGICAS: Hay dos tipos principalmente y que vamos a trabajar (ver mapa para mayor información) Inferencia Mediata e Inferencia Inmediata Inferencias inmediatas: ]La filosofía tradicional aristotélica consideraba la posibilidad de inferencias inmediatas: aquellas que pueden obtenerse directamente a partir de la relación que establece un juicio[7] respecto a los términos, sujeto y predicado, que le constituyen, en función de la cualidad (afirmativo-negativo) y la cantidad (universal-particular) del mismo. Aristóteles estudió con detalle ciertas operaciones que permitían tales inferencias inmediatas o directas. Para ello elaboró el llamado cuadro de oposición de los juicios, en el que dadas las relaciones que cada juicio aristotélico, A,E,I,O, lleva implícitas se pueden establecer ciertas inferencias directas. Artículo principal: Cuadro de oposición de los juicios Asimismo en la lógica tradicional se admitían ciertas operaciones lógicas de transformación de un juicio manteniendo sus condiciones de verdad. Tales operaciones eran: Conversión lógica Obversión lógica Contraposición lógica Inversión lógica Artículo principal: Silogismo Problemática de la lógica aristotélica La lógica actual formaliza los enunciados lingüísticos bien como relación de clases o como funciones proposicionales o relaciones.[9] Hoy se exige el rigor formal de la aplicación de una regla de inferencia.[10] La idea de inferencia inmediata no es más que la aplicación de una regla modo implícito. La formalidad lógica, sin embargo, exige que sea explícita la regla que permite la transformación de una EBF Inferencias Mediatas: Son aquellas que se obtienen de varias premisas EL SILOGISMO El silogismo es una forma de razonamiento deductivo que consta de dos proposiciones como premisas y otra como conclusión, siendo la última una inferencia necesariamente deductiva de las otras dos. Fue formulado por primera vez por Aristóteles, en su obra lógica recopilada como El Organon, de sus libros conocidos como Primeros Analíticos, (en griego Proto Analytika, en latín – idioma en el que se conoció la obra en Europa Occidental-, Analytica Priora). Aristóteles consideraba la lógica como lógica de relación de términos. Los términos se unen o separan en los juicios. Los juicios aristotélicos son considerados desde el punto de vista de unión o separación de dos términos, un sujeto y un predicado. Hoy se hablaría de proposición. La diferencia entre juicio y proposición es importante. La proposición afirma un hecho como un todo, que es o no es, como contenido lógico del conocimiento. El juicio, en cambio, atribuye un predicado a un sujeto lógico del conocimiento otorgando a los términos al mismo tiempo una función lingüística de significado (semántica) y una función formal lógica (sintáctica). Esto tiene su importancia en el concepto mismo del contenido de uno, el juicio, y la otra, la proposición, especialmente en los casos de negación, como se considera, más adelante, en la problemática de la lógica silogística. Mantenemos aquí la denominación de juicio por ser lo más acorde con lo tradicional, teniendo en cuenta que este tipo de lógica, como tal, está en claro desuso, sustituida por la lógica simbólica en la que esta lógica es interpretada como lógica de clases. Ver cálculo lógico. La relación entre los términos de un juicio, al ser comparado con un tercero que hace de "término medio", hace posible la aparición de las posibles conclusiones. Así pues, el silogismo consta de dos juicios, premisa mayor y premisa menor, en los que se comparan tres términos, de cuya comparación se obtiene un nuevo juicio como conclusión. La lógica trata de establecer las leyes que garantizan que, de la verdad de los juicios comparados (premisas), se pueda obtener con garantía de verdad un nuevo juicio verdadero (conclusión). El juicio aristotélico considera la relación entre dos términos: un sujeto, S, y un predicado, P. Los términos pueden ser tomados en su extensión universal: abarca a todos los posibles individuos, el dominio de discurso, a los cuales pueda referirse el concepto.2 3 O en su extensión particular: cuando sólo se refiere a algunos.4 Los juicios por la extensión en la que es tomado el término sujeto, como criterio de cantidad, pueden ser: UNIVERSALES: Todo S es P5 PARTICULARES: Algunos S son P6 Nota: Los nombres propios tienen extensión universal; pues el uno, como único, equivale a un individuo que siendo único es, por eso, todos los posibles.7 La relación entre los términos puede ser asimismo: AFIRMATIVOS: De unión: S es P. NEGATIVOS: De separación: S no es P.8 El predicado de una afirmación siempre tiene extensión particular, y el predicado de una negación está tomado en su extensión universal. Cuando un concepto, sujeto o predicado, está tomado en toda su extensión se dice que está distribuido; cuando no, se dice que está no distribuido. Según el criterio de cantidad y cualidad, resulta la siguiente clasificación de los juicios: CLASE DENOMINACIÓN ESQUEMA EXPRESIÓN-EJEMPLO Extensión de los términos A Universal Afirmativo Todo S es P Todos los hombres son mortales S: Universal P: Particular E Universal Negativo Todos los S no son P Ningún hombre es mortal S: Universal P: Universal I Particular Afirmativo Algún S es P Algún hombre es mortal S: Particular P: Particular O Particular Negativo Algún S no es P Algún hombre no es mortal S: Particular P: Universal Los juicios se relacionan unos con otros en lo que constituye un argumento. El silogismo argumenta estableciendo la conclusión como una relación entre dos términos, establecida como resultado de la comparación de ambos términos con un tercero (tertium comparationis). Por eso se define: Silogismo es la argumentación en la que a partir de un antecedente, (dos juicios como premisas), que compara dos términos, (sujeto y predicado de la conclusión), con un tercero, (término medio), se infiere o deduce un consecuente, (un juicio como conclusión), que une, (afirma), o separa, (niega), la relación de estos términos, (sujeto y predicado), entre sí. ANTECEDENTE = Dos premisas: Premisa mayor, en la que se encuentra el término mayor, que es el predicado de la conclusión, que se representa como P. Premisa menor, en la que se encuentra el término menor, que es el sujeto de la conclusión, que se representa como S. Entre ambas se realiza la comparación del término sujeto y el término predicado con respecto al término medio, que se representa como M. CONSECUENTE = Una conclusión: En la que se establece la relación entre el término sujeto S, y el término predicado P. TÉRMINOS: Término mayor: Es el predicado de la conclusión. La premisa en la que se encuentra se llama premisa mayor. Se representa como P. Término menor: Es el sujeto de la conclusión. La premisa en la que se encuentra se llama Premisa menor. Se representa como S. Término medio: Que sirve de comparación (tertium comparationis) y no puede estar en la conclusión. Se representa como M. Figuras y modos silogísticos[editar] Teniendo en cuenta la disposición de los términos en las premisas y en la conclusión se pueden dar las siguientes FIGURAS SILOGÍSTICAS, que se denominan: 1ª 2ª 3ª 4ª FIGURA FIGURA FIGURA FIGURA MP PM MP PM SM SM MS MS SP SP SP SP Premisa mayor Premisa menor Conclusión Los modos son las distintas combinaciones que se pueden hacer con los juicios que entran a formar parte de las premisas y la conclusión. Como estos juicios tienen cuatro tipos distintos (A,E,I,O), y en cada caso se toman de tres en tres —dos premisas y una conclusión— hay 64 combinaciones posibles. Estas 64 combinaciones posibles quedan reducidas a 19 modos válidos, al aplicar las reglas del silogismo. Reglas del silogismo[editar] Reglas para los términos[editar] El silogismo no puede tener más de tres términos. Esta ley se limita a cumplir la estructura misma del silogismo: La comparación de dos términos con un tercero. Aunque la regla es clara, su aplicación no siempre lo es. Es lo que algunos llaman silogismo de cuatro patas. Ver quaternio terminorum. Consideremos el siguiente silogismo: Los hombres son esencialmente libres. Las mujeres no son hombres. Las mujeres no son libres. Los términos que aparecen como evidentes son las palabras hombre, libre, mujer. Pero, a modo de un non sequitur en la supuesta premisa mayor se utiliza la palabra hombre en su acepción de especie (Homo sapiens) mientras que en la supuesta premisa menor del quaternio terminorum se ha trocado el significado de la palabra hombre utilizando la acepción de [sexo] (hombre como sinónimo de varón), es decir se ha incluido subrepticiamente un cuarto término, de allí que la conclusión del quaternio terminorum es errónea, un sofisma. Si se observa bien, en el ejemplo dado de quaternio terminorum se ha expresado de un modo entimemático. Los términos no deben tener mayor extensión en la conclusión que en las premisas. Por la misma estructura del silogismo; únicamente podremos obtener conclusiones acerca de lo que hemos comparado en las premisas. El término medio no puede entrar en la conclusión. Por la misma estructura del silogismo la función del término medio es servir de intermediario, como término de la comparación. El término medio ha de tomarse en su extensión universal por lo menos en una de las premisas. Para que la comparación sea tal, es necesario que el término medio sea comparado en su totalidad. De otra forma, podría ser comparado un término con una parte y el otro con la otra, constituyéndose en realidad entonces un silogismo de cuatro términos. Todos los andaluces son españoles. Algunos españoles son gallegos. Por tanto, algunos gallegos son andaluces Lo que evidentemente no es un modo válido, puesto que "españoles" en la premisa mayor al ser predicado de una afirmativa está tomado en su extensión particular. Reglas de las premisas[editar] De 2 premisas negativas no puede obtenerse conclusión alguna. Dos premisas negativas no se adaptan a la estructura del silogismo, ya que si negamos S de M, y P de M, no sabemos qué relación puede haber entre S y P. Para establecer la relación, por lo menos uno de los términos tiene que identificarse con M. Por tanto una de las dos premisas tiene que ser afirmativa. De dos premisas afirmativas no puede sacarse una conclusión negativa. En efecto, si S se identifica con M, y P también se identifica con M, no tiene sentido establecer una relación negativa con entre S y P. La conclusión será afirmativa. La conclusión siempre sigue la peor parte. Entendiendo por peor parte, la negativa respecto a la afirmativa y lo particular respecto a lo universal. Veamos los dos casos separadamente: a) Conclusión negativa de una premisa afirmativa y la otra negativa. Si se afirma una relación entre dos términos (X, M), pero se niega la de uno de ellos con otro (Y, M), siendo M el término medio, no puede haber más conclusión que negar la relación que pueda haber entre el primero (X) y el último (Y) siendo uno sujeto y el otro predicado de la conclusión. b) Conclusión particular de una premisa universal y otra particular (teniendo en cuenta que dos premisas particulares no puede ser, como veremos en la regla siguiente). Pueden darse dos casos: Que una sea afirmativa y la otra negativa, o que las dos sean afirmativas. 1º) Dos afirmativas. (Tenemos que recordar que el predicado de una afirmativa está tomado en su extensión particular, y el predicado de una negativa en su extensión universal). Al ser las dos afirmativas sus predicados son particulares. El término de la universal tiene necesariamente que ser el término medio, la conclusión tiene que tener un sujeto particular. 2º) Una afirmativa y otra negativa: Tiene que haber dos términos universales. Uno de ellos tiene que ser el término medio, el otro tiene que ser el predicado de la conclusión, pues la conclusión tendrá que ser negativa, (caso a) de esta misma regla). Por tanto el término que queda será el sujeto de la conclusión con extensión particular. De dos premisas particulares no se saca conclusión. También tiene dos casos posibles: que una sea afirmativa y la otra negativa o que las dos sean afirmativas. a) Afirmativa y negativa: Algún A es B - Algún A no es C. Sólo hay un término universal que es el predicado de la negativa, que por tanto tiene que ser el término medio. La conclusión tendrá que ser negativa (caso a) de la regla anterior), y por tanto el predicado tendrá que ser universal, y no puede ser el término medio por tanto no puede haber conclusión. b) Dos afirmativas: Algún A es B - Algún A es C. Los tres términos son particulares, y por tanto no puede haber término medio con extensión universal, y por tanto no hay conclusión posible. Los modos válidos[editar] Modo del silogismo es la forma que toma éste de acuerdo con la cantidad y la cualidad de las premisas y la conclusión. De la aplicación de las leyes de los silogismos a los 256 modos posibles resultan válidos solamente 19 y son los que tradicionalmente se memorizan atendiendo a los modos válidos de cada figura con sus premisas y conclusión. Así los modos válidos Se memorizaban cantando De la primera figura AAA, EAE, AII, EIO BARBARA, CELARENT, DARII, FERIO De la segunda figura EAE, AEE, EIO, AOO CESARE, CAMESTRES, FESTINO, BAROCO De la tercera figura AAI, IAI, AII, EAO, OAO, EIO DARAPTI, DISAMIS, DATISI, FELAPTON, BOCARDO, FERISON De la cuarta figura AAI, AEE, IAI, EAO, EIO BAMALIP, CAMENES, DIMATIS, FESAPO, FRESISON FIGURAS DEL SILOGISMO Teniendo en cuenta la disposición de los términos en las premisas y en la conclusión se pueden dar las siguientes FIGURAS SILOGÍSTICAS, que se denominan: 1ª 2ª 3ª 4ª FIGURA FIGURA FIGURA FIGURA MP PM MP PM SM SM MS MS SP SP SP SP Premisa mayor Premisa menor Conclusión Los modos son las distintas combinaciones que se pueden hacer con los juicios que entran a formar parte de las premisas y la conclusión. Como estos juicios tienen cuatro tipos distintos (A,E,I,O), y en cada caso se toman de tres en tres —dos premisas y una conclusión— hay 64 combinaciones posibles. Estas 64 combinaciones posibles quedan reducidas a 19 modos válidos, al aplicar las reglas del silogismo. SILOGISMOS ESPECIALES Se llaman silogismos especiales porque no tienen la misma forma del silogismo categórico, que hemos estudiado antes. El Entimema es un silogismo abreviado donde falta una premisa, o la conclusión. El Epiquerema es un silogismo donde las premisas tienen una explicación añadida. El Sorites es un silogismo con más de tres premisas donde su mecánica es que el sujeto y el predicado se van intercalando hasta llegar a la conclusión. En Lógica, Entimema (< latín enthymēma < griego ἐνθύμημα o enthumēma [en + thumos (mente) - 'que ya reside en la mente']) es el nombre que recibe un silogismo en el que se ha suprimido alguna de las premisas o la conclusión, por considerarse obvias o implícitas en el enunciado. Al entimema se le conoce también como Silogismo Truncado. Aristóteles, creador del silogismo, estableció el término y el propio concepto de entimema con dos nociones En (An. Pr., II 27) es un silogismo basado en semejanzas o señales que indican una propiedad que realiza la función de un término medio silogístico. Así pone el ejemplo: “de una mujer que tiene leche se puede inferir que está embarazada”. En otro momento hace referencia a un silogismo incompleto en el sentido de que no se expresa una premisa, que se da por implícitamente sobreentendida. Esta segunda acepción es la que ha pasado a la tradición en los libros de lógica. Todavía hay (William Rowan Hamilton, 1856) quien también lo considera cuando se suprime la conclusión. Ejemplos[editar] He aquí un entimema de primer orden: Como hombre que es, Sócrates es mortal, en el que se ha omitido la premisa mayor: Todos los hombres son mortales. Si se exponen las tres proposiciones del silogismo, quedan: Premisa mayor - Todos los hombres son mortales (omitida). Premisa menor - Sócrates es hombre. Conclusión - Sócrates es mortal. Y como ejemplo de entimema de segundo orden: Todos los hombres son mortales. Por tanto, Sócrates es mortal. En este caso, la premisa omitida es la menor, Sócrates es hombre, luego: Premisa mayor - Todos los hombres son mortales. Premisa menor - Sócrates es hombre (omitida). Conclusión - Sócrates es mortal. LA INDUCCIÒN Método de conocimiento que permite obtener por generalización un enunciado general a partir de enunciados que describen casos particulares. La inducción se considera completa cuando se han observado todos los casos particulares, por lo que la generalización a la que da lugar se considera válida. En la mayoría de los casos, no obstante, es imposible una inducción completa, por lo que el enunciado general a que da lugar la aplicación de dicho método queda sometido a un cierto grado de incertidumbre. En este caso hablamos de inducción incompleta. La inducción incompleta no se puede considerar como un esquema de inferencia formalmente válido, ni se puede justificar empíricamente, por lo que se considera que nos ofrece "verdades" que gozan de un mayor o menor grado de probabilidad, pero que no nos puede garantizar su certeza absoluta. ARGUMENTACIONES SOFISTICAS