Anexo 2
Anuncio
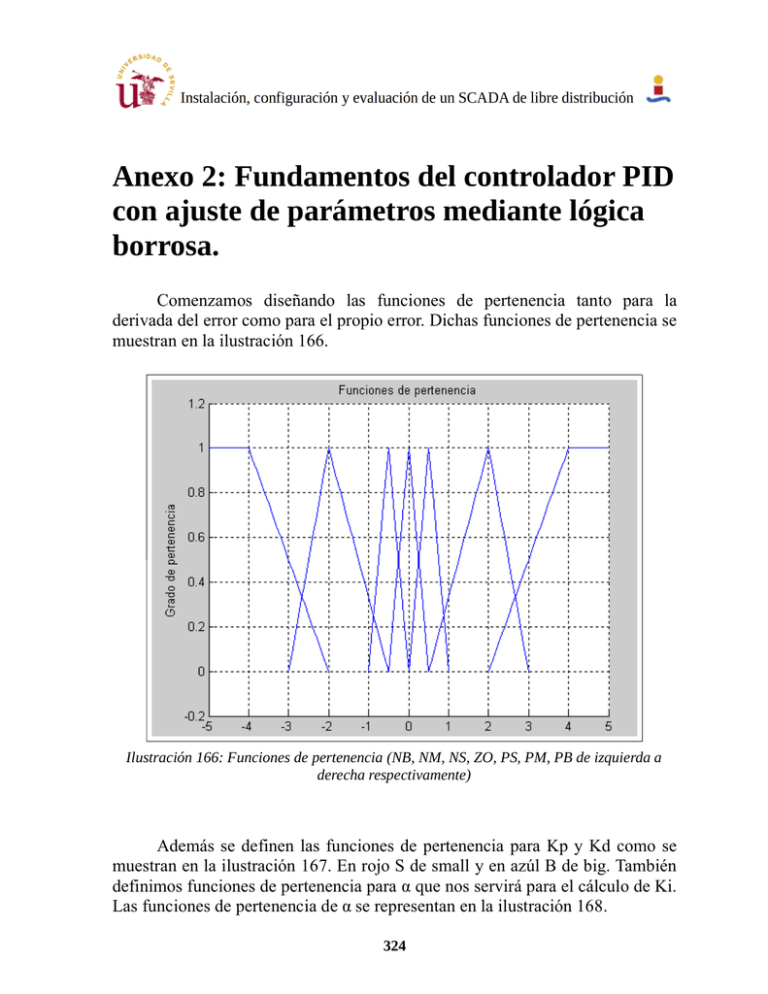
Anexo 2: Fundamentos del controlador PID con ajuste de parámetros mediante lógica borrosa. Comenzamos diseñando las funciones de pertenencia tanto para la derivada del error como para el propio error. Dichas funciones de pertenencia se muestran en la ilustración 166. Ilustración 166: Funciones de pertenencia (NB, NM, NS, ZO, PS, PM, PB de izquierda a derecha respectivamente) Además se definen las funciones de pertenencia para Kp y Kd como se muestran en la ilustración 167. En rojo S de small y en azúl B de big. También definimos funciones de pertenencia para que nos servirá para el cálculo de Ki. Las funciones de pertenencia de se representan en la ilustración 168. 324 Ilustración 167: Funciones de pertenencia (B, S) para Kp y Kd Ilustración 168: Funciones de pertenencia ( S, MS, M, B) para Ahora inferimos las reglas de la típica respuesta ante escalón del sistema, al principio necesitamos una gran señal de control, para lo que necesitamos una gran Kp y una pequeña kd, la ganancia integral es inversamente proporcional a . Así tenemos: IF e(t) is PB and e(t) is ZO, THEN Kp is Big, Kd is Small, is S 325 Utilizando inferencias de este tipo completamos tres sets de 49 reglas para Kp, Kd y , que resumimos en las siguientes tablas. E(t) NB NM NS ZO PS PM PB NB B B B B B B B NM S B B B B B S NS S S B B B S S e(t) ZO S S S B S S S PS S S B B B S S PM S B B B B B S PB B B B B B B B Reglas para Kp e(t) NB NM NS ZO PS PM PB NB S S S S S S S NM B B S S S B B NS B B B S B B B e(t) ZO B B B B B B B PS B B B S B B B PM B B S S S B B PB S S S S S S S Reglas para Kd e(t) NB NM NS ZO PS PM PB NB 2 2 2 2 2 2 2 NM 3 3 2 2 2 3 3 NS 4 3 3 2 3 3 4 e(t) ZO 5 4 3 3 3 4 5 PS 4 3 3 2 3 3 4 PM 3 3 2 2 2 3 3 PB 2 2 2 2 2 2 2 Reglas para α 326 Combinamos las 49 reglas en cada set utilizando las siguientes fórmulas: 49 y lp A e t B e' t l ' K p= l l =1 49 A e t B e' t l l l =1 49 y ld A e t B e ' t l ' Kd= l l =1 49 A e t B e' t l l l =1 49 ∑ yα µ l α (t ) = l =1 49 ∑µ l =1 Al Al (e(t )) µ Bl (e′(t )) ( e(t )) µ B l (e′(t )) Por último basándonos en el conocimiento de Kpmin y Kpmáx, así como Kdmin y Kdmáx obtenemos los valores de Kp, Kd y Ki atendiendo a: K 'p K p min K p= K p max K p min K 'd K d min Kd= K d max K d min Ki = K p2 αK d Obteniendo un controlador que se adapta a cambios en la referencia y a inesperados en el sistema cómo puede ser una válvula abierta o cerrada. 327