TEMA 4 FUNDAMENTOS DE CÁLCULO DE ESTRUCTURAS.
Anuncio

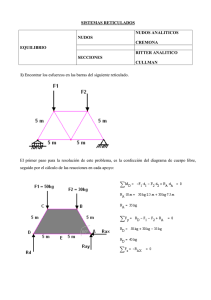
Félix C. Gómez de León Antonio González Carpena TEMA 4 FUNDAMENTOS DE CÁLCULO DE ESTRUCTURAS. Curso de Resistencia de Materiales y cálculo de estructuras. Índice. Introducción. Partes de una estructura. Tipos de Cerchas. Método de los nudos. Método de Ritter. Cremona. Problemas. Partes de una estructura Correas Viga atado Viga Carril 2ª Crujía Cercha 1ª Crujía Ménsula Pilar Cruz de San Andrés Rasante Luz Cimiento Introducción. Si a un triángulo formado por tres barras unidas en tres nudos no alineados le vamos añadiendo barras de dos en dos que se unen en un vértice tendremos una estructura simple articulada e indeformable. Estructura Triangular Canónica: cada triangulo solo esta en contacto con uno anterior y otro posterior (Figura 1). Simple no canónica (Figura 2). Deformable (no simple) (Figura 3). Mecanismo (Figura 4). Isostatismo e hiperestatismo. Una celosía simple, formada a partir de un triangulo, es un cuerpo rígido que tiene tres grados de libertad. Para impedir totalmente su movimiento, se han de disponer tres vínculos que la unan al cimiento. Hiperestática Interna b > 2n-3 Isostática Interna b = 2n-3 (Estrictamente indeformable) Inestable Interna b < 2n-3 Tipología. Jácenas. INGLESA Tipología. Cubiertas. BELGA SWAN POLONCEAU Métodos de los nudos. Se considera sucesivamente cada nudo de la estructura como sólido libre y se aplican las condiciones de equilibrio. Si se toman los nudos en un orden tal, que en ninguno de ellos aparezcan más de dos fuerzas de magnitud y sentido desconocidos pero de dirección conocida, se pueden ir determinando sucesivamente los valores de estas fuerzas, que son los esfuerzos de las barras. Se debe adoptar un sentido de giro para recorrer las barras de cada nudo, comenzando por los conocidos. 4-5 3-4 1-2 5/4P P P 1-2 3-5 3-4 2-4 1-4 NUDO 1 2-3 NUDO 2 2-4 2-3 NUDO 3 1-4 NUDO 4 Método de las Secciones. Método de Ritter. Por este método podemos determinar el esfuerzo en una barra cualquiera sin necesidad de calcular el resto de la estructura, siempre que sea posible dar una sección a la estructura que la divida en dos partes y solo corte a tres barras, una o varias de la cuales son las que pretendemos calcular. El esfuerzo en cada barra se obtiene tomando equilibrio de momentos respecto al punto de intersección de las otras dos. a b A RA c Método de Ritter. Problema. Determinar la fuerza en los elementos FH, GH y GI de la cercha mostrada en la figura. 8m Cremona. 5 P3 = 1'5 kN P2 = 2 kN 4 P1 = 1 kN 3 2 1 7 6 3 R1 4'5 6'5 8 R2 Cremona. Cremona. NUDO 3 P2 N4-5 N2-3 P2 N2-3 N3-6 N3-6 N4-5 Cremona. NUDO 5 N4-5 N7-5 N5-6 N5-6 N7-5 N4-5