4.Localización del vértice

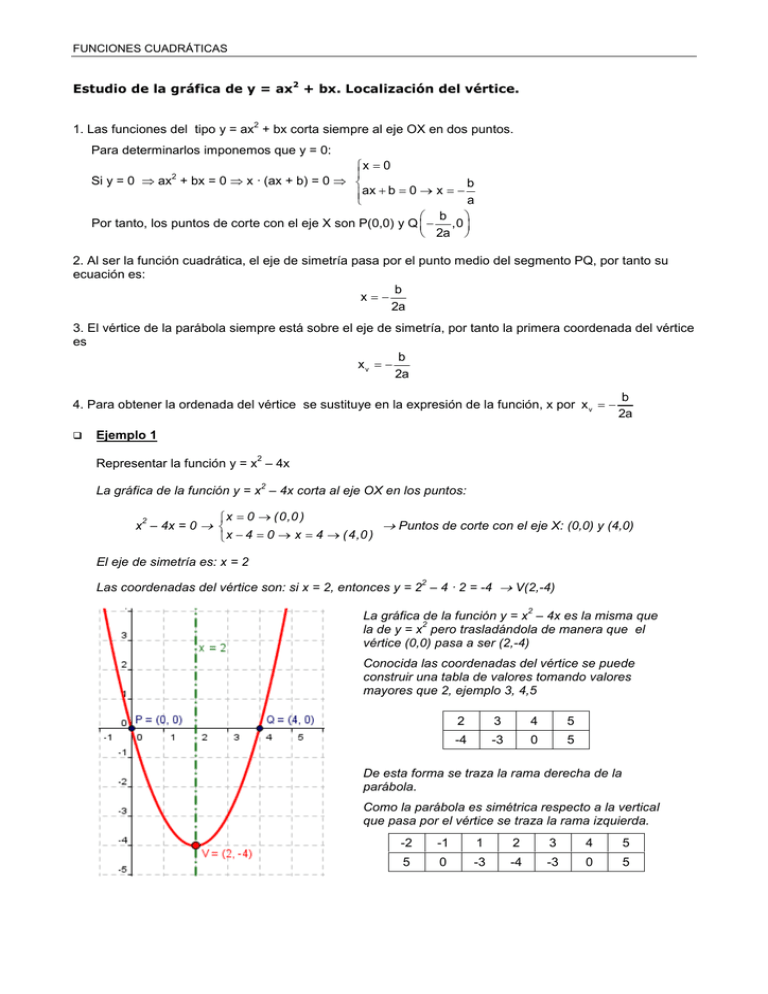
FUNCIONES CUADRÁTICAS
Estudio de la gráfica de y = ax2 + bx. Localización del vértice.
2
1. Las funciones del tipo y = ax + bx corta siempre al eje OX en dos puntos.
Para determinarlos imponemos que y = 0:
x = 0

Si y = 0 ⇒ ax + bx = 0 ⇒ x · (ax + b) = 0 ⇒ 
b
ax + b = 0 → x = − a
 b 
Por tanto, los puntos de corte con el eje X son P(0,0) y Q  − ,0 
 2a 
2
2. Al ser la función cuadrática, el eje de simetría pasa por el punto medio del segmento PQ, por tanto su
ecuación es:
b
x=−
2a
3. El vértice de la parábola siempre está sobre el eje de simetría, por tanto la primera coordenada del vértice
es
b
xv = −
2a
4. Para obtener la ordenada del vértice se sustituye en la expresión de la función, x por x v = −
b
2a
Ejemplo 1
2
Representar la función y = x – 4x
2
La gráfica de la función y = x – 4x corta al eje OX en los puntos:
 x = 0 → (0,0 )
2
x – 4x = 0 → 
→ Puntos de corte con el eje X: (0,0) y (4,0)
 x − 4 = 0 → x = 4 → (4,0 )
El eje de simetría es: x = 2
Las coordenadas del vértice son: si x = 2, entonces y = 2 – 4 · 2 = -4 → V(2,-4)
2
2
La gráfica de la función y = x – 4x es la misma que
2
la de y = x pero trasladándola de manera que el
vértice (0,0) pasa a ser (2,-4)
Conocida las coordenadas del vértice se puede
construir una tabla de valores tomando valores
mayores que 2, ejemplo 3, 4,5
2
3
4
5
-4
-3
0
5
De esta forma se traza la rama derecha de la
parábola.
Como la parábola es simétrica respecto a la vertical
que pasa por el vértice se traza la rama izquierda.
-2
-1
1
2
3
4
5
5
0
-3
-4
-3
0
5
FUNCIONES CUADRÁTICAS
Ejemplo 2
2
Representar la función y = –2x + 6x
2
La gráfica de la función y = –2x + 6x corta al eje OX en los puntos:
 x = 0 → (0,0 )
2
–2x + 6x = 0 → 
→ Puntos de corte con el eje X: (0,0) y (3,0)
 −2 x + 6 = 0 → x = 3 → (3,0 )
El eje de simetría es: x =
3
2
2
Las coordenadas del vértice son: si x =
3
3 9
3 
3 9 
, entonces y = −2 ·   + 6· = → V=  , 
2
2 2
2 
2 2 
2
Teniendo en cuenta la gráfica de y = -2x
2
tenemos representada la parábola y = –2x + 6x
ya que sólo hay que desplazar la primera
3 9 
mediante una traslación de vector  , 
2 2 
Actividad 1
Dibuja la gráfica de las siguientes funciones, determinando las coordenadas del vértice y el eje de simetría:
2
a) y = –2x + 4x
2
b) y = x – 3x
Actividad 2
Determina la expresión de las siguientes parábolas:
2
c) y = 2x + x
2
d) y = –x + 5x