Cap 4: Ejercicios

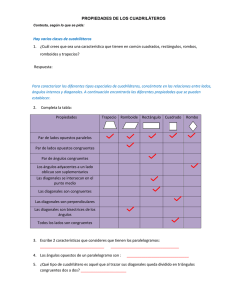
Módulo 17
1. En las siguientes figuras (1 al 9) determine el valor de cada variable.
Figura 1
Figura 2
Figura 3
Figura 4
Figura 5
Figura 6
Capítulo 4: Cuadriláteros
210
Figura 7
2.
Figura 8
Figura 9
En la figura 10:
Hipótesis:
Tesis:
paralelogramo ABCD
M, N, P, Q son puntos medios de
AO , BO , CO y OQ, respectivamente
MMPQ es un paralelogramo.
Figura 10
3.
En la figura 11:
Hipótesis:
Tesis:
ΔABC ; CH ⊥ AB
M punto medio de AC
N punto medio de BC
P punto medio de AB
MNHP es trapecio isósceles
Figura 11
4.
Demuestre que los puntos medios de los lados de un trapecio isósceles son los vértices de un rombo.
5.
Demuestre que el vértice de un triángulo isósceles y los puntos medios de los lados son los vértices de un rombo.
Ejercicios delGeometría
módulo
Euclidiana
17211
212
Auto
Evaluación
Autoevaluación
4
Capítulo 4
Cuadriláteros
Módulos 14 al 17
1.
Determine si cada una de las siguientes afirmaciones es verdadera o falsa.
Si los lados no comunes de los ángulos adyacentes son perpendiculares entre sí, los ángulos son rectos.
Un triángulo isósceles tiene tres ángulos agudos.
Un triángulo isósceles puede ser equiángulo.
Los ángulos alternos son suplementarios.
La medida de un ángulo exterior de un triángulo es igual a la suma de las medidas de dos ángulos interiores.
Un ángulo exterior de un triángulo es por lo menos el suplemento de un ángulo interior del triángulo.
En un triángulo rectángulo en el cual un ángulo agudo mide 30º la medida de la hipotenusa es la mitad de la medida
del cateto opuesto al ángulo de 30º.
La medida del segmento rectilíneo que une los puntos medios de dos lados de un triángulo es igual a la medida
del tercer lado.
Las bisectrices de los ángulos opuestos de un rectángulo son paralelas.
Las bisectrices de los ángulos adyacentes de un paralelogramo son perpendiculares.
Un paralelogramo es equilátero si tiene dos lados congruentes.
Un trapecio es equilátero si tiene dos lados congruentes.
Los lados no paralelos de un trapecio isósceles forman ángulos congruentes con las bases.
Los segmentos que unen los puntos medios de los lados opuestos de un cuadrilátero se cortan en sus puntos
medios.
La mediana de un trapecio biseca a cada diagonal.
Las rectas que pasan por los vértices de un paralelogramo, paralelas a las diagonales, forman otro paralelogramo.
Las rectas que pasan por los vértices de un cuadrilátero, paralelas a las diagonales, forman un paralelogramo.
2.
Determine el(los) cuadrilátero(s) que cumple(n) la propiedad dada.
Los lados opuestos son paralelos.
Los lados son congruentes.
Los lados opuestos son congruentes.
Las diagonales se bisecan.
Las diagonales bisecan los ángulos.
Las diagonales son perpendiculares.
Las diagonales son congruentes.
Los ángulos opuestos son suplementarios.
Los ángulos adyacentes son suplementarios.
3.
Cada una de las siguientes afirmaciones acerca de un cuadrilátero bastaría para demostrar que es paralelogramo
o cuadrado, o rectángulo, o rombo. Escriba al final el nombre del cuadrilátero correspondiente. Si la información
no es suficiente para ninguno de los cuadriláteros mencionados, al final escriba «ninguno».
Geometría Euclidiana 213
Tiene sus lados congruentes _____________________________________________
Tiene dos lados consecutivos congruentes y perpendiculares ____________________
Las diagonales son congruentes __________________________________________
Las diagonales se bisecan ______________________________________________
Las diagonales son perpendiculares y congruentes ____________________________
Cada dos ángulos consecutivos son suplementarios congruentes _________________
Las diagonales son bisectrices de los ángulos correspondientes __________________
Dos lados consecutivos son perpendiculares y congruentes _____________________
Las diagonales son mediatrices entre sí _____________________________________
Una diagonal está contenida en la bisectriz a dos ángulos _______________________
Cada dos ángulos consecutivos (adyacentes) son suplementarios _________________
Dos ángulos consecutivos (adyacentes) son suplementarios _____________________
Una diagonal determina dos triángulos congruentes ____________________________
Cada dos lados consecutivos son perpendiculares _____________________________
Las diagonales son congruentes y mediatrices entre sí __________________________
Dos lados son paralelos y los otros dos son congruentes ________________________
Dos lados son paralelos y dos ángulos opuestos son congruentes _________________
Dos ángulos opuestos son rectos __________________________________________
En cada una de las siguientes figuras (1 a 10) encuentre el valor numérico de la(s) variable(s).
4.
5.
Figura 1
6.
Figura 2
7.
Autoevaluación
Autoevaluación
Figura 3
214
Figura 4
8.
9.
Figura 5
10.
Figura 6
11.
Figura 7
12.
Figura 8
13.
Figura 9
Figura 10
Euclidiana
Geometría Euclidiana
Geometría Euclidiana 215
De acuerdo con la figura (11 a 20) demuestre lo solicitado.
14.
En la figura 11:
Hipótesis:
paralelogramo ABCD
DB, AC diagonales
AC corta a DB en O
N −O − M
Tesis:
ON ≅ OM
Hipótesis:
trapecio ABCD
Tesis:
P y S puntos medios de DA y CB
PS biseca las diagonales
Figura 11
15.
En la figura 12:
Figura 12
16.
En la figura 13:
Hipótesis:
triángulo ABC con AM mediana
l ≅ M BN
l
M CP
Tesis:
CPBN es un paralelogramo
Figura 13
Autoevaluación
Autoevaluación
216
17.
En la figura 14:
Hipótesis:
paralelogramo ABCD
AP = PB, AB = 2AD
Tesis:
PD ⊥ PC
Figura 14
18.
En la figura 15:
Hipótesis:
ΔABC equilátero
O punto interior del ΔABC
ON ⊥ BC , OM ⊥ AB,
OP ⊥ AC , CH ⊥ AB
Tesis:
OM + ON + OP = CH
Hipótesis:
ΔABC rectángulo en C
Figura 15
19.
En la figura 16:
CH ⊥ AB, HP ⊥ AC , HN ⊥ BC
CM mediana
l ≅ Bˆ , C NP
l ≅ Aˆ ,
PN ≅ CH , C PN
Tesis:
CM ⊥ PN
Figura 16
20.
En la figura 17:
Hipótesis:
ΔABC con BQ, AN , CM
medianas
PM ≅ QB , PM & QB
Tesis:
Figura 17
PC ≅ AN
Euclidiana
Geometría Euclidiana
Geometría Euclidiana 217
21.
En la figura 18:
Hipótesis:
paralelogramo ABCD
AQ bisectriz de Â
Tesis:
CP bisectriz de Ĉ
D − A − P; B − C − Q
APCQ es un paralelogramo
PF ≅ EQ
PDQB es un paralelogramo
Figura 18
22.
En la figura 19:
Hipótesis:
cuadrado ABCD
Las diagonales se cortan en O
MN ⊥ PQ ; MN ∩ PQ en O
Tesis:
PMQN es un cuadrado
Hipótesis:
CA = CB; C − D − B
AH = AE; A − K − E − B
HF = HI; H − I − E − D
F −I−K
Figura 19
23.
En la figura 20:
Tesis:
(
)
( )
l
m C DH
= 6m Fˆ
Figura 20
Autoevaluación
Autoevaluación
218
Demuestre las siguientes proposiciones (24 a 36):
24.
Si un triángulo tiene dos alturas congruentes, es isósceles.
25.
Si dos medianas de un triángulo son perpendiculares a los lados, el triángulo es equilátero.
26.
En un triángulo rectángulo la bisectriz del ángulo recto es bisectriz del ángulo entre la altura y la mediana relativas
a la hipotenusa.
27.
En un triángulo rectángulo la mediana y la altura relativas a la hipotenusa forman entre sí un ángulo que tiene como
medida la diferencia de las medidas de los ángulos agudos.
28.
En un triángulo ABC cualquiera, CH es la altura y CD es la bisectriz de Cˆ. Si CA > CB, entonces:
( )
( )
⎛ m Bˆ − m Aˆ ⎞
l =⎜
⎟
m H CD
⎜
⎟
2
⎝
⎠
(
)
29.
La diferencia de las medidas de los ángulos que una bisectriz interior forma con el lado opuesto en un triángulo es
igual a la diferencia de las medidas de los ángulos de la base.
30.
La medida del ángulo formado por la bisectriz y la altura trazadas desde el mismo vértice de un triángulo es igual
a la semidiferencia de las medidas de los ángulos de la base.
31.
En un triángulo rectángulo que tiene un ángulo de medida 30º, la mediana y la altura relativas a la hipotenusa
trisecan el ángulo recto.
32.
Las alturas de un triángulo dividen los ángulos del triángulo en ángulos congruentes dos a dos.
33.
Si dos ángulos opuestos de un cuadrilátero son rectos, entonces las bisectrices de los ángulos opuestos son
paralelas.
34.
Las bisectrices de dos ángulos adyacentes de un paralelogramo son perpendiculares.
35.
En un paralelogramo los segmentos que unen un vértice con el punto medio de los lados opuestos trisecan la
diagonal.
36.
En todo cuadrilátero los segmentos que unen los puntos medios de los lados opuestos y los puntos medios de las
diagonales se cortan en sus puntos medios.
37.
Sean las rectas A 1 y A 2 paralelas. Desde el punto A de una de ellas se baja a la otra recta la perpendicular AC y una
oblicua AB . Luego se traza la secante BED con A − E − L tal que DE = 2BE con A y D en la misma recta. Demuestre
ˆ ) = 1 m ( ABD
ˆ )
que m ( DBC
3
38.
ˆ situado en el exterior del
Un cuadrilátero no convexo ABCD tiene en D un ángulo entrante. Demuestre que ADC
cuadrilátero tiene por medida la suma de las medidas de los ángulos A, B y C.
39.
Se da un triángulo isósceles ABC de base BC. Se prolonga la base BC en una longitud CD = AB, se traza la recta
Euclidiana
Geometría Euclidiana
Geometría Euclidiana 219
AD y se prolonga AB en una longitud BE = BC/2; luego se traza la recta EHF con H punto medio de BC y F en
AD .
(
)
(
)
l = 1 m ABC
l .
a. Pruebe que m ADB
2
b. Pruebe que EA ≅ HD.
c. Pruebe que FA = FD = FH.
(
)
(
)
(
)
ˆ = 62º.
ˆ
ˆ si m BAC
y m ADB
d. Halle m AFH
40.
Las bisectrices de los ángulos opuestos de un paralelogramo al intersecarse forman un rectángulo. ¿Qué cuadrilátero forman si en lugar del paralelogramo se trata de un rectángulo?
41.
ABCD es un paralelogramo y M y N son puntos sobre la diagonal AC tales que A − M − N − C. Demuestre que DMBN
es un paralelogramo si:
a. DM ⊥ AC y BN ⊥ AC.
b. AM ≅ CN .
c. DM y BN son bisectrices.
42.
Por el punto de corte O de diagonales de un paralelogramo ABCD se trazan dos rectas cualesquiera. Una de
ellas corta a AB en E y a CD en F; la otra corta a AD en H y a BC en L. Demuestre que ELFH es un
paralelogramo.
43.
En un paralelogramo ABCD se unen los vértices B y D al punto medio del lado opuesto. Demuestre que AC queda
dividido en tres partes congruentes.
44.
Se unen los puntos medios M y N de las bases AB y CD del trapecio ABCD con los puntos medios P y Q de las
diagonales AC y BD, respectivamente. Demuestre que MPNQ es un paralelogramo.
45.
Sobre los lados de un triángulo ABC se construyen exteriormente los triángulos equiláteros MAB, NBC y PAC.
Demuestre que MC = AN = PB.
46.
Se construye exteriormente al cuadrado ABCD el triángulo equilátero BCP, e interiormente el triángulo equilátero
ABM. Demuestre que los puntos D, M y P son colineales.
47.
Sobre los lados AB y CD de un triángulo equilátero ABC se construyen exteriormente los cuadrados ABDP y
ACMN. Demuestre que la altura AH del triángulo es perpendicular a PN , P N & D M y PC ⊥ BN .
48.
En un triángulo ABC, P es el punto medio de la mediana AM , y MQ & BPN con A − N − Q − C. Demuestre que
NC = 2AN.
49.
Las diagonales del rectángulo ABCD se cortan en O. Por un punto P de AB se traza la recta OP que corta a CD en
Q. Por P y Q se trazan paralelas a la diagonal AC, las cuales cortan a BC en M y a AD en N. Demuestre que
NPMQ es un paralelogramo y que su semiperímetro es igual a la medida de la diagonal del rectángulo.
Autoevaluación
Autoevaluación
220
50.
ˆ ) > m ( AMC
ˆ )y
ABC es un triángulo cualquiera con AB > AC. Se traza la mediana AM. Demuestre que m ( BMA
ˆ ) > m (CAM
ˆ ).
m (CAM
51.
En un triángulo ABC, AM, BN y CP son las medianas. Demuestre que si BC > CA > AB, entonces CP > BM > AM.
52.
Se da un triángulo equilátero ABC de lado A y se prolonga BC una longitud CM = A.
Calcule las medidas de los ángulos del triángulo ACM. Muestre que AM ⊥ AB .
Se prolongan del mismo modo CA = AN = A y AB = BP = A . Pruebe que el triángulo PMN es equilátero.
(Considere el ortocentro O del triángulo ABC.)
Usando el teorema de la paralela media o de la base media, resuelva los ejercicios 53 a 59.
53.
La suma de las distancias de los vértices de un triángulo a una recta cualquiera es igual a la suma de las distancias
de los puntos medios de los lados a esta recta.
54.
La suma de las distancias de los tres vértices de un triángulo a una recta cualquiera es igual a tres veces la distancia
del baricentro a esta recta.
55.
Por uno de los vértices de un paralelogramo se traza una recta cualquiera y de cada uno de los vértices restantes se
traza una perpendicular a la recta. La distancia a la recta del vértice intermedio es igual a la suma o la diferencia de
las distancias a la misma recta de los otros dos vértices (teorema de Varignon).
56.
La suma de las distancias de los vértices de un paralelogramo a una recta exterior es igual a cuatro veces la distancia
del punto de intersección de las diagonales a esta recta.
57.
La suma o diferencia de las distancias de un punto dado a dos lados consecutivos de un rombo es igual a la suma o
diferencia de las distancias a los otros dos lados.
58.
La suma de las distancias de los vértices de un cuadrilátero a una recta cualquiera es igual a cuatro veces la distancia
a esta recta del punto de intersección de las rectas que unen dos a dos los puntos medios de los lados opuestos del
cuadrilátero.
59.
Una recta pasa por el baricentro de un triángulo. La suma de las distancias de dos vértices situados en el mismo
semiplano de borde la recta es igual a la distancia del tercer vértice a dicha recta.
Euclidiana
Geometría Euclidiana
Geometría Euclidiana 221