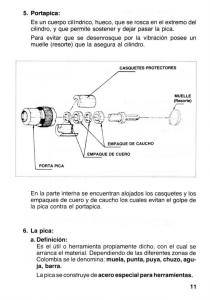
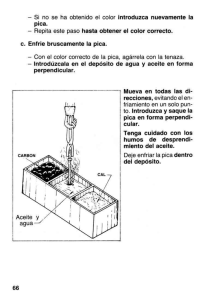
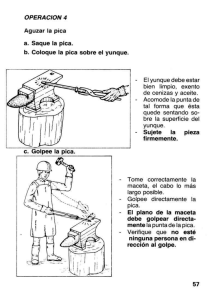
Procedimiento para hacer un gráfico con Excel
Anuncio

Cómo hacer un gráfico con Excel Se confecciona una tabla con los valores medidos en el experimento K0 K |K0-K| F(g) Li (cm) Lf (cm) ΔL(cm) δK 30 15,5 40 16,6 50 17,6 60 12,4 18,8 70 19,6 80 20,6 90 22,8 0 Para calcular el estiramiento se resta a cada valor de longitud final, el valor de la longitud inicial. Se coloca una fórmula fijando el valor de L0 con la tecla F4 y queda de la siguiente manera: K0 K |K0-K| F(g) Li (cm) Lf (cm) ΔL(cm) δK 30 15,5 =C2-$B$5 40 16,6 =C3-$B$5 50 17,6 =C4-$B$5 60 12,4 18,8 =C5-$B$5 70 19,6 =C6-$B$5 80 20,6 =C7-$B$5 90 22,8 =C8-$B$5 0 0 A continuación, se procede a realizar el gráfico de la siguiente manera: Se pica en una celda fuera de la tabla y luego se pica en el icono de asistente para gráficos donde aparece la siguiente tabla. Aparecerá la siguiente pantalla: Se elige el tipo de gráfico XY(Dispersión) y el subtipo que solo marca los puntos como esta en la figura. Luego se presiona siguiente y aparecerá: Se pica en la pestaña “Serie” y luego en “Agregar”. Se pica ahora sobre el icono que se encuentra donde dice “Valores de X” y se seleccionan los valores de la columna ΔL y se presiona “enter”. Luego se pica en el icono que se encuentra donde dice “Valores de Y” y se seleccionan los valores de la columna “F” y se presiona “enter” nuevamente. Se presiona “Siguiente” y aparece esta pantalla: Aquí se completan el título y los nombres y unidades de cada eje, se aprieta “Siguiente” y luego finalizar. Aparecerá el gráfico en pantalla: Ley de Hooke 100 F(g) 80 60 40 20 0 0 2 4 6 8 10 Δ L(cm) Para trazar la recta y obtener el valor más probable de la constante se pica sobre un punto y luego se aprieta el botón derecho del Mouse. Aparecerá esto: Se selecciona “agregar línea de tendencia y entonces quedará: Se selecciona lineal y luego se pica en la pestaña “Opciones”, y se tildan las opciones Señalar intersección” y “Presentar ecuación en el gráfico, queda: Luego “Aceptar” y se obtendrá: Ley de Hooke y = 9,6171x 100 F(g) 80 60 40 20 0 0 2 4 6 10 8 Δ L(cm) En la ecuación puede observarse el valor que toma K0, en este caso: 9,6171≈9,62 Ese valor se agrega en la columna K0 Se calcula cuanto hubiera dado K para cada medición: F(g) 30 40 50 60 70 80 90 0 Li (cm) Lf (cm) 15,5 16,6 17,6 12,4 18,8 19,6 20,6 21,8 ΔL(cm) =C2-$B$5 =C3-$B$5 =C4-$B$5 =C5-$B$5 =C6-$B$5 =C7-$B$5 =C8-$B$5 0 K0 9,62 K =A2/D2 =A3/D3 =A4/D4 =A5/D5 =A6/D6 =A7/D7 =A8/D8 |K0-K| δK Luego se hacen las diferencias entre K0 y cada K particular |K0-K| y se elije el valor más grande, en valor absoluto, como indeterminación : F(g) 30 40 50 60 70 80 90 0 Li (cm) Lf (cm) 15,5 16,6 17,6 12,4 18,8 19,6 20,6 21,8 ΔL(cm) =C2-$B$5 =C3-$B$5 =C4-$B$5 =C5-$B$5 =C6-$B$5 =C7-$B$5 =C8-$B$5 0 K0 9,62 K =A2/D2 =A3/D3 =A4/D4 =A5/D5 =A6/D6 =A7/D7 =A8/D8 |K0-K| =$E$5-F2 =$E$5-F3 =$E$5-F4 =$E$5-F5 =$E$5-F6 =$E$5-F7 =$E$5-F8 δK 0,24