Estudio del triángulo
Anuncio

!
!
"
!
#$
" %
(*
&
&
' *+,'
! "
' (
)
#
* &
*
'+,*
* . /' 0
'+,* +1' , *0 ) +1' , '+,*
'
' +, **'+ ,0
,'
'+,* / * 0 '0 * *0
0 2,
/ * 0
)* *
)
'
'+,* 0
' 0 , *0 +, *
,'
0
,'
'+,* '
0 , '+,* +,0
0
" (
,' '+,*
,
0
'
) '
* +, '
-
'+,*
)
0
/
' '*
*
'+,*
'
, *0 0 +, *
(
0
(
0 *0
*'+ ,0- ' '
,' '+,*
0
3! 4
'+,* ∆
0
)∆
7
'+ , '
−−
≠
6
-(
0
'+ , '
56
*(
0
7 '
5
−−
5
/
*2,
)6 5 6-
(
%
∆
) ' '
-
−−
5
0 0, - (
' - ,( '+
∆
*
−−
- (
5
- 6 5 6 )6 5 6 - ' '
0, /' *
8 (*-
−−
-∆
)∆
) *
−−
*(
2, ' ∆
−− 6 6 6 6
- 5 ) 5
−− −−
5
−−
5
9
'
6
*
'
0
' +, *
*(
0
−−
* + '
6
' '
: 6 ;,'
' +, *
'+,*
(*
−−
,
' +, *
' 0
(
, 0 - ) *, +
−−
'
) - ' '
3! !4- ∆
)∆
'+ , '
'+,*
∆
−−
−−
*(
−−
−−
2,
,( '+
7
& . '
−−
−−
5
56
6 56-
−−
/' !, +
5
−−
)(
−−
-
'+,* +, *
∆
0
656
)∆
'+ , '
(
(* '0 * +,'0
-
' '0 ' , '
- 2, ∆
', &
0
2,
5∆
'
' '
*
'+ , '
−−
-
5
656
'+,* ∆
)
,* ∆
5
7 ' ,'
∆
7
0 '
∆
'+,* /
,'
* *
0 '
'+,* /
* 0
−−
( '0 '
#5∆
#
6 ) #
6
#
0 * '+,*
#6
−− −−
5 #6 -
'
*
−−
#5# -
' '
' 0)
* &
5
<) *,
)
−−
# *(,'
) 6 5 6 - 0 *(
−−
0
- #
+, * -
' '+,*
& . '
−−
0 0 *
-0
0
<0 * '+,* 6
*
' '
#
−−
0 2,
'+ , '
0
#
*
0 0, 2,
-
( ( '0 ,*
*
'+,*
−−
*,
) #
3!!!4
'+,* ∆
0
+, *
)∆
7
(
-(
*(,'
6
56 -
0
'+ , '
- *2,
*(
/ * ) ' '*
0 %
'+,* * &
'+,* % )0
7 '∆
−−
' *
∆
*
' '
)
−−
0
*
'
;
(
-
' 0
6
(
'+,* >
8 (* *
6
'+,* >
0) '
' '
6 ? 6 5 @AB)
6 ? 6 ? 6 5 @AB0 0, 2, 6 5 6 ? 6
−−
- ' '
6≠ 6
,( '+
'
−−
5
(
−−
*
' *
)
5
−−
'+,*
−−
5
'
∆
−−
'
(*'
−−
5
−−
)∆
−−
0 0
!
+ '
)
'
' *, 0 *
'+,*
' ' *
* ' - 6 5 6 ) (* '0 *(
( **
,&
'
'
,& <* +, ' 7
'+,*- , *2,
5
−−
*(,'
- )(
−−
(*' 2,
5∆
−−
5
0 ,'
'+,*
,' '+,* 0) '
,' 0 *
'+,* >
- 2, ' (,
( *&=
' & <&
*
0
+, * ,' **' - 0 * 2,
7 '
-
, 0 - 2, 6 5 6
0, /' *
0 ( ( '0 ,*
2, ( ' (
'+ , ' 3! !4 ,* ∆
5∆
'
−−
5
,'
+, * * ,
'+,* 0 *
2, * ,
0 * 0
'+,*
0 *
'+,* '
'
'
0 '
)
0
0 &=
'+,* 0 ,'
'
0
'
0)
0*
'+,*
'
7
0)
' ,'
'+,*- , *
2,
'+,* >
) 2,
, *2,
0 * 0
'+,*
'
'
'
'
'+,*-
) *0
7 '∆
,( '+
2,
−−
:6 )
96
∆
/
*-
6
6
0
(
(
0
7
' - ,( '+
6 96
0
,*
/'-
6
5
0 0 *0 0 ,'
∆
' 0
−−
96
?
9
)
−−
6
'+,*- )
*(,'
6
5
(
−−
0
−−
*2,
6
0
'
5
−−
0 ∆
'+,* >
) ' '
' - 6 96
! ,
−−
('
−−
-0
.,
−−
6 :6
' '
'+,*
)&
0 2,
(* '0 *
−−
5
2,
65 6
6 96
-
−−
:
∆
' '
∆
'
−−
-
−−
−−
−−
:
−−
9
−−
- (* '0 * (
−−
*0
?
−−
/
,*
.,
* (, 0
) 2, *
(
−−
5
9
,' (,'
* ) 6
−−
-
0
0 *
56
-
−−
*2,
6
?
−−
9
9 6 - ' '
−−
' ( *
*
' * 2,
0
' , ,' .+, + =
, '0
* ' * +* '
+ 0, 0 ) *
( !
*
, /' 0 *( *
'
'
'
' * ' , /' 0 * .+,
' >(*
*
0 0
*< * ) ' . , * 0
/'
( '0 '
*( *
' 0
,*
% C *0 *
= 0 0 ' , /' 0 * .+, ) % 0
0 2,
*< '0 * (
'0 0
' . & ' *
.+,
' * ( ( 0 0 ( 00
! +*
' , ' 0 ' , ' + =
(
<
,'
,*
2, ,'
,*
2, 2, ( ( ,' (,' )
,'
2, ( ( 0 (,' 0 0
' * +* '
(, 0
*< ' '+,'
(
/'7 '
(, 0 ' ' ,
+ ' - ' (, 0 ' , *<
,* '
'
0 0 * +*' *
( (0
0
0 0 ,' '
*
,'. '
0 0 00 ' (
,* - *
( (
' , * + ' +, * ,' + ' 0 0 - ' ,'
00 ) (
0 ,' (,' 0 0
!""#$ %&! &'(&
' ,'
' ,' >
, 0*
+, *
−−
+ '
−−
" ' !& &)!
),'
' ) ,) *'+ ,0
( (' % ' )
' '
−−
* + '
'
%)%
+ ' ' ,' (,'
−−
*0
0 ,8 *
,
0
' *
(
0 *
)
2,
0 ,8 ,'
+ '
(' % ' )
%
'*
,'. '
*
0
-
# ' ' '0 *
'
) 0
D
!""#$ %&! * '!+ " ' !& &)! %)%
0 ,' '+,* 6 - ,'
),'
(*' α 0
' 0 ( *
- 2,
' , ,' '+,*
6
' &=
- ,' *0 *
- ' 00 +, *
) ' '0 'α
' '
'
0 ,8 ,'
,'. ' - 2,
* *0 0 6 ' (,'
) # ' ' '0 *
,
0*
(
0 ,8 ,' 0 ,8 ,'
,'. '
' '
'
) ' *
0 2, * '
,'. '
' ,' (,' E
(' % *
( ' )
%
'
00 - 0 ,8 ,'
,'. '
' '
'E
,'. '
*
,'. '
'
' 0 (,'
' 0
(,'
6
' *
(*' α )* *
*
E ' '
E E
* '+,* , 0
' .
-
−−
−− −−
E6
E E 5 6
' '
5
!""#$ %&+,!
0 ,'
0
−−
E
' .
' '
+ '
−−
5 E )
5 6
−−
−−
5 E E - 0 0 '0 - (
*
2,
- )*, + *
'
,'. '
* 0 <0
-*0 '
0
'* 0
−−
,
'
*(,'
'
0 # )*
'
) 0
<
−−
+ '
−−
/' 0 E '
+, * * 0 '
0
*
0 - & 2, E
*
-∆
5 ∆E
0 ,8 *
,'. '
'
'
' ' 0 (,'
*(,'
0 #
- (, * 0
,'. '
'* 0 <
'
)
)E !
' ' *
0
E
- E)
-
2,
'
, ,'
(' % ' * ( ' )
(' % ' * ( ' )
,'. '
' ' 0 (,'
8
%
'+,* ∆
E
%
*
*
*2, -
'
'
,
,
,' 0 *
*
−−
−−
5 E)
−−
5
−−
,( ' 2,
< ,'
,'. '
' '
< ,'
,'. '
' '
'
' '
∆
* '+,* , 0
& , /+&() "+* #
"
!
, -*
E )
#* '!+ %&+)% %)% 0& #
& % & "!& )&+ & !+)% &+) #
1 )"#"! 2& & "#) 3
−− −− −−
−−
E?
9
'
!, +
<
,'. '
−−
)* '
0
−−
!""#$ %&+
)/#&" #
.%&! * '!+
0 ,' '+,* 6 - <
,'
,'. '
0 '
- 2,
* *0 0 * '+,* '
(,'
) E( & '
' *
, 0* (
0 ,8 ,'
,'. '
'
'
'
)
' '
' E
0
,'. '
' ' ,' (,'
!
*
<0 * '+,*
08
8
0
2,
0
'+ , '
(&%# -%&+)(&%#) #.%&! &'(&
−−
!""#$ %&!
0
+ +
'
' (
( *
/' 0 * '+,* )* , 0 , 0 * ,*
0
'
,
'
+
=
7 * 0,(*
/' 0 *
! 0,(* /' 0 * ,
*( *
'
' *,* **0 0 ,' , 2, ,& 0 * & *, ' 2,
00 ( &
'
**0 2,
,
0
'0 (
0 *(
&
0 ' * +* ) *
(
, ' * 0 /' 2, ,' (0
*/
' %
*D @
' **
' ,*/ *
,* 0 ( *- ' * - ) *
,* ( '0/ 2, 0 ' 0,(*
*& *, ' 0 * * 0
( *- 2, ' .
0 , !
' '
0,(* ' * 0 ' ' 0 * * ) ' '
*& *, '
,* (* / ( @
' - * (0
' 0 (
/ F
+/
.
' *, '
(
* ) ( > 0 0 *( *
2, - ' 0,0 - ' ,) ' * 0
** 0 *
,& ' 2, (
,%
+* ( ( 0 (
2, *( * '
'
*
, /' ' *
.
' 2, * (*'
'* + +
' . - , *< '0
0' 0
'
*( *
0,
G
*& * , /'
' ,
' +* )
5 - ) (, 0 0
2, - (
( ,' + ' 0 *'+ ,0
'0 0 ,' + '
3
- H I4
0 *'+ ,0 - '
(, 0
!
/' 0 * '+,*
( '0 0&0 ,' '+,* '
'+,* +, * - , '0 * * +* ) *
(
'
( * ' + ' *)&
' 0,8 ' , & ,>*
2, *
& '
0 ),0 ( 8 (*- *
0 J(
*
.' =
K ' < *3 @ DL @D@4
0
/2, ,' '+,* α
* ' +* )
(
*( *'
D> M >M
3α4
0, *
!
, 0 , 0 * ,*
( '0
* + + 2, 0 ,8'0 - /*
, ,' , 0 0 0
+, * * 0 ,'
,* 0 0
( *
0
&
.
' *, '
( ' - & * )
00
' ,' + ' (
0 , &0
' '
*&
*( *
3&0 '
'
' ' +, *4 !
(
*0 0 0 * , 0 , 0 *
! '0 '' .' * 0 * +* N N- *%
0
0 * ' '0 '
<0 ' '+,'
, /' *
+
'
. '
'
'
!""#$ %&, +4
'
' +* )
( -'
(,0
( ,(/ , % + '
'
' ' 0 J,
2,
0 * ,0 , 0*
,*
,* ., (*'
' (
0 (
0 *'1
π;
- π ' (, 0
&'!+) &
J)
'
( ' ( * 0 (*'
* ' , /' 0 ( *+ '
+,*
' +* )
( 7
' , *( *+ '
+,* 0 ' *0 2, '
*0 ,' + ' 0 0 ' , *( *+ '
+,* 0 ' *0 ' ( ' ,'
,'. ' 0 0 ' , *( *+ '
+,* 0 ' *0
,'
,'
,'. ' 0 0
! ( *
)
' 2,& *'
0&0 *
,'. '
''(
+, *
!
' , /' 0 ,'
'+,* 2,*
3' 5 4 0 ,' , 0 0 3' 5 D4 (, 0
*< ' , *2,
0 *
='
(, 0 0&0 *
,'. '
'G(
+, * )
' , *( ' + ' ' ( ,'2, * ' , /'
(* 0 2, * '
O
G M O 5 OG='
' *
( *+ '
+,* 0 G *0
(, 0 0&0 *
,'. '
''(
+, * (, 0
,' '+,*(, 0 0&0 *
,'. '
' ' (
+, *
(* '0
*
'
0 0, 2,
(, 0 ' ' ,
( *+ '
+,* 0 7
- H- - DD- @- H- G- A- A- DAG- A- HA- A0
'
( 0 , *0 - ( %, 2, (
,'
AAA C ( 2,
, 3 IIIL @GG4
*< * ' , /' 0 *( *+ '
+,* 0 I *0
P2,= ,
' * ( *+ '
+,* 0 I- Q- - D- Q- *0 R , 0
/
=' 2, * ( * 0&0 *
,'. '
' +* )
( ' ,' '1
(
0 (
+, * '1
,' (
0 S
0 - ,' '1
(
0 *
.
?
3
0 2, '
* ' -*
0 I- Q-
0 * '1
0 *.
G
(
? 5 D QDQHI QI- '
(
4
-
- D- Q?
'(
-
-
*0 '(
'
(
0 S
*
- G- I- GI- HGG I-
H
7
5
, 2, 7 4 *( **+
4 ' ,' ( **+
* *0
,
2, '
, 2,
PE,= * /'
(,
0 ( **+
,' , 0 *
'
','
0
,' , 0 *
' +, *
'& > - 4*
* 0 +' *
'+,*
' ' *(,'
'& >
'
0 ( 0 *0
' *
* 0 '
4R
(,
(,
0 ,' ( **+
' +, * -
0 0
+, * - ' '
6 , 2,
4* , 0 * '+,* '
0 ,' , 0 *
'& >
HA
4* ,
' + 0 0 * '+,* '
0 ,' ( *+ '
'& > 0 ' *0
,' ( **+
@A3' L 4
' '0
'+,*
) T T T * 2,
≡ T T≡ T T- ≡ T )
9
E,
(
2, - '
'0 ' - *
'+,*
) T T T ' '+ , '
' ', /' 0 ,' 2,
0 0
/' ) 1
% 0
(* *
L
* '+,*
) T ' '+ , ' - ' '
*
'+,*
) T T T ' '+ , '
( 2,
7
LF
0
2, * '+,*
) T
''
'+ , ' ,( '+
2,
) T'
' '+ , ' - (,0 '0 0
,' (,' 0 * + '
*2,
≡ T
'
( 2,
' 2,
9 ) T 9 T (,
2,
' (
*
8 P ,'
'
2,
'+,*
7
) T T T
0 0, 2,
+,0 ( 2,
/ * ) 2,
,( ' 2,
)
, '*
< ' '0 (
2,
9 T
' '
2,
>
'
'
T '
) T
'
+ *
'+ , '
0 ,' ( ' + '
'+,* * &
%
*
*+ 0
,'
*
'
'+ , '
' +,0 ) 2,
0
'
)(
'& > R P" 0 ,' ( *+ '
'
'& > 0 ' *0 R
9
,'
'+,*- ) # *(,'
0 0 **0
*
( **
2, ( ( #- 0 ,
2, 7
4
**0
' ,(,'
0
4
*(,'
0 0
5 #
* + '
#
*'
0 ( ** 0 0 * '+,*
* '
0 0, 2,
( 2, ,'
* (,'
0 0 0 *0 0 ,'
'+,*- * + '
,* '
( ** *
*0
:
' ,'
'+,* ,'
* (,'
0
0 , *0
'
,
;
,'
'+,*- ) #- ) * (,'
0
0 * *0
(,' 0
0 *
0 '
#)
3 %
(
0 2, 0
0 '
8
L4
,
2, 7
4
#5
3
='
5
4
4
T
*(,' 0
0 *
0 '
#)
- P2,= * /' >
0, 2, * (,'
) T ' 0'
'+,* +, * U, . *
)
0 ,'
'
*
( & '
'+,* '
+ '
*
'
T# )
L&
T R
I
De lo anterior se deduce que las tres medianas de un triángulo se cortan en un único punto,
que recibe el nombre de baricentro.
<
,'
'+,*
0 ,' 0 * &=
0 * '+,*
< ,' ( ** **0
.
'0
,' ', &
'+,* T T T
4
,
*
2, ' ' ,' *, 0
- ' '
0 <0 T T T
4
2, *
0
0 ,'
'+,*
' ' ,' (,'
'0
) 4- 0 0, 2, *
' ' ' * *, 0 ,'
'+,*
' ' ,' 1' (,'
*(,' 0
0 *
2, ' ' ' * *,
** ortocentro
' ( *+ '
'& >
0 2,
'
' ,'
,'. '
0 %
,'. '
'
0 2, *
,'. '
,'
4
,
2, ,'
'+,* , *2,
(
(, 0 '
,'
4
4 ' ,) ,' , 0 *
'& > 2, ' (, 0
'
' ' '+,'
6
4
4
4
, 2, ' , *
2,
0 *
(
00 * '+,* ' *
( '0 '
'
'+,*
) T T T 0
) T T T '
≡ T T ) 6 ≡ 6T
≡ T T)
≡ T T
6
≡ T T ) ≡ 6T
'
'+,*
'+ , '
(
2,
,'. '
* 2, '0 ' * .+,
'+,*
' '+,*
& . ,' , *
2,
-
0 ,' 0 , &=
(,' 0
,'
*( *+ '
' ,'
,'. '
3 ,'. '
4
,
2, ' ,' ( *+ '
+,* *
0
0 0 , *0
' ' ,' 1'
(,' - 2, 2,0 0 0 * &=
0 *( *+ '
+,* - **
' 0 *( *+ '
4 0, 2,
(
( *
,'
,'
,'. '
,' ( *+ '
+,*
*
(,
+, '
(,'
%
- * '+,* '
6 ) 6T
( & '
0 * +, ' (
0 '0
,
' 7
2, *
7
' 0 ,' '+,* '& > ' &=
,
2, 7
4
,' (,' 0 *
<0 0 % '+,*- ' '
* 0 '
0
*
2, ' ' ' * *0 0 *
'+,* ' +, *
(
' - E
,' (,' 2, 2,0 0 * *0 0 * '+,* - ' '
E
'*
<0 0 % '+,*
Esto se expresa diciendo que la bisectriz de un ángulo convexo es el lugar geométrico de los puntos
que equidistan de los lados del ángulo.
4
,
2, 0
0 ,'
'+,*
' ' ,' (,'
4
,
2, *
0 ,'
'+,* ' ' , '
El punto de corte de las tres bisectrices
recibe el nombre de incentro.
,' ( ' + '
8
9 '0
* (
2, % )2,
+,*
+, (
,
'
2, *
'+,*
/
,
+* )
( ,' % > + '
'
*
+,*
@
0 ,'
:
,'. '
-
'
,
'
+* )
( ,'
'+,* 2,*
,'
*
,'. '
;
,' (,' >
,'
4
,
2, 0 0 ' > '
*,
0 *
*'+ ,0
4
λ*0 ' 0
3 0 - 03 - 45 λ4 P 2,= , *
2,
*,
<0 0 0
2, λR
* , 0 *'+ ,00- P > 0 0
* , ' *'+ ,00R
4 E ∈ - ) E ,'
,' , 0 *
'& > , *2, - ) # ,
2, # E ,' ( **+
<
(
&
'
,' ( **+
) ) S * (,'
) S 0&0 ' * 0 + ' *
'
+ '
0 * +, ' .+, - 0 '0 *
00 * '+,* ' *
( '0 ' 3(,'
*
' *0 ,8 0 ,'
,'. '
' +* )
6
*
+ '
,'
,'. '
( R
- - ) E * (,'
0
+ '
0
)
(
0
-
&
-
'
)
,
2, *
,'. '
'0 0 * '
'+,*- ) # )
*
0 '
* &
* *0
#)
' '+ , '
' '
* '+,*
/
-0
2, * '+,*
P/
)
* 0
(, 0 0
(
&
'
'
**
0 ( ( *% '0
* # - 2,
( **
' 0
'
)
'
)
- )( ( * (,'
*+ '0 0 0 - **&
# )
%>+ '
( & ' F .+,
D
' ,'
&=
2, &
**
'
* (,'
(0
(
0
,
% 0 (* + 0 * + '
(
- E ) - 2, & '
&=
0 0 ,' 0 * .
*
* '
7 4 , 0 * 0 .' /' 0 ( *+ '
+,* ) , '
* , 0 * '+,* '
0 ,' ( *+ '
0, * 2, % 0
0 0 '+,* '
0 ,' % > + '
+,*
4 +, * ( ,
+, '
' * 8 & 0 ' ,
0 ' (*+ 0 0 ( ( *,' % > + '
+,*
,'
'+,* 0 ( ( *
8 (* 0 G
0 * + )G
0 ' %
'
,'
** =
)
'+ , '
'+ '
*
0 ' * .+, 4
' *2, '
0
' *'+ ,0
,'
0
2,
'& >
'+,*
+ ' -
)
+, '
) '
7
0*
Q
L
E (*+
( ( '0 ,* '
L *+ 0 0 )%
' 0
G
*
(
( ( '0 ,* '
ET ∈
- T∈
2, 0 ' 0 *
H
2, *% > + '
,* '
' '0 ' , ' * .+, - 0 ,
8
* '
/' 0 * ( ( '0 ,*
<0 )
* '
/' 0 *', & (* +, )
' '0 # 0 ' (*+ 0 0 , 0 - 0
'
2, - E )
( & '
EET T T
- . & ' - +,*
'
2, * '+,*
) /*
0
T∈ # -
0 *
,'. '
9
0 ,' ( *+ '
'& >
0 2,
,'
,'
,'. ' 3 ,'. '
'
4
0
*0
'+ '
*
,'. '
4
,
2, *' ' 0 ,'
'+,*
' 0 ,'
,'. '
'
' *
4 ' ,) ,' , 0 *
'& > ' *2, ' (, 0 '
' '+,'
,'. '
4 , 0 * 0 .' /' 0 ' 0 ,' ( *+ '
+,*
% (
0 2, 0 % (,'
' 0 ,'
,'. '
2,
,'
* ( *+ '
,
2, 0 %
'
='
'
0 ,'
,'. '
'
' *( *+ '
( '0 < ' 0 '
& 00
.* 0 ,' 0 * .
'
+, '
4 ' 0
'+,*
'+,* * %( ',
) 2, , *2, 0 *
4 (, 0 ' , ,'
'+,* 0 *0 0 H- A)
4 (, 0 ' , ,'
'+,* ,) '+,*
'*
00 * 0
04 (, 0 ' , ,'
'+,* ,) *0
'*
00 * 0
.4 ' ,'
(, 0 '
,'
,'. '
+4 '
'+,* ' 2,*
' (, 0
,'
,'
,'. '
%4 ' ,'
'+,* 2,*
* (,'
' ' - ' ' ) ,' '
4
,'
'+,* ' * , ** 0 ' #
=' *, - ' '
84
,'
'+,* ' * , ** *, #
='
<- ' '
:
;
,
,'. '
,
(,
<
*0
!
P, '
&=
2, ' 0
'+,*
'
) ,'
2,
-
(,
0 *
,'
,' , 0 *
'+,*
* '+,*
+, * * 0 * 0
,'
'& >
& *0
'& > '
,'. '
- ' '
0 *
* ,
,'. '
-)
,
2, 7
6
(,'
'
'+ , '
0 A@A - P , '
* '+,* ' *.
' ,'
'+,* 0 '+,*
) '+,*
0 *
02, * %( ',
' ) 0 (,'
0 ,'
0*
(*'
3 4
6 ) 6
4 E∈ - ' '
E
' 0'
/ *
/ *
0 0
0
* '+,* '
0 ,' ( *+ '
' *
0 2, .,
+,* - P , '
' * ' R
2,
'
,'
*
,' , 0 *
+, * * , 0 *
, 0 0
0 +' * R
' ,&
,
' ,(*
'+,*- * ,
7
,'. '
0 A
,' (,'
0
,
0 '
&=
' R0 *,' 0
- ' '
*
2, '
0
)0
'+,*
'0
)
'
E ,'
DA
6 ) 6 '
E
4 E∉ - ' '
* '
6
'-
0 0, 2, 7 V* 1'
*
&
) - * 0*
0 (,'
'
+ '
) R
,) ,'
'+ , '
(,'
0
E 0*
(*' 3 4
0 >
0 arco capaz 0 '+,* 6
*'
7
0 ,'
α )0 >
8
'
,'. '
'+,*
'
)
(* ,0α- P( 0
),' '+,* 0
'
0 ,' *0 - * '+,* (,
6
E
* 2, * '+,*
*2, (
'
, ,'
+, * *
V
%
( <0 '+,* 0
*0 - )* *,
* &
9
' * .+, 40
8
' 2, 7
)
' ( ( '0 ,* ) '+ , '
( ( '0 ,* ) '+ , ' - # )
' ( ( '0 ,*
E )# (,'
,
2, 7 4 # 5 3
?
4O
4
(,'
0 0 E
4 # 5 EO
'8,'
(* ,0
0 % *0
-
E) E
0 0
'
: !
+, '
,
'
' . 0
* .+, 4- ' * 2,
% ' C *0 *
+,' (
0
* '
+, *
4
* (
0
'+,* 2, (
'
'+ , '
4P
,* 0
(
0
'+,* (, 0 (
2, ' '+ , ' R
4 0, 2, * '+,*
)
' '+ , '
P
C0
'0 /' * 0 0 ( *
≡
SR '
' + & - C * *+1' ( 0 * '
2, - 0
.+, ( ( 0 .
2,
'
., ' +, * - ' (
0 0, 0 % '+ , '
; ' * .+, 4
, 2, #- -
6<
'
,) ,'
6
'
,) ,'
2,
0 A°
6
'
6
,)
'
' 2, 7 # (,'
' *' 0 PE,='
(
/
*
'+,*
+* )
'+,*
'
0 0
0 *
'
'& >
,'. '
≡
* 2, ( '
-)
' * (,'
<0
R
)* 0 + ' *
0 * *'+ ,0 0 *
( ,' ( **+
,' , 0 *
(, 0 '
' ,'
≡
*
-
'
2,
('
,' '+,* 0 *
'+,*
0 ,' '+,* )* *0
2, * '+,*
,
2,
- 2,
)
,'
'+,*
' ( ** - )2,
D
66
' ,) ,'
'+,*
0* + '
- 0 '0
67 4
2, '
( '0 ' 3
**2,
.
'4
4 )10
'
**
68
0* (
' *
,
2, *
'
(
'
0 * .+, -
#
'+,*
' ),0 0 * '
69
'
0 * *'+ ,0 0 **0
*' ' 0
0
'+,*- ,'
0 ' , *2,
(, 0 ( *'+ * 0 '
'
0
'+,*
'
'
(
,) ,' ( **+
, ,'
' ( *0
0
/
'
'
+ '
, ,'
-
'+,*
0 ' -
-*
' 2, *
* 2,
0 )
0 0 *0 ) *
'
)# (,'
' O0 *
'
0 '
( '00
0 0
0 '
,
0
0 '
0 * *'+ ,0 0 ,' 0 , *0 )0 , 0 + ' *
' * +, ' .+, - 0
'
* '.
/' 0 0
0
' '+ , '
*
'0 '
C *0 (, 0
(,'
0 '
/' 0
- ( ' '+,'
* &
'+,*
6:
0
)* *'+ ,0
, 0 * *0 2, *
8
'*
'+,*
'
2,
'+,*
(* ,00 * '+,*
,. ' (
C 0 * 2,
'+ , '
0
(
2, *
'+,*
& ' 0 *'
/' 0
+ '
'+ , '
0
D
* .+,
' * 2, *
0 0, * '+ , ' 0 *
'0 '
'+,*
% ) ' 0 ' ,. '
C *0
- C 0 *+,'
2, - 8,'
' * 00 -
(
6;
0 ,' 0 * *0 0 ,' , 0 0
' ,) '
'+,*
'+,* +, * - 0 %( ', +, *
**0 0 * , 0 0 - 2,
* ' * ' & ' V%
0 ' V) V%
., V3
'0 * .+,
0 *
( +' +, ' 4
4 , 2, * '+,* J
'+,*
/ *
4
U *(,' 0
0 *
)
-)
W *(,' 0
0 *
)
,
2, *
( *+ ' W U ,' , 0 0
4 ' ),0 0 * ( 0 '
- 0 0, 2, * (,' J- )
' *' 0
04P ' *' 0 * (,' J- - )SR
7<
0 ,' 0 *
* ' & ' V%
0'
' *' 0 - ' '
*
*0 0 ,' , 0 0
' ,) '
'+,* +, * - 2,
* '
V) V%
., V3
'0 * .+, 4
,
2,
* (,'
J- - ) S
'+,*
'
'+,* PE,= * /' % ) '
* ,* 0 0 * 8
DQ )= R
D
7 Mosaicos ' 0 C .
0 (
'
' 0 .+, + =
3 *
0 42,
, ' *(*'
'
0 8 %,
' *(
,'
J *
0
+,* , '0 *
*0
' 0 *
( *+ '
+,* - ) 0
0
*0
, * 2,
'
' ' ' '+1' (,'
'
1'* ' ' ,' &=
,' *0
!*
+,*
2, **
2,
'.
0 ( 0 '
( 0 ( *+ '
+,*
2,
' ' ' '
,' &=
,' *0 ) 0
' 0 &=
'.*,) ' *
( *+ ' ) ' *
0'
*
1*
2,
0
* +, '
* 0 0 0 ,' &=
% ) ( *+ '
+,*
- - - * 0
' ,' 0 '
- - & . 2, ' , *2,
&= ( < '0 (
*( *+ '
' '
* ( *+ '
- ' *
+,' 0 * 0 ( *
'
' L +, *
'
* 0 * +,8 0 *
*8L
' * .+, - ' * &=
)F '.*
,) ' *
( *+ '
' *
0' *
' ', /'
* (
(
.'
0 0
0 0* 8
4 '
)
β
,
2,
'+,* '
-)
4
' *
,) '+,* '
4
*'1
0 ** 2, '
'
0 * ( *
* ' *
+,'
0 ( *+ '
+,*
α>β⇔ ' 9
(
'
'+,* '
0 *
0' ( &
0 ( *+ '
+,*
'+,*
,
2,
0 ')
- ,'
' *, '
*0
)
( &
*'1
+,*
0
) +,* 2,
+ ' *2,
' - ) ' '+,* '
0 *0 0 *( *+ '
( *+ '
+,* 0 - D- - G *0 P >
' QQAOI- H - AAO
I- HG + 0 R
* 0 0 0 ,' &=
0 ,'
0 * 0
: X H- 5 ⇔ 5H ) 3LD4X
(, 0 ' ' ,
' 0 , *0 0 (
(
+,* ' ( *+ '
'
*
& α)
)
,
+,*
*( ' ( - ) *'B
04 ' '0 ' , ' *
' 0
'
'
-0
' - ' .,' /' 0 ) - *
, ' ( * 2, ( - (, 0 ' (*'
, '0
' '
* *(*'
4J <,' ,0 (
' < 0 0 0 ,' 0 *
' 0 ' 04( 0
2, *
* 2, '
'0, '
+,*
+,*
.4PJ ( 00
* *(*'
' 0 ( ' + ' ),' 0 + ' R
+4 ' * ,0
*< 0 %
2, %
'0 0
( *
'.+,
'
* 0 0 0 ,' &= - 0 *
,*
( 0, '
+,* - ),' '
& *0 (
*
(
2, *
+,*
0
, * ' * 0
'.+,
'
'
P ,'
+,*
' R
7
-
' * .+, ,' ( **+
-)
, *0
% ' ' ,0 , 0 0 0 '
( &
) D
0
(
2, * , 0 *
,
'
,
0
0
*
*
+
,
*
+
,
'
(
D
' ) S * (,'
0 0 *
+ '
)
( & ' -)
*(,' 0
0 *
0 +' * 0
,
2, *
'+,*
)
S ' '+ , '
4
,
2, * '+,*
'+,*
/ *
4 PE,=(, 0 0
0 *
'+,*
) D
R 0, 2,
,' , 0 0
D
D
DD
' * (
7
4
,
2, *
+ '
4
0
( ( '0 ,*
'
0
)
( **
( '00
' ( ( '0 ,*
- *
,
2,
*
(*'
( **
'
' +, *
T ) T ( **
perpendiculares que se cruzan7
' ( **
**
1*
,* 0 ' (
0 .'
( ( '0 ,*
' ( ( '0 ,* *
4
'
( ( '0 ,*
*
- ' '
( ( '0 , *
**
='
2,
, *2,
,< '
'
0 '
( **
04 ' recta se dice perpendicular a un plano *
0 ,' 0 *
' ' 0 ' 0 % (*'
' '0 ' , ' , >( '
' * (
2,
0 - ',' 0 '
,* 0 2, '8 ,
)2, * ' ' ( ( '0 ,* 0 0 '
)(*' - '
- ( **
'
- ( **
' (*' '
)(*'
# *(,'
76
.+,
*(,'
& '
(
0 0* + '
0
0 *
4
,
2,
4
,
2, *
4
D4
,
2, *
(
+ '
'
#
'
)
*
'+,*
'+,*
-)
-
# ) #
- ) - E-
*
'+,*
'
*
2,*
'+,*
'
,0
-
# -
#
)
'
2,*
)2,
'+,*
,
'
λ * *'+ ,00 ,'
0 ' 0 * '+,*
)µ * *'+ ,00 ,'
0 ' 0 * '+,* #
3' 0 ,' 0
'+,* 0 *
0 ' -(
2,*
- ' ' +, **'+ ,04
,
2, µ =λ/2
+1' *
#
DG
G4
*
(
'
,'. '
'
0
'
# ) 0 * *'+ ,00 * + '
#
,
2, * (,'
-E)
DH
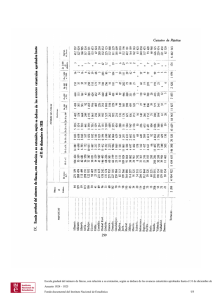
=!&()%& & +!"#$ %&+&>& "#"# %&%&& (# )"#$ %&
*
0
8
,'
' ,'
0
' ,' &=
' , ' 0 ( *+ '
' ' 7 α>β⇔ ' 9
- "!)
# &#
,' ( *+ '
*, '
'
α
HA
D
QA
+,*
G
A@
' *, '
A
I
QAAO
I
+'
*2, &
0 α
@
Q
G
DA
A
DD
+1' *
D
#%&+
H AO
GA
G
G
GH
' 7
&'!+) & 2, % ) * 0 0 0 ,' &= #* '!+ ' 7
< D D D8
E ⇔ E8
+ ... + α = HA ' QAX α : @A( 5 ? - - - 0 0 '0
0 0, 2, QA3L 4? HA X HA- )(
*
)
' 0
*'1
'
'
2, 0 *
*
'
E 8@
E 7@
E 6@
E @
%
D
A@AOI
Q@AO
(
, +4'
' '0 ' , '
' , ' ' ,' &=
* +, ' 7
H
(, 0 ' '
0 ' α1, α2, ..., α L1, α -
&'!+) & ,) '+,* '
α1 + α2 + ... + α L1 + α = HA
HAX α : @A(
0
HA X HA) HA: @A - 0 0 '0 C D8
HA ? α ?
0 63D
0
'
' α )β ( & ' &'!+) @()- & ! * '!+
* +, ' - ' * 2,
#)+&%&% %&! 1A #"&B)- , +4'
'
0 ',
+,* 0 ' ) *0 - ) , '+,* '
()- & &+ ?(& %&+
)% %&+, +
4'
' ' *0 - * '+,* '
H
0
/* % )2, & 2,= ,
'
+'
&
2,
*'1
0 ( *+ '
+,*
2,
'+,* - * #!)"# & , #/+& =!& &,!&%& ,+) &) '
E8
E @6
E <@ @ @
E <@ @
' '
0 ,' 0 *
'
F
,*
'
DI
E 8@ E 8
E 7@ E @6
E 7@ E
'
(
HA? HA? HA? αD ? αG 5 HA ' QAX αD - αG : @A
0 '0
'
'
, /'- 8,'
*
'+,*
' , ' ' *&=
' * +, '
'.+,
' 7
0 0, 2, αD 5 αG 5 QA
0 , 0 0 - (,0='0
E 7@ E 6
'
,
D HA? αG 5 HA
'+,*
,' % > + '
0 '0
' 2, * .+, 2,
' ,
' *&=
8,'
'*
E 6@ E <@ @ @
E 6@ E <
'
'0 ' α ? α ?α ? αD 5 HA ' QAX α : @A(
α 5 QA(
0 ! '.+, /' (,
E 6@ E
5 - - -D
0 '0
' *,) 2,
D@
'0 ' HA ? α ?α ? αD 5 HA ' QA X α : @A (
5 - -D ,
2, α ?α ? αD 5
%) +) 2#'! ) & ) &
"!)% )%
•
α 5 A@
* '+,* ' ' 0 ,' ( ' + '
+,* - α ? αD 5 Q
,
2, QAX α - ' '
QA X α - αD X A - ) ' ' , ' α 5 αD 5 QA
(
& * 0 * '+,* - α ? αD Y Q
** 0 ( '0 2, & +)" 2#'! )"#$
,!&%&& ) ! ,& *'
&'!+
)
•
α 5 A
* '+,* ' ' 0 ,' % > + '
+,* - α ? αD 5 @A ' QAX α : @A(
5 -D
0 '0
' 2, α 5 αD 5 QA- )* +, ' 0
'.+,
'
'
AA-
•
α 9 A
* '+,* ' ' 0 ,' ( *+ '
' '
α ? αD : @A ' QA X α : @A (
5 -D7
(
*0 0
+,*
, /'
' ,' '1
( *
0 *0
) 2, H5 D- 5 - ' (
'
E 6@ E
'
'0 '
HA?α ? αD 5 HA ' QAX α : @A( 5 -D
•
α 5 QA
* '+,* ' ' 0 ,' , 0 0 - αD 5 GA U,'
* 0
'+,*
' , ' ,'
, 0 0 ),' 0 0 + '
•
α 5 A@
* '+,* ' ' 0 ,' ( ' + '
+,* - αD 5
- & * 2, '
( '0 *
00 0 * '+,* ' ' 0 ,' ( *+ '
+,*
•
α 5 A
* '+,* ' ' 0 ,' % > + '
+,* - αD 5 A U,'
* 0
'+,*
' , '
0 %>+ '
+,*
•
* ( ( * 0 α ) αD ' '
*- '*
'
2, 0
(* * ,0
(
5 D- 5
D
E 6@ E
'
'0
' (, 0 0
D
E @ E <@ @
D
E @ E<
'
HA? αD 5 HA ' QAX αD : @A
, /'-
'
0
(
-
DQ
'
α ? α ? α 5 HA ' QAX α : @A ' 5 - 0 '0
0 0, 2, " ( (*F#
(
&+ ?(& %&"!)% )% =!&" "! & & ! 1A #"&& !
•
α 5 QA- α ? α 5 IA ' A@X α : @A ' 5 L
' * '.+, /' (
,' ( ' + '
+,* - *
( *+ '
+,* 0
' ,' '+,*
'
0 H + 0 - 2,
*0 ,' ( *+ '
+,* 0 A*0
' '0 ' , ' ' '
2, ' 0 &=
0*
' , ' ,' ( ' + ' - ,' , 0 0 ),'
/+ '
' *
0'
* - * 0 0 0 ,' ( ' + ' * , /' 2,
+'
* 2,
,
* .+,
,* (,
(
*
L
' * '.+, /' (
,' % ( + '
+,* - *
( *+ '
+,* 0
' ,' '+,*
'
0 QQAOI + 0 - * 2,
( *
(, 0 (
' * * 0 *( ' (
L
' *&=
' , ,' % > + '
+,* - *
( *+ '
,' 0 0 + '
L
' *&=
' , ,' /+ '
+,* - *
( *+ '
/+ '
L
' * '.+, /' (
,' ( *+ ' 0
) '1
0 *0 2, @- *2,
0
'
' '1
0 *0 2, @
)
' 0 0 - * ,0
(* , '0
' * '.+, /' (
,' , 0 0
•
α 5 A@ 3'+,* '
0 (' + '
+,* 4- α ? α 5 G
' A@ X α : @A ' 5 L
' *&=
' ,
(' + '
+,* - *
( *+ ' 0
,' 0 + '
+,*
L
' * '.+, /' (
,' % > + ' - *
( *+ '
'0 2, ' ,' '+,* '
0
+ 0 - ( *
L
' * '.+, /' (
,' ( *+ ' 0
) '1
0 *0 2, H- *2,
0
' ,' '+,*
' 0
+ 0 0 A@
A- (
' * 2, )
'
' (*0
' ' ,'
* ,0
(* , '0 ' *&=
'
' , ' ,0 0 )
*+1' ( ' + '
•
'
' , ' , 0 0 ' ( ' + ' - α ? α ? α 5 HA ' AX α : @A ' 5 - *+ 2, α 5 A(
5 - ! 0 '
'.+,
' 2, (
'(
5 - 5A ' * +, '
GA
D
E @ E
*'1
0
'+,* 2, ' , ' ' ,' &=
,' - α ? α 5 AA
0 α : @A- ")%)
α# %&/& & ()- =!& <
•
,' 0 * α
QAAO
I- *
0
AAOI- 2,
( '0 * '+,* '
0 ,' ( *+ '
+,* 0 D *0 - )* , /' 2,
( 0,
* 2, ,
* .+, +, ' - )2, '0,
,'
'
+,*
•
,' 0 * α
G 3 00 0 '+,* '
'+,* '
0 ,' ( *+ '
+,* 0 D *0 4
0 ,'
!
' * .+,
, /' 2,
( 0,
-
(, 0 (
/+ ' 4- *
'
- ' *+ *
•
,' 0 * α
DD 3 00 0 '+,* '
0 ,' 0 + ' 4- *
'+,* '
0 ,' ( *+ '
+,* 0 G *0 4- ( * , /' 2,
'
'
(
0
, /' .
*
•
'
0 α
(, * 1' (
)
+, *2, GA
*0 02,
( ' (
* , 0
5 - 5 70 00
0
0
( 0,
HG 3 00 0
' *< 0
GH 3 00 0
' *+ *
AA- α 5 GA (
5 + ' ),'
'+,*
G
D
E @ E
'
(*'
' '0 ' , '
•
•
•
, /'-
0 *0
HA? α 5 HA ' QAX α : @A
** '
-
&
0 '0
(
*0 0' (, 0
2, 7
* , %)
+,* ( & ' ' 0 *
'.+,
' 3 L L L L L 4- 3DLDLDLD4)3HLHLH42,
(, 0 '
*
* 0 0 0 ,' &=
!
' , /' 0 *
' (
(
2, 0 ,' 0 *
(
*0 0
& *0 J ) (,
+,*
>
,'
* /' ' * 2, ( < ,' ( *+ '
+,*
' ,' '1
0 *0
)
+, *
* ( +,' 0
( *
* ,' (*'
' 0 ( ' + ' ) ,' 0 + '
' , '
' ,' &= (, 0 ' * ' /' 0
( '0 .
& ' (,
2, 3 ALGLG4 ,' 0 *
' & *0 ' * ,0
*< 0
'
+ 0
(
2, ' 0 * &=
(, 0
' '
*
'.+, /'7
L 0 0 +' 0
V 0 0 V0 ( ' + '
L
(' + '
' ,& 0
' ' ,' 0 + '
L (
' &=
' * 2, ' , '
(' + '
( * ' '
* *(*'
' ,' 0 + ' )0 ( ' + '
( *+ '
+,*
' * 2, (
,' ( ' + ' - ( 0
.
2, ','
*+1' ( *+ '
+,*
,' ( ' + '
•
0 0, 2,
' * ,0
( 0, '
2, *
(
* 1'
'.+, /' '
*
* *(*' ' * 2,
*< 0
%'
'0 0
( *
'.+,
'
* 0 0 0 ,' &=
0 * ,*
+,* 7 3 L L L L L 4- 3DLDLDLD4- 3HLHLH4- ),' '
& *0 (
* 7 3 ALGLG4 (
+,* 0
, * ' * 0
'.+,
'
'
G
,0
'00
&
2, '
(
- ' 2, .' * '
*.
/* .
*
'
+,*
% 0 *
*
'* 0
'.,+,
'
2, '
* '
'