V V V VV
Anuncio
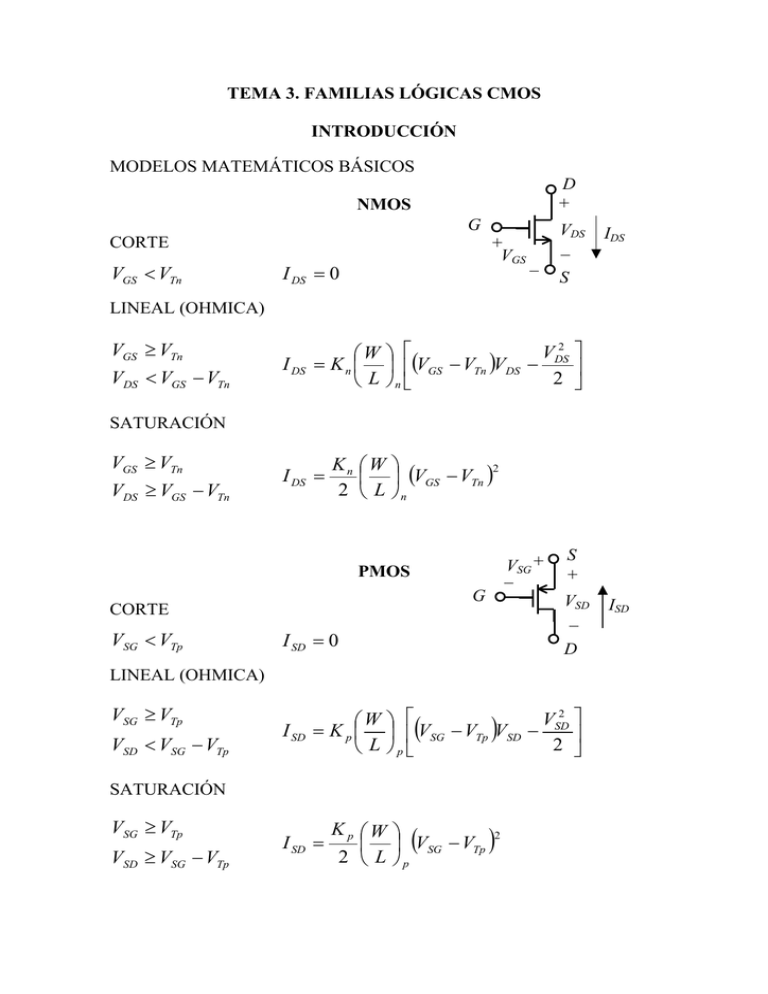
TEMA 3. FAMILIAS LÓGICAS CMOS INTRODUCCIÓN MODELOS MATEMÁTICOS BÁSICOS D + NMOS G CORTE VGS < VTn + VGS _ I DS = 0 VDS _ IDS S LINEAL (OHMICA) VGS ≥ VTn VDS < VGS − VTn I DS 2 º VDS §W · ª = K n ¨ ¸ «(VGS − VTn )VDS − » 2 ¼ © L ¹n ¬ SATURACIÓN VGS ≥ VTn VDS ≥ VGS − VTn I DS = Kn W 2 (VGS − VTn ) 2 L n V + _ SG PMOS G CORTE VSG < VTp I SD = 0 S + VSD _ D LINEAL (OHMICA) VSG ≥ VTp VSD < VSG − VTp I SD 2 º VSD §W · ª = K p ¨ ¸ «(VSG − VTp )VSD − » 2 ¼ © L ¹p ¬ SATURACIÓN VSG ≥ VTp VSD ≥ VSG − VTp I SD = K p W 2 (VSG − VTp ) 2 L p ISD TECNOLOGÍA CMOS Es la más usada, debido sobretodo a su poco consumo y su alta densidad de empaquetamiento. Cualquier circuito CMOS consta de un transistor MOS de canal N y un MOS de canal P, ambos de acumulación o enriquecimiento, que se complementan (Complementary MOS). Ambos transistores deben tener resistencias equivalentes parecidas, esto implica que: VTn ≅ VTp y W W Kn = K p L n L p además, de que ambos transistores tengan la misma tensión de puerta. EL INVERSOR CMOS Es la estructura básica de la tecnología CMOS. VDD MP Vi PULL-UP / LOAD / CARGA Vo MN PULL-DOWN / DRIVER / EXCITADOR CARACTERÍSTICA DE TRANSFERENCIA Para el transistor NMOS VGS = Vi y VDS = Vo Así: si Vi < VTn ⇒ CORTE si Vi ≥ VTn y Vo < Vi - VTn ⇒ LINEAL si Vi ≥ VTn y Vo ≥ Vi - VTn ⇒ SATURACIÓN Para el transistor PMOS VSG = VDD -Vi y VSD = VDD - Vo Así: si VDD -Vi < VTp ⇒ Vi > VDD -VTp ⇒ CORTE si VDD -Vi ≥ VTp ⇒ Vi ≤ VDD -VTp y VDD - Vo < VDD -Vi - VTp ⇒ Vo > Vi +VTp ⇒ LINEAL si VDD -Vi ≥ VTp ⇒ Vi ≤ VDD -VTp y VDD - Vo ≥ VDD -Vi - VTp ⇒ Vo ≤ Vi +VTp ⇒ SATURACIÓN Superponiendo ambas: Vo I II III IV V Vi Transistor NMOS PMOS –VTp VTn VDD –VTp VDD I OFF LIN Región de operación II III SAT SAT LIN SAT IV LIN SAT V LIN OFF PUERTAS LÓGICAS CMOS PUERTA NOR PUERTA NAND VDD VDD F=A⋅B A B F=A+B B A LLAVE DE TRANSMISIÓN C C V(0) [V(1)] C A B A B A B V(1) C V(1) [V(0)] C Estructura Símbolo C Funcionamiento Puerta EX-OR Como las entradas de la llave de transmisión están invertidas si A=0 transmite y si A=1 no se transmite: A B f Si A=0 f=B F = AB + AB = A⊕B Si A=1 f=B A CARACTERÍSTICAS DE LAS FAMILIAS CMOS COMPARACIÓN ENTRE FAMILIAS LÓGICAS