2 kA E =

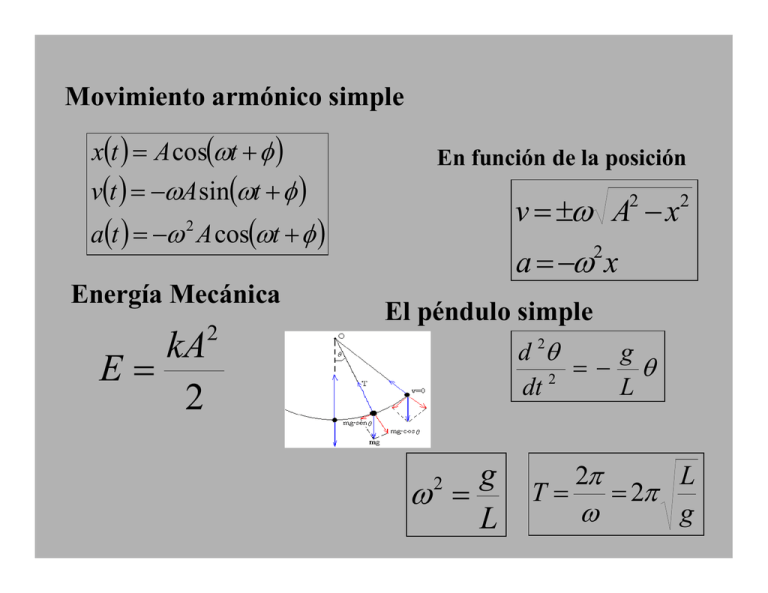
Movimiento armónico simple
x(t ) = A cos(ωt + φ )
v(t ) = −ωA sin(ωt + φ )
En función de la posición
v = ±ω A − x
2
a(t ) = −ω A cos(ωt + φ )
2
Energía Mecánica
kA
E=
2
2
2
a = −ω x
2
El péndulo simple
d 2θ
dt 2
g
ω =
L
2
g
=− θ
L
2π
L
T=
= 2π
g
ω
F (t ) = Fo sin (ωt )
Oscilador Forzado
Fo / m
A= 2
2
ω − ωo
x(t ) = A cos(ωt + θ )
Oscilador Amortiguado
x(t ) = Ae
−
b
t
2m
R = −bv
cos(ωt + θ )
2
b
ω = ω − 
 2m
2
o
Forzado y Amortiguado
A=
Fo / m
(ω −ω )
2 2
2
o
 bω 
+ 
m
2
ω
o
=
k
m
Ondas Mecánicas
Son las ondas que se propagan en los medios
•Fuente de perturbación
•Medio que puede ser perturbado
Tipos de ondas
Transversales
Los elementos del medio se mueven perpendicularmente a
la dirección de propagación de la onda.
Longitudinales
Los elementos del medio se mueven en la dirección de la
propagación de la onda.
El Pulso
y = f (x)
y = f (x − vt)
y(x, t) = f (x − vt)
y(x, t) = f (x + vt)
Función de onda
Representa la coordenada y, de cualquier elemento
situado en la posición x en el tiempo t.
Ejemplos:
I.- Se genero un pulso cuya ecuación de onda es la siguiente
Por comparación con
y(x, t) = f (x − vt)
2
y ( x, t ) =
(x − 3t )2 + 1
v=3 m/s
t=4
t=0
t =1
A=2
t=6
II.- En t=0, un pulso transversal en un alambre está descrito por
la perturbación
6
y= 2
x +3
donde x e y entán en metros. Escriba la función y(x,t) que
describe este pulso si está moviendose en la dirección x positiva
Con una rapidez de 4.50 m/s.
Cambiar
y(x )
por
y ( x − vt )
por lo cual
6
6
y ( x − vt ) =
=
2
2
(x − vt ) + 3 (x − 4.5t ) + 3
III.- Un pulso que se mueve a lo largo del eje x está descrito por
y ( x, t ) = 5.00e
− ( x + 5.00 t )2
donde x es en metros y t en segundos. Determine (a) la
dirección del movimiento de la onda, y (b) la rapidez del pulso
Las ondas de la forma f ( x + vt ) son ondas hacia la izquierda.
Por comparación de
x + vt
con
v = 5.00m / s
x + 5.00t
Pulso
Onda
Ondas senoidales
La onda senoidal es el ejemplo más sencillo de onda
periódica contínua.
sin x
vt
sin( x − vt )
t
t =0
λ
T =
1
T
f =
v =
v
λ
T
= λf
Longitud de onda λ
Es la mínima distancia entre dos puntos idénticos cualesquiera
de ondas adyacentes.
Periodo
Es el tiempo que le toma a la onda recorrer una longitud de onda.
Ejemplo:
Para cierta onda transversal, la distancia entre dos crestas sucesivas
es 1.20 m, y ocho crestas pasan por un punto dado a lo largo de la
dirección de recorrido cada 12.0 s. Calcule la rapidez de la onda.
La distancia entre crestas es la longitud de onda
λ = 1.2m
El periodo es el tiempo que tarda la onda en recorrer una longitud
de onda y al pasar ocho crestas en 12 s esta onda recorre 7
longitudes de onda en 12 s, por tanto
12
T = s = 1.714s
7
Para la velovidad de la onda tenemos
λ
1 .2 m
v= =
= 0 .7 m / s
T 1 .714 s
En general la una función senoidal, tiene la forma
y ( x, t = 0) = A sin (ax + b )