Extremos de funciones de dos variables
Anuncio
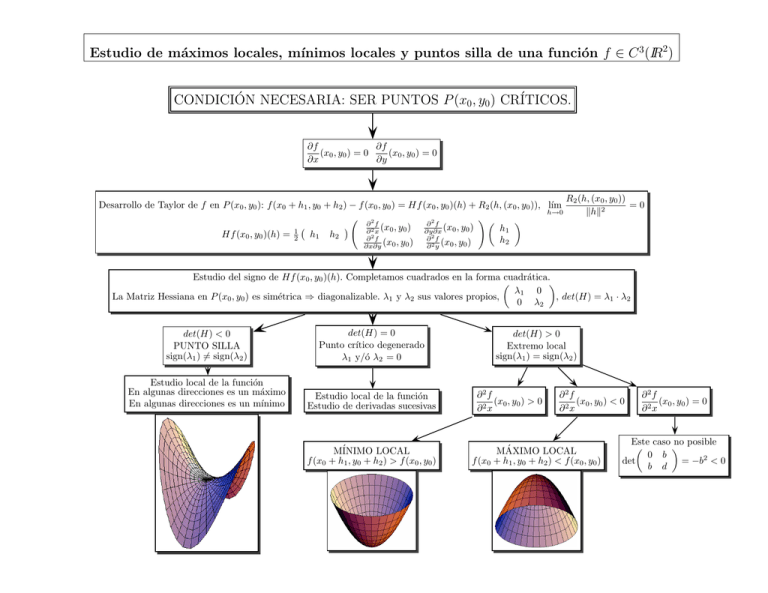
Estudio de máximos locales, mı́nimos locales y puntos silla de una función f ∈ C 3 (IR2 ) CONDICIÓN NECESARIA: SER PUNTOS P (x0 , y0 ) CRÍTICOS. ∂f ∂f (x0 , y0 ) = 0 (x0 , y0 ) = 0 ∂x ∂y Desarrollo de Taylor de f en P (x0 , y0 ): f (x0 + h1 , y0 + h2 ) − f (x0 , y0 ) = Hf (x0 , y0 )(h) + R2 (h, (x0 , y0 )), lı́m h→0 ! ∂2f ∂2f h1 ∂ 2 x (x0 , y0 ) ∂y∂x (x0 , y0 ) Hf (x0 , y0 )(h) = 12 h1 h2 ∂2f ∂2f h2 ∂x∂y (x0 , y0 ) ∂ 2 y (x0 , y0 ) R2 (h, (x0 , y0 )) =0 khk2 Estudio del signo de Hf (x0 , y0 )(h). Completamos cuadrados en la forma cuadrática. λ1 0 La Matriz Hessiana en P (x0 , y0 ) es simétrica ⇒ diagonalizable. λ1 y λ2 sus valores propios, , det(H) = λ1 · λ2 0 λ2 det(H) < 0 PUNTO SILLA sign(λ1 ) 6= sign(λ2 ) det(H) = 0 Punto crı́tico degenerado λ1 y/ó λ2 = 0 Estudio local de la función En algunas direcciones es un máximo En algunas direcciones es un mı́nimo Estudio local de la función Estudio de derivadas sucesivas MÍNIMO LOCAL f (x0 + h1 , y0 + h2 ) > f (x0 , y0 ) det(H) > 0 Extremo local sign(λ1 ) = sign(λ2 ) ∂2f (x0 , y0 ) > 0 ∂2x ∂2f (x0 , y0 ) < 0 ∂2x MÁXIMO LOCAL f (x0 + h1 , y0 + h2 ) < f (x0 , y0 ) ∂2f (x0 , y0 ) = 0 ∂2x Este caso no posible 0 b det = −b2 < 0 b d











