Tema 4. Operación financiera

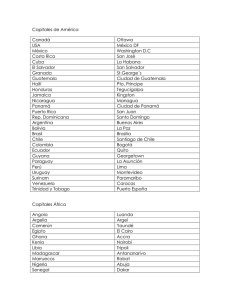
Tema 4. Operación financiera
1. Definición y clasificación
Se denomina operación financiera a todo intercambio no simultáneo de capitales
financieros pactado entre dos agentes, siempre que se verifique la equivalencia, en
base a una ley financiera, entre los capitales entregados por uno y otro.
Los elementos que intervienen en toda operación financiera son los siguientes:
a) Conjuntos de capitales que se intercambian. Se denominan, respectivamente,
prestación y contraprestación. La prestación está formada por todos los capitales que
entrega la parte que inicia la operación. La contraprestación está formada por todos
los capitales que entrega la parte contraria, esto es, la parte que recibe el primer
capital de la operación.
b) Agentes que intervienen en la operación: Se denominan prestamista y prestatario. El
prestamista es el que entrega la prestación y recibe la contraprestación. El
prestatario es el que recibe la prestación y entrega la contraprestación.
c) Duración de la operación: Es el tiempo que media entre el vencimiento del primer
capital (origen), entregado siempre por el prestamista y la entrega del último (final)
que, según la operación concreta, puede ser entregado por el prestamista o por el
prestatario.
d) Ley financiera de valoración: la operación financiera exige que los capitales
entregados por una y otra parte sean financieramente equivalentes según una ley
financiera explícita o implícita.
Las operaciones financieras pueden clasificarse según diferentes criterios, dando lugar a
múltiples modalidades no excluyentes entre sí:
a) Por la naturaleza de los capitales que intervienen en la operación:
Ciertas
‰ Aleatorias
b) Por su forma de definición
‰ Predeterminadas
‰ Posdeterminadas
c) Por su plazo
‰ A corto plazo
‰ A medio plazo
‰ A largo plazo
d) Por la distribución de los compromisos de las partes
‰ Simples
‰ Compuestas: Constitución, amortización, doblemente compuestas.
e) Por su sentido crediticio
‰ Crédito unilateral
‰ Crédito recíproco
f) Por la ley financiera utilizada
‰ De capitalización
‰ De descuento
g) Por el destino de los capitales entregados por las partes:
‰ Puras
‰ Con características comerciales
‰
1
2. Planteamiento general
Todas las operaciones pueden analizarse mediante un planteamiento común, basado en
la exigencia de que se verifique la equivalencia financiera entre los capitales entregados
por una y otra parte.
Así, dada una operación financiera cierta y doblemente compuesta, valorada con una ley
financiera de capitalización compuesta1 L( t; t n ) = (1 + i) t n − t y definida por:
Prestación: (C1 , t1 ), (C 2 , t 2 ), L , (C m , t m ) 


Contraprestación: (C1′ , t1′ ), (C′2 , t ′2 ), L , (C′n , t ′n ) 


Duración de la operación:  t1 ; t n  . Siendo t1 el origen de la operación y


t n = max  t m , t ′n  el final de la misma.


m
n
Debe verificarse que: (C h , t h )  ~ (C′k , t ′k )  en base a aquella ley.

 h =1 
 k =1
Si se elige un punto cualquiera τ, perteneciente al intervalo de duración de la operación,
τ ∈  t1 ; t ′n  , dicha equivalencia podrá expresarse mediante la exigencia de que las


sumas financieras de los capitales de la prestación y la contraprestación, obtenidas en
base a la ley financiera pactada (utilizando en este caso los factores), coincidan en dicho
punto. Esto es,
m
n
h =1
k =1
S = ∑ C h (1 + i)τ − t h = ∑ C ' k (1 + i)τ − t′k = S′
[1.]
Pτ = CPτ
donde:
S (Pτ): suma financiera en τ en base a ley L( t; t n ) = (1 + i) t n − t de todos los capitales
de la prestación.
S’ (CPτ): suma financiera en τ en base a ley L( t; t n ) = (1 + i) t n − t de todos los
capitales de la contraprestación.
(1 + i)τ − t h y (1 + i)τ − t′k : los correspondientes factores de capitalización y/o
contracapitalización.
La ecuación anterior, habitualmente denominada ecuación de equivalencia financiera,
exige que, en base a la ley pactada, la suma financiera del conjunto de capitales de
la prestación sea igual a la suma financiera del conjunto de capitales de la
contraprestación en cualquier momento τ.
Si se plantea dicha ecuación de equivalencia en el final de la operación, tn, y se pasan
todos los términos al primer miembro, se tendrá:
1
Este planteamiento es valido con cualquier tipo de ley financiera.
2
m
∑ C h (1 + i)
tn −th
h =1
n
− ∑ C 'k (1 + i) t n − t k = 0
k =1
[2.]
Esta ecuación permite realizar el análisis de cualquier operación financiera, sean cuales
fueren sus características, pudiendo obtener mediante su resolución tanto el parámetro i
de la ley financiera de capitalización compuesta que hace equivalentes prestación y
contraprestación, aunque la ley financiera en base a la que se acordó el intercambio no
se conociera, como la cuantía de algunos de los capitales que intervienen cuando el
parámetro i de la ley sea conocido.
Problema 1:
a) Determinación de la ley de la operación
El Sr. Pérez entrega 12.500€ al Sr. Martínez, el 20/06/2003 con el compromiso por
parte de éste de devolver tal cantidad en dos plazos de 6.438,12€, el 20/12/2003 y el
20/06/2004 ¿Cuál es la expresión de la ley de capitalización compuesta que sustenta
esta operación?
b) Determinación de algunos de los capitales de la operación
El Sr. Pérez entrega 18.000€ al Sr. Martínez el 15 de enero de 2003. ¿Cuál será la
cuantía que mensualmente deberá devolverle el Sr. Martínez en los próximos dos años,
si la operación se pacta en capitalización compuesta al 5,5% efectivo anual?
c) A la vista de la cuantía resultante el Sr. Martínez propone una operación alternativa
que consistiría en entregar 500€ mensualmente y una cuantía única a los dos años y
medio ¿Cuál sería el importe de esta cuantía si se mantuvieran las mismas condiciones
de valoración?
3. Reserva matemática. Concepto y métodos de cálculo.
3.1 Concepto y métodos de cálculo
La equivalencia financiera entre los capitales de la prestación y los de la
contraprestación sólo tiene que verificarse cuando se valoran todos los capitales que
constituyen la operación. Cuando lo que se valora es solo una parte de los mismos,
dicha equivalencia no tiene por qué verificarse y lo más frecuente es que no se
verifique.
Pues bien, el concepto de reserva matemática, o saldo financiero, se define como el
capital financiero que cuantifica la diferencia financiera existente entre los capitales
entregados por una y otra parte hasta un momento intermedio de la operación. Por tanto,
la reserva matemática también puede interpretarse como el capital que, entregado por la
parte que resulte deudora, restablece el equilibrio financiero de la operación en base a la
ley interna (o, en otras palabras, permitiría cancelar anticipadamente la operación).
A partir de esta definición la expresión que permitiría calcular la reserva matemática en
cualquier punto τ ∈  t1 , t n  será:


3
R τ = ∑ C h (1 + i)τ − t h − ∑ C′k (1 + i)τ − t′k = S1 − S'1
≤τ44244
≤τ44244
h1
3 k1
3
S1
( R τ = PPτ − CPPτ )
[3.]
S'1
Esta forma de calcular la reserva matemática recibe la denominación de método
retrospectivo, ya que valora la prestación y la contraprestación entregadas hasta el
momento de valoración τ.
Problema 2
Dada la operación financiera valorada en capitalización compuesta al 4% efectivo anual
y definida por los siguientes conjuntos de capitales
Prestación: (10.000,0), (5.000,3)(12.000,6) 


Contraprestación: (15.000,1), (11.565'12,5) 


Obténgase la reserva matemática en t = 4 por el método retrospectivo. Razónese el
resultado.
Sin embargo, como al final de la operación debe verificarse la igualdad de las sumas
financieras de todos los capitales de la operación, la reserva matemática puede
calcularse también por el denominado método prospectivo, que valora los capitales de
la prestación y la contraprestación que se entregarán desde τ hasta el final de la
operación.
R τ = ∑ C′k (1 + i) −( t′k −τ ) − ∑ C h (1 + i) −( t h −τ ) = S' 2 −S 2
k1
>τ44
>τ44
42444
3 h1
42444
3
S '2
( R τ = CPFτ − PFτ )
[4.]
S2
De forma que:
S1 – S’1 = S’2 – S2
S1 + S2 = S’1 + S’2
( PPτ − CPPτ = CPFτ − PFτ )
( PPτ + PFτ = CPPτ + CPFτ )
[5.]
[6.]
S = S’
que es la ecuación de equivalencia financiera que debe verificarse siempre que se
consideren todos los capitales de la operación.
Problema 3
Obténgase la reserva en t = 4 de la operación financiera del problema 2, utilizando el
método prospectivo.
La reserva obtenida de la forma descrita, en la que se valoran en el método retrospectivo
todos los capitales cuyo vencimiento es menor o igual que τ y en el prospectivo los
capitales con vencimiento mayor que τ, se denomina reserva por la derecha, R+, y es
la que se utiliza habitualmente. No obstante, en ocasiones puede resultar útil calcular lo
que se denomina reserva por la izquierda, R-, que consiste en valorar en el método
retrospectivo los capitales con vencimiento menores que τ y en el prospectivo los
capitales con vencimiento mayor o igual que τ. Así,
4
−
R τ = ∑ C h (1 + i)τ − t h − ∑ C 'k (1 + i)τ − t′k = ∑ C 'k (1 + i) −( t′k −τ ) − ∑ C h (1 + i) −( t h −τ )
h <τ
k <τ
k ≥τ
h ≥τ
[7.]
Naturalmente, si en τ no vence ningún capital la reserva por la derecha y por la
izquierda coincidirán. Si, por el contrario, en τ vence algún capital de la operación la
reserva por la derecha y por la izquierda serán distintas y se verificará:
R τ + = R τ − + Cτ − Cτ′
[8.]
Problema 4
Calcúlese la reserva en t =3, por la derecha y por la izquierda, de la operación financiera
del problema 2 utilizando el método prospectivo y el retrospectivo.
Cuando, conocida la reserva en un punto τ, se desea calcular la reserva en un momento
posterior τ ' , puede utilizarse el método recurrente, que no es más que el cálculo de la
reserva por el método retrospectivo, pero utilizando la valoración ya realizada al
calcular la reserva en el punto anterior τ. Así, si se calculara directamente la reserva en
τ ' por el método retrospectivo se tendría:
R τ ′ = ∑ C h (1 + i)τ ' − t h − ∑ C 'k (1 + i)τ ' − t′k =
h ≤τ ′
k ≤τ ′


= ∑ C h (1 + i)τ ' − t h + ∑ C h (1 + i)τ ' − t h −  ∑ C′k (1 + i)τ ' − t′k + ∑ C′k (1 + i)τ ' − t′k  =
h ≤τ
τ < h ≤τ ′
τ < k ≤τ ′
 k≤τ



= ∑ C h (1 + i)τ ' − t h − ∑ C k (1 + i)τ ' − t′k +  ∑ C h (1 + i)τ ' − t h − ∑ C′k (1 + i)τ ' − t′k  =
h ≤τ
k ≤τ
τ < k ≤τ ′
τ <h≤τ ′

= R τ+ (1 + i)τ ' −τ




τ '− th
τ '− tk 

+
− ∑ C′k (1 + i)
∑ C h (1 + i)
τ1
′ 2443 τ1
′ 2443 
< h4
≤ τ4
< k4
≤ τ4


S3
S '3


Es decir, la reserva en τ ' será igual a la reserva en τ valorada financieramente en τ '
más el saldo parcial de la operación en el intervalo ]tτ, τ ' ] valorado también en τ ' .
Problema 5: Calcúlese la reserva por la derecha en t =5 de la operación financiera del
problema 2 pero utilizando el método recurrente a partir de la reserva por la izquierda
en t =3.
5
3.2 Evolución de la reserva matemática
El examen de la evolución de la reserva constituye lo que se denomina el análisis
dinámico de la operación, lo que supone conocer en cada momento el sentido crediticio
de la misma a través de la valoración financiera de las posiciones de las partes.
Las funciones R τ + y R τ − varían al hacerlo τ dentro del intervalo  t1 , t n  según la


estructura concreta de la prestación y la contraprestación. Sin embargo, en toda
operación financiera la reserva tomará los siguientes valores extremos:
- En τ = t1 , origen de la operación:
R −t 1 = 0
R +t 1 = C1
-
En τ = t n , final de la operación:
R −t n
 '
'
C n si C n pertenece a la contraprestación
=
− C m si C m pertenece a la prestación
R +t n = 0
siendo C1 la primera de las cuantías de los capitales de la operación, que corresponde
por definición a la prestación, y C m o C 'n la última de las cuantías de los capitales de
la operación que puede corresponder, según el caso, a la prestación o a la
contraprestación.
La figura 1 representa la gráfica de la función reserva matemática de una hipotética
operación financiera de cinco periodos de duración en la que
(C , t ), (C , t ), (C , t )  representan los capitales de la prestación y
 1 1
2 2
5 5 


 '

'
(C 3 , t 3 ), (C 4 , t 4 )  los de la contraprestación.


C’3
C2
R1+ = C1
R2+
R3+
C’4
-
R 1=0
t1
t2
t3
t4
R4+
R5+= 0
t5
C5
R-5= -C5
6
4. Tanto efectivo de una operación financiera pura.
El interés por determinar el tanto efectivo de las operaciones financieras deriva de la
necesidad de obtener un parámetro indicativo de su coste o rendimiento que facilite la
comparación y la elección entre diversas alternativas que no estén definidas de forma
homogénea.
Se considera de forma generalizada que es el tanto efectivo de la ley de capitalización
compuesta la forma más adecuada de medirlo. Se entiende por tanto efectivo de una
operación financiera pura el tipo de interés efectivo anual de la ley de
capitalización compuesta que establece la equivalencia financiera entre la prestación y
la contraprestación de la operación, y se representa por ie.
Cuando la ley que define la operación es la capitalización compuesta con tipo de interés
constante, el propio parámetro de la misma informa del coste o rendimiento. Sin
embargo, en otros casos, el tanto efectivo no se conoce directamente y se hace necesario
proceder a su cálculo. Es decir, se deberá plantear nuevamente, en cualquier punto τ, la
ecuación de equivalencia entre prestación y contraprestación, pero considerando como
incógnita el tipo de interés anual de la ley de capitalización compuesta que hace que se
siga manteniendo dicha equivalencia. Veamos algunos casos:
a. La operación financiera se define con tipos de interés variables.
En una operación financiera de z períodos, en la que rigen respectivamente los tipos
de interés i1, i2, …, iz , se hace necesario calcular lo que se denomina tipo de interés
medio y que se define como el tipo de interés constante iM que aplicado en todos los
períodos de la operación en sustitución de i1, i2, …, iz, hace que se siga verificando la
equivalencia financiera de la operación. Es decir,
m
p
τ −th
∑ C h (1 + i M )
h =1
n
= ∑ C ck (1 + i M )τ − t k
k =1
[9.]
donde:
Chp y Ckc serán respectivamente los capitales de la prestación y de la
contraprestación calculados en base a los tipos de interés i1, i2, …, iz.
iM = ie el tanto efectivo de la operación pura.
Problema 6
El Sr. Martínez concierta una operación de préstamo el 10 de octubre de 2003 por
importe de 10.000€ comprometiéndose a devolver la cuantía prestada en tres plazos
anuales de igual cuantía. Si el tipo de interés de la ley de capitalización compuesta
pactada es del 4% anual el primer año, del 4,5% el segundo y del 5% el tercero,
obténgase:
a) Cuantía de los pagos anuales.
b) Tanto efectivo de la operación.
b. La operación está planteada en base a una ley que no es la capitalización
compuesta.
De forma similar al caso anterior, conocidos los capitales de la prestación y la
contraprestación obtenidos a partir de la ley pactada, se plantea nuevamente la
ecuación de equivalencia en capitalización compuesta y considerando como
7
incógnita el tipo de interés anual constante que permite que se siga verificando ésta.
Es decir,
n
p
τ −th
∑ C h (1 + i e )
h =1
m
= ∑ C ck (1 + i e )τ − t k
k =1
[10.]
donde:
Chp y Ckc serán respectivamente los capitales de la prestación y de la
contraprestación calculados en base a la ley pactada.
ie: el tanto efectivo de la operación pura.
Problema 7
Si el Sr. Martínez procede a descontar un capital de 5.000€ durante 90 días a un tipo
de descuento del 5% anual, obteniendo en el momento actual 4.938,36€. ¿Cuál sería
el tanto efectivo de la operación?
c. La ley interna de la operación es la capitalización compuesta, pero el tipo de
interés conocido no es el efectivo anual.
En este caso, bastará obtener el tipo de interés anual equivalente con las fórmulas
desarrolladas en el tema 2. Es decir:
m

j( m) 


i e = 1 + i ( m )  − 1 = 1 +
− 1 , dependiendo de cual sea el dato conocido,

m 




tipo de interés subperiodal o tipo de interés nominal.
m
Problema 8
Obténgase el tanto efectivo de una operación planteada en capitalización compuesta
al 10% nominal anual pagadero mensualmente.
5. Tanto efectivo de una operación con características comerciales.
5.1. Las características comerciales.
Cuando las operaciones financieras se contratan en los diversos mercados, de manera
adicional a los capitales que constituyen el intercambio financiero que define la
operación pura, suelen existir una serie de condiciones complementarias que modifican
la cuantía y/o el vencimiento de los capitales incluidos en la equivalencia inicial.
Estos elementos complementarios reciben la denominación de características
comerciales y se clasifican en dos grupos:
a) Características comerciales bilaterales. Son aquéllas que afectan a los dos
contratantes, modificando de igual forma, aunque naturalmente en distinto
sentido, sus compromisos.
Esto implica que, cuando en una operación sólo existen características
bilaterales, todas las cantidades entregadas por una parte son recibidas
íntegramente, y en el momento en que son abonadas, por la otra. Luego,
8

 

Pr estación real
Pr estación real

 

≅

 

(entregada por el prestamista )  ( recibida por el prestatario) 
y
 Contraprestación real   Contraprestación real


 


≅

(entregada por el prestatario)  ( recibida por el prestamista ) 
b) Características comerciales unilaterales: Aparecen cuando intervienen terceras
personas, que no son ni el prestamista ni el prestatario, que reciben o entregan
capitales a las partes de la operación. En este caso no se da la equivalencia
anterior y las cantidades entregadas por una parte no coinciden con las recibidas
por la contraria. Así,

 

Pr estación real
Pr estación real

 


≠

(entregada por el prestamista )  ( recibida por el prestatario) 
y/o
 Contraprestación real   Contraprestación real


 

≠

 

(entregada por el prestatario)  ( recibida por el prestamista ) 
La mayor parte de las características comerciales, bilaterales o unilaterales, suponen
modificaciones de las cuantías de los capitales intercambiados aunque también existen
características que modifican el vencimiento de los mismos.
Entre las que suponen modificación de las cuantías tienen especial importancia los
gastos, muy relevantes en algunas operaciones financieras, que, por lo general, corren a
cargo del prestatario y que pueden ser tanto bilaterales, es decir pagados a la parte
contraria (comisión de apertura, gastos de estudio, etc.), como unilaterales, si se pagan a
terceras personas (honorarios notariales, impuestos, etc.).
Menor importancia tienen las características que suponen entradas de capital.
Prácticamente se reducen a aspectos fiscales o subvenciones y sólo afectan a algunas
operaciones muy específicas.
5.2. Tantos efectivos de coste y rendimiento
La existencia de características comerciales obliga a distinguir entre la operación
financiera pura, que es aquélla en la que no existen o no se consideran las características
comerciales, y la operación financiera real.
Cuando existen características comerciales, el tanto efectivo de la operación pura deja
de ser representativo del coste o rendimiento de la operación al ser los capitales
intercambiados distintos a los que se consideran en el cálculo de éste. Por tanto, para
determinar el tanto efectivo real hay que definir nuevamente la prestación y la
contraprestación, esta vez en términos de los capitales realmente intercambiados y
9
referida además a cada uno de los contratantes, ya que, cuando existen características
unilaterales, son distintos para uno y otro.
Se denomina tanto efectivo real del prestamista, activo, o de rendimiento (ia), al tipo
de interés anual o tanto efectivo anual de la ley de capitalización compuesta que verifica
la equivalencia financiera entre la prestación real entregada por el prestamista y la
contraprestación real recibida por éste.
Prestación real
(entregada por prestamista)
~
ia
Contraprestación real
(recibida por prestamista)
Se denomina tanto efectivo real del prestatario, pasivo, o de coste, al tipo de interés
anual o tanto efectivo anual de la ley de capitalización compuesta que verifica la
equivalencia financiera entre la prestación real recibida por el prestatario y la
contraprestación real entregada por éste.
Prestación real
(recibida por prestatario)
~
ip
Contraprestación real
(entregada por prestatario)
En el supuesto de que las características comerciales fuesen todas ellas bilaterales, las
cantidades entregadas por cada parte coincidirían con las recibidas por la contraria y,
por consiguiente, los tantos efectivos del prestamista y del prestatario serían iguales y
existiría un único tanto efectivo de la operación.
ia = i p = ie
Prestación real
~
ie
Contraprestación real
6. Tantos efectivos utilizados en el mercado
En los distintos mercados en los que se contratan o negocian operaciones financieras es
frecuente que existan normas de funcionamiento que determinan la forma en que deben
calcularse los tantos efectivos de coste o rendimiento. Esto hace que los tantos efectivos
manejados en los mismos no siempre coincidan con las definiciones dadas
anteriormente. Las diferencias pueden derivar tanto de la ley utilizada para plantear la
equivalencia financiera, capitalización simple en vez de capitalización compuesta, como
de las características comerciales que se deben incluir en dicha equivalencia.
De entre las múltiples formulas utilizadas, destaca por su importancia y difusión el
denominado tanto anual equivalente (o tasa anual equivalente) TAE, aplicado para el
cálculo del coste o rendimiento de las operaciones bancarias. Para el cálculo del TAE se
utiliza la misma formulación financiera que en el caso del tanto efectivo, pero los
capitales incluidos en la equivalencia no siempre recogen todas las características
comerciales de la operación. De hecho, para cada operación concreta la norma indica
qué características deben incluirse o no incluirse. Es por ello que puede definirse el
TAE de una operación bancaria, como el tanto de coste de las operaciones activas y
el tanto de rendimiento de las pasivas, calculado según la normativa vigente.
En el momento actual, dicha normativa viene recogida en la Circular del Banco de
España 8/1990, de 7 de septiembre, sobre “Transparencia de las operaciones y
protección de la clientela”.
10
CUESTIONES TEÓRICAS.
1.- Razone si es verdadera o falsa la siguiente afirmación: “En toda operación
financiera la reserva por la derecha se diferencia de la reserva por la izquierda en
el importe del capital que vence en el momento del cálculo”.
2.- Razone si es verdadera o falsa la siguiente afirmación: “En una operación
financiera que sólo presenta características comerciales bilaterales, los tantos
efectivos de coste y rendimiento coinciden”.
3.- Razone si es verdadera o falsa la siguiente afirmación: “En toda operación
financiera la reserva por la derecha es siempre mayor que la reserva por la
izquierda, excepto en el final de la operación”.
4.- Razone si es verdadera o falsa la siguiente afirmación: “En una operación
financiera con características comerciales bilaterales y unilaterales, todas a cargo
del prestamista, el tanto efectivo de coste es distinto del tanto efectivo de
rendimiento, así como del tanto efectivo de la operación pura”.
5.- Razone si es verdadera o falsa la siguiente afirmación: “En las operaciones
financieras con más de un rédito de valoración, el tanto efectivo de la operación
pura se obtiene siempre calculando la media aritmética de los tipos de interés
aplicados”.
6.- Razone si es verdadera o falsa la siguiente afirmación: “En una operación
financiera doblemente compuesta, el prestatario siempre tendrá que abonar al
prestamista el saldo de dicha operación en el caso de cancelarse anticipadamente”.
7.- Razone si es verdadera o falsa la siguiente afirmación: “En una operación
financiera de amortización, la reserva por la izquierda en el origen de la operación
coincide con la cuantía del capital prestado”.
8.- Razone si es verdadera o falsa la siguiente afirmación: “Las operaciones de
amortización siempre son de crédito unilateral”.
9.- Denominando:
S1 = Cuantía de la suma financiera en τ de los capitales de la prestación con
vencimiento anterior o igual a τ.
S2 = Cuantía de la suma financiera en τ de los capitales de la prestación con
vencimiento posterior a τ.
S’1 = Cuantía de la suma financiera en τ de los capitales de la contraprestación con
vencimiento anterior o igual a τ.
S’2 = Cuantía de la suma financiera en τ de los capitales de la contraprestación con
vencimiento posterior a τ, obtenga:
a) La expresión del saldo financiero por la derecha ( Rτ+ ,τ) por el método
prospectivo en función de las variables anteriores.
b) Comentar el significado de la reserva cuando S2 > S’2.
11
10.- En una operación financiera con características comerciales bilaterales y
unilaterales a cargo del acreedor, razone si son verdaderas o falsas las siguientes
afirmaciones:
a) El tanto efectivo de rendimiento es distinto del tanto efectivo de coste.
b) El tanto efectivo de rendimiento es igual al tanto efectivo de coste.
c) El tanto efectivo de rendimiento es distinto del tanto efectivo de coste y ambos
distintos a su vez del tanto efectivo de la operación pura.
11.- En una operación financiera de amortización, razone si son verdaderas o
falsas las siguientes afirmaciones:
a) La reserva por la izquierda en el origen de la operación es cero.
b) La reserva por la izquierda al final de la operación es cero.
c) La reserva por la izquierda en el final de la operación coincide con la cuantía
del último capital de la contraprestación.
12.- Dada la siguiente operación financiera:
Prestación
C0
Contraprestación
CP1
CP2
CP3
CP4





t0
t1
t2
t3
t4
valorada en capitalización compuesta y siendo los réditos aplicables: i1 para los dos
primeros años; i2 para los dos últimos.
a) Establezca la ecuación de equivalencia que permitiría obtener la cuantía de la
prestación, conocidas las cuantías de la contraprestación.
b) Supuesta la existencia de un gasto inicial de naturaleza unilateral a cargo del
prestatario, Go, plantee la ecuación de equivalencia que permite calcular el
tanto efectivo pasivo de la operación.
13.- Dada la siguiente operación financiera:
Prestación
C3
C1
Contraprestación
CP2
CP4
CP5





t1
t2
t3
t4
t5
valorada en capitalización compuesta a un tipo constante i, señale si son
verdaderas o falsas las siguientes proposiciones y razónese la respuesta:
a) La reserva por la derecha en t2 por el método retrospectivo es (C1 - CP2)
b) La reserva por la izquierda en t3 es igual a la reserva por la derecha en t2
valorada en t3 menos la cuantía del capital de la prestación que vence en t3.
c) Está garantizado que la operación es de crédito bilateral.
12
14.- En una operación financiera de amortización cuyo esquema temporal es:
Prestación
C0
Contraprestación
a
a



t’0
t’1
t’2
.......
a
.......

......
t’S
a

......
t’n
valorada en capitalización compuesta a un tipo constante i, determine:
a) Saldo a entregar por el deudor en t’n-3 en el supuesto de cancelación anticipada
de la operación.
b) La reserva por la izquierda en t’s+1 a partir de la reserva por la derecha en t’s-1.
13