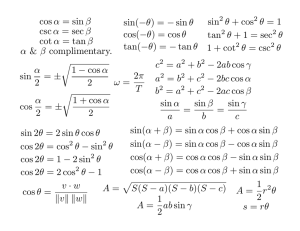Trigonometric Equivalences
Anuncio

Trigonometric Equivalences Common Values cos −θ Reciprocal Relationships = sec θ = cot θ = = sin(θ + π2 ) cos nπ = sin(nπ + π2 ) sin −θ = − sin θ csc θ cos cos θ = cos θ Quotient Relationships 1 sin θ 1 cos θ 1 tan θ √ π 6 π sin 6 π tan 6 Periods Angles vs. Signs tan θ = cot θ = sin θ cos θ cos θ sin θ = = = 3 2 1 2 √1 3 Pythagorean Relationships sin2 θ + cos2 θ = 1 1 + tan2 θ = sec2 θ 1 + cot2 θ = csc2 θ Subtraction Formulas Addition Formulas sin(α + β) = sin α cos β + cos α sin β sin(α − β) = sin α cos β − cos α sin β cos(α + β) = cos α cos β − sin α sin β cos(α − β) = cos α cos β + sin α sin β tan(α + β) = tan α+tan β 1−tan α tan β = tan α−tan β 1+tan α tan β Half-Angle Formulas Double-Angle Formulas sin 2α = 2 sin α cos α cos 2α = cos2 α − sin2 α = = 1 − 2 sin2 α = 2 cos2 α − 1 tan 2α tan(α − β) = 2 tan α 1−tan2 α Products of Sines and Cosines q 1 θ sin θ = ± 1−cos 2 2 q 1 θ cos θ = ± 1+cos 2 2 q 1 θ sin θ tan θ = ± 1−cos 1+cos θ = 1+cos θ = 2 1−cos θ sin θ Sum and Difference of Sines and Cosines sin α cos β = 12 [sin(α + β) + sin(α − β)] sin α + sin β = 2 sin 21 (α + β) cos 12 (α − β) cos α sin β = 21 [sin(α + β) − sin(α − β)] sin α − sin β = 2 cos 12 (α + β) sin 12 (α − β) cos α cos β = 12 [cos(α + β) + cos(α − β)] cos α + cos β = 2 cos 12 (α + β) cos 12 (α − β) sin α sin β = 12 [cos(α + β) − cos(α − β)] sin α + sin β Law of Sines = 2 sin 12 (α + β) sin 12 (α − β) Law of Cosines a b c = = sin A sin B sin C sin A sin B sin C = = a b c a2 = b2 + c2 − 2bc cos A b2 = a2 + c2 − 2ac cos B c2 = a2 + b2 − 2ab cos C Author: Martin Blais, 2009. This work is licensed under the Creative Commons “Attribution - Non-Commercial - Share-Alike” license.