potencia y sección áurea

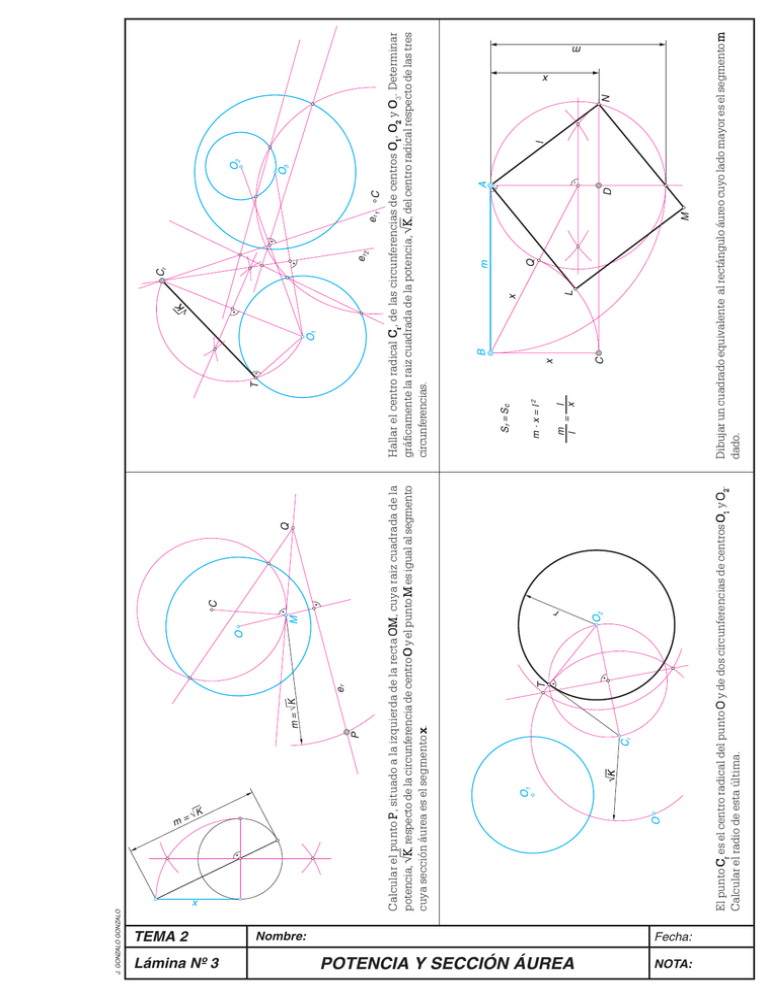
x
P
m = √K
er
O
M
C
Q
Nombre:
POTENCIA Y SECCIÓN ÁUREA
Fecha:
NOTA:
√K
Cr
T
O2
El punto Cr es el centro radical del punto O y de dos circunferencias de centros O1 y O2.
Calcular el radio de esta última.
O
O1
Calcular el punto P , situado a la izquierda de la recta OM
OM, cuya raiz cuadrada de la
K, respecto de la circunferencia de centro O y el punto M es igual al segmento
potencia, ÖK
cuya sección áurea es el segmento x.
J. GONZALO GONZALO
r
Lámina Nº 3
O1
er2
er1
C
O3
O2
C
x
L
x
Q
m
M
D
A
N
Dibujar un cuadrado equivalente al rectángulo áureo cuyo lado mayor es el segmento m
dado.
m
l
= x
l
m · x = l2
Sr = Sc
B
Hallar el centro radical Cr, de las circunferencias de centros O1, O2 y O3. Determinar
K, del centro radical respecto de las tres
gráficamente la raiz cuadrada de la potencia, ÖK
circunferencias.
T
√K
Cr
x
TEMA 2
m
√K
l
m=