Modelos Regionales de Interacción Espacial y Modelos

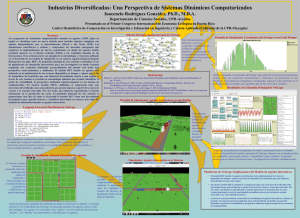
Modelos Regionales de Interacción Espacial y
Modelos Basados en Agentes: Una Aplicación
Computacional usando Sistemas de
Información Geográfica
Marcos Valdivia López1
Nelly Linares Sánchez2
José Antonio Huitrón Mendoza3
I.
INTRODUCCIÓN
Existe un número relativamente amplio de técnicas y métodos para analizar la
economía de una región. Desde la construcción de índices de localización y
concentración, hasta sofisticados modelos de econometría espacial. En este
capítulo discutimos una metodología denominada Modelos Basados en Agentes y
Simulación (MBAS), que ha tenido recientemente bastante aceptación en algunos
circuitos de la disciplina económica, dada su potencialidad para
modelar la
interacción entre agentes económicos heterogéneos, algo que por cierto ha sido
poco tratado en la disciplina dada su dificultad. De igual manera, en este capítulo
presentamos una aplicación de un modelo de interacción espacial de la zona
metropolitana de la Ciudad de México integrado a sistemas de información
geográfica, con el propósito de introducir al lector al terreno de la simulación
computacional en el área de la Economía Urbana y Regional.
El significado que tiene en la economía y en particular dentro de las
ciencias regionales el empleo de Modelos Basados en Agentes y Simulación
1
Investigador de tiempo completo adscrito al CRIM-UNAM y coordinador del proyecto “Un modelo
computacional de interacción espacial para explorar el crecimiento económico y las externalidades
tecnológicas e informativas de las zonas metropolitanas de la Región Centro” E-mail:
marcosv@correo.crim.unam.mx
2
Colaborador en el proyecto “Un modelo computacional de interacción espacial…”. E-.mail
neeslisa@yahoo.com.mx
3
Estudiante de la maestría en Economía en la FES-Acatlán y colaborador en el proyecto: “Un modelo
computacional de interacción espacial…”. E-.mail jose_eco71@yahoo.com.mx
1
(MBAS), es que nos permite estudiar, al momento de incorporar al espacio como
variable y dimensión en la actividad económica, fenómenos que tienden a ser
analíticamente intratables. Asimismo, los MBAS permiten al investigador tener
mayor flexibilidad en el planteamiento de los supuestos teóricos para modelar un
problema económico por que permite un mayor realismo a las premisas de las que
se parte para explicar un proceso, en contraste con los modelos abstractos (y
poco realistas) que son convencionalmente usados en el área de la economía
urbana y regional.
2
Antecedentes de los MBAS
Los MBAS4 han despertado interés en el campo de la economía porque permiten
modelar eficazmente la interacción entre individuos o agentes heterogéneos que
conforman un sistema económico. Aunque los MBAS no son una metodología que
surge de la disciplina económica, han sido incorporados en ésta porque han
mostrado gran utilidad tanto en los estudios de los mercados financieros, las
externalidades y específicamente en la interacción social de los agentes
económicos.
Si bien se pueden mencionar diversos estudios clásicos sobre el inicio de
los MBAS en las ciencias sociales (Axelrod 2007),5 quizás Epstein y Axtell (1996)
tengan el antecedente más importante del uso explícito de MBAS en la economía
al analizar la formación de precios, distribución del ingreso y segregación
residencial dentro de esta perspectiva.
La metodología de los MBAS sugiere una forma particular de estudiar la
economía, en comparación con el paradigma neoclásico que parte de una
estructura deductiva en la que se postula una serie de axiomas y supuestos para
modelar funcionalmente las relaciones entre variables que explican un proceso
económico, los MBAS en contraste privilegian un razonamiento inductivo al no
imponer una generalización (u homogeneidad) en las relaciones funcionales de las
variables y, con ello perseguir una mayor conexión con el comportamiento real de
los agentes económicos.6
En este sentido, la economía convencional [neoclásica] puede verse como
una teoría en donde los agentes toman decisiones –de cualquier índole–, para
maximizar beneficios individuales bajo condiciones de restricción o de recursos
escasos. Para garantizar que las decisiones de los agentes sean óptimas, la teoría
4
Los MBAS han sido utilizados para estudiar en particular complejidad; sin embargo, también
existen otros enfoques cercanos para analizar sistemas complejos en las ciencias sociales, por
ejemplo, modelos multi-agente, autómatas celulares, etc. Para ver una historia breve de este tipo
de modelos recomendamos ver el capítulo uno del libro de Nigel Gilbert y Klaus G. Troitzsch,
titulado: Simulación para las ciencias sociales.
5
Por ejemplo, el modelo de diseminación de la cultura propuesto por Axelrod (1997) –incluido en
Axelrod 2007–, es un clásico de cómo los MBAS pueden ser utilizados en el ámbito de la
antropología.
6
Algunos estudiosos consideran que los MBAS satisface varios de los principios de la postura
filosófica del “Realismo Científico” de Van Fraassen (Epstein, 1999)
3
económica
debe
asumir
ciertos
supuestos
sobre
el
comportamiento
y
características de dichos agentes. En particular, un supuesto importante en la
teoría es que los agentes sean homogéneos y que cada uno tome decisiones de
manera independiente, es decir, sin importar el comportamiento o decisiones de
los otros agentes. En este mundo ideal, las interacciones entre los agentes son
pasivamente mediadas a través de un sistema de precios y dividendos; es decir,
los consumidores y/o firmas son sólo tomadores de precios, que están dados, y
que por medio de un problema de decisión les permiten maximizar utilidad o
ganancia.
Así, los modelos económicos convencionales en general no admiten que
ocurran interacciones cara a cara y que exista interdependencia en las decisiones
de los agentes. Estas condiciones hacen pensar que las transacciones
económicas, las decisiones de los individuos, organizaciones, grupos o cualquier
tipo de expresión colectiva –todos estos pueden tener el carácter genérico de
agentes–, se llevan a cabo en un espacio explícito que influye sobre estos, y por
tanto de una mayor probabilidad de que exista heterogeneidad en el
comportamiento de dichos agentes.
A partir del producto de la interacción entre diversos agentes7 surgen los
resultados (agregados) que comúnmente estudiamos a partir técnicas como la
estadística o la econometría para el caso particular de los economistas. La
producción, la distribución y el consumo, en general, de la economía debe ser
entendida como una red extensa que se teje a partir de la interacción de una
cantidad
grande
de
agentes,
que
además
no
comparten
las
mismas
características.
Más adelante presentamos un ejercicio aplicado que aunque no puede
denominarse propiamente un MBAS, comparte muchos de los principios y
características de un MBAS que detallamos anteriormente. Al respecto, definamos
concretamente lo que es un modelo de esta naturaleza, siguiendo a Axelrod
7
Es preciso hacer énfasis que un agente en el contexto de esta metodología no se refiere al
individuo representativo del mundo neoclásico. Asimismo, en el contexto de la metodología de la
complejidad aplicada a las ciencias sociales y en particular en la economía un agente puede ser un
conjunto de empresas, una rama industrial, una organización, un sindicato, etcétera.
4
(2007: 93), “podemos decir que este tipo de simulación se caracteriza por la
existencia de muchos agentes los cuales interactúan con otros con una pequeña o
inexistente dirección central”, en un espacio explícito –pudiendo ser una
representación geográfica– y que siguen determinadas reglas de comportamiento
de acuerdo a sus cualidades y características particulares, tal interacción genera
resultados globales que dan cuenta de regularidades empíricas pudiendo éstas
estar consideradas dentro de alguna teoría existente –por lo general las reglas
parten de planteamientos teóricos previos–, o plantear nuevas rutas para
reflexionar sobre otras posibles explicaciones.
Es importante enfatizar en que la metodología de los MBAS contempla que los
sistemas sociales son de naturaleza descentralizada.8 Al decir que la economía no
tiene algún tipo de dirección podemos pensar en el ejemplo de la formación de
precios, la cual dista mucho de ser la historia walrasiana del subastador (véase
Tesfatsion (2005) y Albin y Foley (1998)) , por el contrario, procesos como la
formación de precios, los niveles de producción, las tasas de interés y todo aquello
que observamos de manera comúnmente agregada, son resultado de la forma en
que un número considerable de entidades económicas que, en lo particular
deciden, realizan transacciones y en general interactúan, para cumplir objetivos
particulares o colectivos.
II.
ELEMENTOS BÁSICOS DE UNA METODOLOGÍA DE INTERACCIÓN
DE AGENTES HETEROGÉNEOS
Este apartado consiste en presentar de manera sintética la metodología de los
MBAS. Partimos de la idea de que en economía –y en general en las ciencias
sociales– los fenómenos que se abordan son de naturaleza inestable, según
Gilbert y Troitzsch (2006: 15): “el objetivo [de estudio] es siempre una entidad
dinámica, que cambia a través del tiempo y reacciona a su entorno.”. En
cuestiones de Economía Regional, esto es aún más explícito dado que al tomar en
8
Aquí el planteamiento consiste en que al existir agentes heterogéneos, éstos asumen decisiones
y comportamientos que no dependen en lo absoluto de un ente que dirija o controle de manera
central la dirección de un sistema económico-social.
5
consideración sus componentes, se observa de manera más clara el carácter
dinámico que define los temas de estudios en esta área de investigación.9
El desarrollo de herramientas computacionales ha permitido que la
investigación en las ciencias sociales –y en particular en la economía regional–
tenga un campo más amplio de acción para generar mecanismos de validación de
teorías y de aplicación de modelos. No se concibe el uso de la metodología de los
MBAS sin el uso de las computadoras, la razón que explica esto la desarrollamos
a continuación.
En Gilbert y Troitzsch (2006), queda clara la diferencia entre los objetivos
de las técnicas de uso habitual y los MBAS cuando argumentan: “los modelos de
simulación se preocupan por procesos, mientras que los modelos estadísticos
típicamente tienen como meta explicar correlaciones entre variables medidas en
un punto singular en el tiempo” (ibídem. 18). Por ejemplo, cuando la estadística de
desempleo reporta una caída, ello nos lleva a pensar que en la economía existe
bajo dinamismo en determinados sectores como cierre de empresas, disminución
de la producción, caída de demanda externa o interna etc., que explican el
comportamiento agregado de esa variable. En los MBAS resulta posible modelar
este tipo de efectos que son vistos como procesos de interacción entre la
diversidad existente entre las empresas y trabajadores; por ejemplo, si un conjunto
de empresas importantes experimentan dificultades en un determinado ciclo ,
estos problemas pueden transmitirse a las empresas asociadas al sector,
pudiéndose contagiar –dadas las relaciones intersectoriales entre ellas– toda la
economía y esto generaría un impacto negativo en el nivel de empleo.
Al trabajar con modelos regionales podemos estudiar el comportamiento de
ciertas entidades y sus características económicas –municipios, empresas,
trabajadores, etc. – que coevolucionan en un marco de transformación dinámica
dentro del contexto donde se ubican. La distribución espacial de las entidades
modeladas está sujeta a las cualidades de la geografía; por ejemplo, los
asentamientos industriales se deben a razones como la proximidad entre las
9
Por ejemplo, el crecimiento urbano, la formación de nodos industriales, asentamientos
residenciales, dispersión en la producción de servicios, etc.
6
fuentes de insumos, los centros de comercialización o disposición de mano de
obra calificada, por lo que es imprescindible tener en consideración la estructura
geográfica de un lugar cuando se modelan las relaciones económicas y sociales
(Dibble, 2006); es decir, el espacio es también abordado como agente porque
imprime influencia sobre los resultados de un modelo dadas sus características
también heterogéneas, al contrario de los espacios isotrópicos que suponen los
modelos de Von Thünen y Alonso.
Los insumos básicos en la construcción de un MBAS son:
Agentes
Son entidades auto-contenidas10 que cuentan con características particulares
(personas, empresas, organizaciones políticas, municipios, países, etc.) y que a
partir de la interacción con otras pueden cambiar su estado en un sistema (por
ejemplo, una persona que está empleada pasa a desempleada o viceversa, o una
empresa en números rojos o negros, o países con déficit o superávit fiscal, etc.
Espacio (Ambiente)
Al hablar de procesos de interacción, los agentes se hallan situados en algún
punto del espacio, lo que les permite acceder a ciertos niveles de información,
tener un grado de “visión limitada del mundo” y establecer relaciones con
determinados actores cercanos o distantes de él11.
Reglas
En la construcción de un MBAS es importante asignar pautas de comportamiento
de los agentes analizados, de tal forma que permitan establecer de manera clara
cuáles son los patrones a seguir en sus decisiones individuales y en su
interacción. La construcción de reglas no es arbitraria ya que éstas en realidad
responden a normas asociadas a una visión teórica que permita involucrar
heterogeneidad entre estos agentes.
10
Castañeda (2010:6) define a un agente como una unidad auto-contenida porque: “presenta
reglas de comportamiento propias y autonomía de acción (auto-determinación y auto-activación), y
cuyo desempeño se manifiesta como producto de la interacción con otros agentes y con el entorno
en que se desenvuelve.”
11
Nigel Gilbert enfatiza: “Comúnmente, los ambientes representan espacios geográficos, por
ejemplo, en modelos sobre segregación residencial, donde el ambiente simula algunas
características físicas de la ciudad, y en modelos de relaciones internacionales donde el ambiente
son los mapas de Estados y naciones” (Cederman, 1997). [Así citado por Gilbert, 2008: 8]
7
Los tres componentes mencionados constituyen la estructura básica para la
construcción de MBAS. No está de más señalar que, factores como: el tema de
investigación, la teoría económica usada, y por supuesto, la habilidad y la
creatividad del investigador en manipular un software especializado en la
simulación del modelo, son condicionantes para alcanzar un MBAS confiable.
III.
ELEMENTOS PARA EL DISEÑO DE UN MODELO
Quizá la pregunta previa básica al incursionar en un MBAS dentro del análisis
económico gire en torno al nivel de simplificación que debe tener el modelo, dado
que la realidad socioeconómica es compleja y va más allá de un problema puro de
optimización individual, donde se asumen agentes relativamente homogéneos en
preferencias, tecnologías y hábitos. Además, se debe incorporar
la ubicación
geográfica de los agentes lo que influye en el intercambio de información, el nivel
de influencia de unos agentes sobre otros y en los resultados que se puedan
obtener en el agregado.
Los supuestos utilizados en la construcción de los MBAS, [es decir, la
reglas, el espacio y los agentes que uno impone en el modelo] deben, en primera
instancia buscar una conexión con la realidad investigada, pero también es
importante tener control de cómo (por qué) la construcción de un modelo de este
tipo puede eventualmente alterar o modificar las predicciones que comúnmente se
obtendrían bajo un esquema de modelación económica convencional. Por
ejemplo, el uso de los MBAS en la economía –aún bajo un esquema de agentes
optimizadores–, no tiende a producir un "equilibrio walrasiano" único, globalmente
estable y de rápida velocidad de convergencia (véase Tesfatsion, 2005).
A decir de Gilbert y Troitzsch (2006), el paso más complicado en la
construcción de un modelo de este tipo, es decidir que debe ser descartado e
incluido ; en este proceso de diseño, siempre debe tenerse presente el modelo
teórico en el cual nos estamos basando. Por ejemplo, ¿qué pasaría en una
discusión sobre la teoría del valor neoclásica si en un modelo walrasiano
convencional, 1) el subastador de precios (que permite conocer los precios de
equilibrio) es removido y, 2) si los precios y cantidades son ahora fijados por las
8
acciones de las propias firmas y consumidores? Como indica Tesfatsion (2006),
este pequeño cambio o perturbación conduce al modelo walrasiano a un terreno
de dificultades o incluso, de intratabilidad analítica. Este pequeño cambio en los
supuestos da origen a una serie de temas relevantes que, hoy en día se aceptan
en la ciencia económica como son la
información asimétrica, la interacción
estratégica, la formación de expectativas bajo condiciones de información limitada,
el aprendizaje mutuo, las normas sociales, los costos de transacción, las
externalidades, etc. (ibídem: 835).
En este mismo sentido Arthur (2008), considera que en la teoría general
del equilibrio neoclásico, lo que interesa es saber si los precios y cantidades de
bienes producidos o consumidos son consistentes con el patrón global de precios
y cantidades en los diversos mercados de la economía; de la misma forma, en el
enfoque de expectativas racionales, lo que interesa estudiar son los pronósticos o
expectativas consistentes con los resultados (económicos) que esos pronósticos o
expectativas generan. Dada la estructura analítica y los objetivos de la teoría
económica convencional, a partir de esta sólo es posible saber cómo son los
patrones globales de la economía, si estos estuvieran en equilibrio y de ese modo
suponer que son consistentes con el comportamiento individual de los agentes
(ibídem: 1554). Pero como bien señala Arthur, qué sucede si el comportamiento
de los agentes no es necesariamente consistente con el patrón global que el
primero genera; es decir, cómo se comportaría la economía si en realidad
estuviera siempre fuera de equilibrio (ibídem: 1154). Es en este punto donde un
enfoque computacional
o un modelo MBAS se vuelve metodológicamente
relevante, pues bajo esta perspectiva, lo que interesa
es modelar cómo las
acciones o estrategias (o expectativas) de los agentes diversos pueden
reaccionar, de manera endógena, a los patrones que ellos crean, y en donde, esas
reacciones son permanentes y pueden tener un carácter evolutivo.
En este sentido, un elemento importante es el proceso de adaptación que un
agente económico debe realizar como mecanismo para modificar sus estrategias o
acciones. En la literatura de los MBAS es común hallar la noción de un Sistema
9
Adaptable Complejo12 (CAS por sus siglas en inglés). De esta manera, sugerimos
que independientemente de la filiación teórica (y no sólo de aquellas de corte
neoclásico), los investigadores deberían analizar la economía como un CAS,
dadas las potencialidades de resolución de los problemas que ofrece esta
plataforma modelística y, en particular para los problemas tratados desde el
enfoque de la Economía Regional y Urbana.
IV.
APLICACIÓN DE UN MODELO REGIONAL DE INTERACCIÓN
ESPACIAL
En esta sección presentamos un ejemplo que simula con cartografía un modelo
sencillo para analizar el crecimiento económico regional como un proceso
territorial, espacial e interactivo. Se utilizan los principios básicos del Autómata
Celular (AC) para enfatizar el papel que juegan las relaciones espaciales13, las
cuales quedan definidas por la ubicación real relativa de cada unidad territorial que
conforma la región de estudio.
El ejemplo utilizado se refiere a la Zona Metropolitana del Valle de México
(ZMVM) definida por Conapo (2005) con 17 delegaciones del Distrito Federal, 1
municipio de Hidalgo y 58 municipios del estado de México. La regla de transición
aplicada es una versión continua del Voter Model desarrollada por Liggett (1985)
que modela efectos de contagio a partir de simples interacciones entre partículas o
unidades espaciales. En términos del ejemplo utilizado, lo anterior se traduce en
que la tasa de crecimiento local (
en el tiempo
de una unidad regional
(llámese municipio o delegación) está en función de la tasa de crecimiento
12
Podemos decir que un Sistema Adaptable Complejo no es una estructura que pueda ser
diseñada a priori, y que los resultados (o patrones) agregados que son observables son resultado
de una compleja red de interacciones que se da entre agentes heterogéneos que además se
retroalimentan positivamente al paso del tiempo, es decir, no hay manera de predecir con certeza
lo que ocurra en un tiempo determinado dada la naturaleza desequilibrante y diferenciada de sus
componentes.
13
La concepción de la localización como relaciones espaciales enfatiza que la distancia, el tipo de
vecindario, la configuración y/o propiedades del sistema en el cual se encuentren inmersos los
objetos de estudio son dependientes del tipo de interacción generada como consecuencia de la
distribución espacial y de los atributos de cada ubicación, lo cual permite explicar la variabilidad
entre diferentes unidades pertenecientes a un mismo sistema (Haining, 2003)
10
promedio de sus vecinos
en el tiempo t; tal como lo expresa la siguiente
ecuación:
A este modelo se le puede añadir un vector de parámetros (X) relacionados con
variables que teóricamente justifican su uso para analizar el crecimiento
económico regional (véase Capello, 2007), pero por cuestiones de simplificación
sólo analizaremos los resultados emergentes de un proceso interactivo en donde
la tasa de crecimiento inicial y la localización relativa, que define la cantidad y los
vecinos de cada unidad territorial, determinan el comportamiento de la tasa de
crecimiento del sistema metropolitano(
como:
Dada la naturaleza del ejemplo, el modelo se construyó en un programa
computacional, en este caso se utilizó la versión 4.1 de NetLogo, sin embargo en
la actualidad se pueden encontrar nuevas versiones como la 4.1.3 y la 5.0beta3.
Recomendamos bajar la versión 4.1.3 ya que la 5.0beta3 todavía se encuentra a
prueba. Este programa es un software libre de amplio uso para modelar las
interacciones entre agentes y, tiene la gran ventaja de que los agentes pueden ser
modelados con una localización o ubicación específica sobre un grid o cuadrícula.
Esto permite modelar, entre muchas cosas, autómatas celulares
14
con gran
sencillez. Asimismo, el programa permite integrar Sistemas de Información
Geográfica de tal forma que la cuadrícula o grid donde están ubicados los
agentes, pueda representar la "estructura geográfica real" de una ciudad o región
a través del uso de la cartografía. Netlogo es compatible con sistemas operativos
como Windows, Mac, OSX y Linux y se puede descargar de internet en la
siguiente página http://ccl.northwestern.edu/netlogo/g. A diferencia de otros
programas que permiten modelar interacción entre agentes (como Mathematica,
14
En su librería se pueden encontrar el modelo del Juego de la Vida y el de segregación de
Schelling
11
RePast, Phyton, etc.), Netlogo es muy sencillo y didáctico porque está hecho, de
tal forma que el usuario no necesita tener un conocimiento previo y sólido sobre
programación.
Para poder replicar el modelo, además de bajar e instalar el programa, se
necesita información vectorial de la ZMVM a nivel municipal en formato “shp”. La
forma de obtener dicha información es a través de la página de internet de INEGI
(www.inegi.gob.mx) en la sección de Marco Geoestadístico Nacional. Por este
medio se puede obtener información vectorial a nivel nacional expresada en
estados, municipios y localidades. Para obtener información referente a la ZMVM,
es necesario usar un paquete adicional como ArcView que permita “recortar” la
región de estudio y añadir la información relacionada con las tasas de crecimiento
económico de cada municipio y delegación. Todos los archivos que hagan
referencia a los datos vectoriales deberán colocarse en la misma carpeta en la
cual será guardado el archivo del programa que construiremos.
En la hoja principal, el usuario, al abrir Netlogo, encontrará tres pestañas:
interfaz, información y procedimientos (Interface, Information, Procedures). La
pestaña de información está diseñada para proveer de manera documental lo que
hace la simulación; la de procedimientos contiene el código del programa; y desde
la pestaña del interfaz podemos controlar y visualizar los procesos y resultados de
la simulación. El programa reconoce tres tipos de objetos (los cuales están
asociados a los agentes que deseamos modelar): turtles, patches, y links. Estos
tres objetos pueden contener información individual que caracteriza o describe a
los agentes. El ambiente espacial donde los agentes se desenvuelven es una
cuadricula (grid) bidimensional de color negro, donde cada celda representa un
patche; y, a diferencia de los patches, las tortugas (turtles) pueden moverse a
través de toda la cuadrícula.
El primer paso consiste en escribir las reglas que seguirán los agentes, para
ello hay que ubicarse en la pestaña de procedimientos, inmediatamente aparecerá
una hoja en blanco en la que es necesario escribir con la ayuda de primitivas de
NetLogo, las reglas de operación del programa de simulación propuesto. En
general, un procedimiento es una combinación de primitivas (estas son comandos
12
propios de NetLogo y, dentro de la programación se resaltan en color azul) que
sirven para estructurar un nuevo comando que permita la aplicación de ciertas
reglas de comportamiento que tendrán que aplicar los agentes modelados, y las
cuales deben estar constituidas al menos de tres partes:
1) Declaración de variables
2) Ajuste inicial
3) Actualización
En la primera parte hay que declarar si vamos a usar 1) alguna extensión (en
nuestro ejemplo utilizaremos las primitivas asociadas a GIS), 2) variables globales
y 3) como modelaremos diferentes clases de agentes es indispensable utilizar la
primitiva breed, con la intención de que cada clase tenga una serie de atributos
específicos. El código de esta primera parte para el ejemplo es el siguiente:
extensions [gis]
globals [municipios-dataset]
breed [municipios municipio]
munipios-own [cve_mpo nom_mun Gr #_vec, WGr]
La extensión GIS en Netlogo permite reconocer, dibujar y desplegar al mismo
tiempo sobre el grid del interfaz objetos vectoriales como puntos, líneas y
polígonos y datos tipo raster. Con esta extensión se pueden hacer desde
consultas hasta generar el centroide de un polígono. Una variable global es
aquella en la que un agente puede acceder en cualquier momento de la
programación. En este ejemplo necesitamos que los municipios o agentes
accedan a la información de la base de datos adjunta al archivo .shp que
denominaremos como [municipios-datset]. Cuando definimos alguna clase de
objeto es importante escribir el nombre del objeto en plural seguido de su singular.
Asimismo tenemos que definir los atributos de los agentes, y se puede utilizar
cualquier criterio desde palabras completas, claves, etc. En nuestro ejemplo,
utilizamos algunas abreviaciones; la clave (cve_mpo), nombre (nom_mun), tasa de
13
crecimiento del PIB (Gr), el número de vecinos de cada municipio (#_vec) y la tasa
de crecimiento promedio de sus vecinos (WGr).
La segunda y tercera parte se escriben en forma de comandos. Un
comando tiene que iniciar con la primitiva to seguido de un nombre para dicho
comando y terminar con la primitiva end. En el caso del ejercicio, el apartado de
ajuste inicial tiene la intención de declarar los comandos que nos permitan definir
las características del inicio de cada corrida, para ello construimos dos comandos:
setup y display-ZMVM. El procedimiento de la programación es el siguiente:
to setup
reset-ticks
ca
set municipios-dataset gis:load-dataset "zmcm_mgm09.shp"
display-ZMVM
end
La función de setup, en general, reinicia a cero el conteo de ticks; elimina
cualquier resultado de corridas previas sobre la cuadricula (ca); y define la variable
global [municipios-datset]. Esto se hace a través de una primitiva denominada
reporter, su función es calcular un resultado a partir de un insumo e informar de
ello. En términos más sencillos, lo que hace esta instrucción es renombrar la base
de datos adjunta al archivo “.shp” (“zmcm_mgm09.shp”) como [municipiosdataset]; y se crea un vínculo entre la base de datos y el lenguaje de NetLogo. La
penúltima línea es el segundo comando enumerado en el párrafo anterior, como
no existe una primitiva que nos permita desplegar la cartografía de la ZMVM
directamente se tiene que construir un comando adicional, el cual será invocado
en el momento en ejecutemos el comando setup.
El comando display-ZMVM, en términos de los procedimientos que
estamos modelando, es uno de los mas laboriosos pues incluyen una combinación
de primitivas de NetLogo y de la extensión GIS. El objetivo es hacer compatible la
información vectorial en el mundo de NetLogo. El camino es usar la primitiva
14
gis:draw que desplegará una representación cartográfica de la ZMVM: y la
primitiva gis:centroid-of, la cual genera un centro de gravedad o centroide por
cada polígono, los cuales, Netlogo reconocerá automáticamente como tortugas
con forma de circulo, de color verde y con un tamaño 1. En esta parte, además, se
definen las variables propias de cada municipio. El procedimiento es que cada
municipio retome la información de la base de datos de acuerdo a la variable y su
referencia geográfica, también podemos etiquetar a los “municipios” con alguno de
los atributos que hemos establecido en la programación como podría ser la clave
del municipio (set label cve_mpo).
La última etapa del código de display-ZMVM genera la información inicial
relacionada con la identificación del número de vecinos a partir de un radio de
distancia, el origen del radio se establece desde la posición de cada municipio;
una vez identificado el número de vecinos y sus vecinos se procede a calcular la
tasa de crecimiento promedio de estos que servirá como insumo en la simulación.
Es en esta etapa de la programación en la que se está implementando la ecuación
(2). El código es el siguiente:
to display-ZMVM
ask municipios [ die ]
gis:set-drawing-color white
gis:draw municipios-dataset 1
foreach gis:feature-list-of municipios-dataset
[let centroid gis:location-of gis:centroid-of ?
if not empty? centroid
[create-municipios 1
[ set xcor item 0 centroid
set ycor item 1 centroid
set shape "circle"
set size 1.5
set color green
15
set cve_mpo gis:property-value ? "CVE_MPO_"
set nom_mun gis:property-value ? "municipio"
set Gr gis:property-value ? "GAVGPIB"
set label cve_mpo ] ] ]
ask municipios [
set #_vec ((count municipios in-radius-nowrap distancia) - 1 )
set WGr (sum [Gr] of municipios in-radius-nowrap distancia - [Gr] of self) /
#_vec
]
End
Estos códigos nos permitirán visualizar la cartografía en la cuadricula una vez que
hayamos creado en la pestaña de interfaz unos botones que hagan referencia a la
variable global distancia. Esta variable no está definida dentro del procedimiento
pues queremos tener la libertad de utilizar diferentes parámetros. Para ello
ubicamos el icono con la palabra buttom lo oprimimos y seleccionamos la opción
slider, damos un click en el área en blanco donde se ubica el grid, aparece un
cuadro de dialogo y damos un nombre a la variable global (distancia), acotamos el
valor mínimo en 0 y el máximo en 20 y finalmente damos un click en ok. Para
crear un botón para el comando setup escogemos la opción buttom y escribimos
el nombre del comando, damos un click en ok.
Una vez que tenemos los dos botones, damos un click
en setup e
inmediatamente se desplegará una cartografía con centroides. Al dar un click
derecho sobre alguno de ellos inmediatamente se abrirá una ventana, si
seleccionamos la opción “inspect municipio” podremos verificar que la información
de la base de datos, la definición del número de vecinos a si como la tasa de
crecimiento promedio del PIB de los municipios vecinos de cada municipio se
habrá generado (véase figura 1).
Figura 1. Desplegando la información de cada municipio
16
Antes
de
proseguir
podemos
verificar
que
el
modelo
está
corriendo
adecuadamente con solo mover con el ratón la línea roja del slider y observar para
alguno de los municipios que el número de vecinos y la tasa de crecimiento de sus
vecinos va variando conforme van cambiando los valores de distancia. Para ello,
primero tenemos que escoger un valor, luego dar un click sobre setup y escoger
algún municipio y así sucesivamente.
La actualización, tercera y última parte del procedimiento consta de tres
comandos, y su objetivo principal es actualizar el estado de los municipios; esta es
la parte en donde la dinámica del modelo queda establecida. El primer comando
go a la vez incluye otros dos, actualización y do-plots, y comienza comprobando
si el proceso de interacción ha generado un efecto de contagio global, en el cual
todos los municipios tienen la misma tasa de crecimiento; si se cumple tal
condición el programa se detendrá automáticamente. La rapidez con la que
lleguen los municipios a esta condición de contagio global, dependerá en gran
medida de las interdependencias de interacción que queden establecidas a través
del umbral de distancia. Por ejemplo, si las vecindades están definidas por
umbrales pequeños en donde al menos un municipio quede aislado de los demás,
el efecto de contagio nunca se concretará; en contraste, si se definen vecindades
en las que se incluya a la mayoría de los municipios, el efecto de contagio se
generará en unos cuantos ticks o pasos de tiempo de la simulación. Una vez que
se ha verificado si se concretó el fenómeno de contagio generalizado, se pide al
17
programa que efectué los dos comandos restantes (i.e. actualizacion y do-plots), y
una vez que se ejecutan ambos, el sistema avanza un tick en el contador virtual
del tiempo de NetLogo.
to go
if ([WGr] of municipios = [Gr] of municipios) [stop]
ask municipios [actualizacion]
do-plots
tick
end
to actualizacion
set #_vec ((count municipios in-radius-nowrap distancia) - 1 )
set WGr (sum [Gr] of municipios in-radius-nowrap distancia - [Gr] of self) / #_vec
if breed = municipios [
set Gr ( WGr)
Ifelse Gr < mean [Gr] of municipios
[set color blue ]
[set color red]]
end
to do-plots
ask municipios [
set-current-plot "Gr"
plot mean [Gr] of municipios ]
end
El procedimiento actualización opera en tres fases: la primera define el vecindario
y la tasa de crecimiento promedio de sus vecinos, la segunda actualiza el valor de
la tasa de crecimiento de cada municipio en función de la tasa de crecimiento de
18
sus vecinos, y la tercera fase colorea a cada municipio de azul si queda por debajo
del promedio o rojo si está por encima del promedio. El número de vecinos queda
definido de acuerdo al umbral establecido dentro del interfaz denominado como
distancia. Respecto a la definición de las vecindades, es necesario tener algunos
elementos presentes. En un autómata celular clásico las vecindades son de primer
orden y están definidas de manera rectangular: Moore (8 vecinos) y Von Neuman
(4 vecinos). Los agentes que reconoce nuestro ejemplo son 76 puntos (que
corresponden al número de municipios y delegaciones que conforman a la ZMVM)
y que se ubicaran, de acuerdo a la información vectorial, en medio de una celda.
De esta forma las relaciones espaciales se establecerán a través de distancias.
Cada agente aplicará la distancia de manera multidireccional por lo que se formará
un área tipo circular, todos los puntos dentro de esta área serán los puntos con los
que cada agente conformará un vecindario y con los cuales interactuará. La
definición de la tasa de crecimiento de cada municipio en t+1 esta ponderada de
manera implícita y el valor del ponderador es uno. Pero al igual que la variable
global distancia podría generarse un slider para visualizar lo que sucedería cuando
el ponderador asume distintos valores. El ultimo comando do-plots define los
parámetros que tendrán que ser graficados, en este caso estamos interesados en
el comportamiento de la tasa de crecimiento de la ZMVM (ecuación 2), sin
embargo también podría graficarse la trayectoria de algún municipio en especifico.
Para finalizar, regresamos nuevamente al interfaz y creamos un botón
denominado go; en este caso activamos la casilla de forever; y una gráfica, en
donde el nombre de la grafica tiene que corresponder con el asignado en el
procedimiento, en este caso el nombre es “Gr”. Se tiene la opción de establecer
las etiquetas correspondientes al conjunto de las ordenadas al origen y las
abscisas, también se pueden establecer valores mínimos y máximos para estos,
etc. Una vez que hemos terminado de diseñar los nuevos objetos del interfaz
podemos realizar una corrida (ver figura 2), para ello damos un click en [setup] y
luego en [go]; el modelo parará automáticamente al momento en el que todos los
municipios hayan alcanzado el mismo valor en la tasa de crecimiento. Mientras
sucede esto se puede observar cómo van oscilando los valores de la tasa de
19
crecimiento de la ZMVM hasta llegar a un punto donde el modelo se estabiliza. Si
se corre la simulación varias veces obtendremos diferentes resultados, esto se
debe a que hay elementos que no se han controlado como la secuencia de
actualización. Aunque el modelo presentado es muy básico y general, permite
identificar algunas potencialidades que este tipo de modelos de interacción
espacial llevan implícitos para su desarrollo.
Figura 2. El modelo de tasa de crecimiento económico regional después de una
corrida
ACTIVIDADES
1. Genere un slider con el siguiente nombre pWGr, establezca como valor
mínimo “-1” y máximo “2”. Regrese a la tabla de procedimientos y en el
comando actualización sustituya la instrucción set Gr ( WGr) por set Gr
(pWGr * WGr) ¿Qué sucede con el modelo cuando le asignamos un valor
negativo? ¿Es estable? Pruebe con -1, 0, 0.5, 1 1.5
2. Una de las cualidades del modelo de simulación que construimos es que la
actualización se hace de manera secuencial, o sea que una vez que el
municipio A haya actualizado su valor, el resultado de B estará determinado
por
el
cambio
que
se
generó
en
A,
esta
forma
de
modelar
interdependencias es lo que genera los equilibrios múltiples. Sin embargo,
el modelo está muy acotado pues tras cada tick todos los municipios han
20
actualizado sin repetición ¿Qué pasaría si suponemos que tras cada tick
sólo un conjunto de municipios se actualiza? Para ello en la tabla de
procedimientos en el comando go sustituiremos ask por ask n-of 13. Varíe
el número hasta 76 ¿Qué sucede?
3. En NetLogo también podemos modelar fenómenos en los cuales no existe
una actualización continua, o sea que la información inicial sobre los
vecinos de cada municipio permanece invariable mientras se ejecuta todo el
procedimiento, para observar las diferencias genere un monitor en la
interface, y en la parte de reporter escriba lo siguiente: (mean [Gr] of
municpios) * 100. En la tabla de procedimientos sustituya ask n-of 13 por
ask-concurrent, Actualice la pantalla y corra varias veces el modelo con la
misma distancia ¿Qué sucede? Ahora establezca distancia en 31.
21
Base de datos
Municipio
PIB
Municipio
PIB
Venustiano Carranza
-5.39
Chicoloapan
13.82
Miguel Hidalgo
-0.17
Coyotepec
4.50
Cuauhtémoc
2.08
Chiautla
-1.24
Benito Juárez
-3.14
Cocotitlán
3.54
Xochimilco
-0.33
Melchor Ocampo
-2.71
Tlalpan
3.68
Nextlalpan
8.59
Tláhuac
1.71
Nopaltepec
9.32
Álvaro Obregón
7.29
Nicolás Romero
3.78
Milpa Alta
-7.90
Tepetlaoxtoc
-6.47
La Magdalena Contreras
9.53
Tepotzotlán
6.37
Iztapalapa
-3.84
Tepetlixpa
0.19
Iztacalco
-0.39
Tequixquiac
8.55
Gustavo A. Madero
-5.76
Texcoco
-0.97
Cuajimalpa de Morelos
7.34
Tezoyuca
12.11
Coyoacán
0.30
Villa del Carbón
8.24
Azcapotzalco
-7.63
Teotihuacán
9.07
Isidro Fabela
19.92
Teoloyucán
6.79
Huehuetoca
7.56
Tenango del Aire
-4.58
Hueypoxtla
13.39
Otumba
3.24
Ecatzingo
8.45
Tlalmanalco
1.07
Ixtapaluca
5.79
Temascalapa
5.32
San Martín de las Pirámides
4.46
Temamatla
-0.68
Tecámac
5.81
Tultitlán
0.93
Jilotzingo
15.40
Tultepec
-6.42
Jaltenco
16.13
Cuautitlán
-8.38
Ayapango
-3.11
Juchitepec
-2.59
Atlautla
20.18
Chalco
7.16
Coacalco de Berriozábal
8.55
Valle de Chalco Solidaridad
15.26
Axapusco
1.68
La Paz
3.29
Acolman
6.34
Nezahualcóyotl
-1.95
Papalotla
6.22
Ecatepec de Morelos
0.13
Ozumba
-0.60
Tlalnepantla de Baz
-2.71
Atizapán de Zaragoza
8.73
Naucalpan de Juárez
-0.78
Amecameca
-0.38
Huixquilucan
14.28
Atenco
9.24
Tonanitla
5.81
Apaxco
1.40
Zumpango
8.49
Chimalhuacán
7.26
Cuautitlán Izcalli
1.80
Chiconcuac
1.36
Tizayuca
5.06
22
REFERENCIAS
ALBIN, PETER Y FOLEY, DUNCAN (1998). Barriers and bounds to rationality:
essays on economic complexity and dynamics in interactive
systems. Princeton University Press, Estados Unidos.
ARTHUR, BRIAN (2008). “Out-of-equilibrium economics and agent-based
modeling” en Tesfatsion, Leigh y Judd Kennet (Eds.). Handbook
of computational economics, Volumen 2, Elsevier.
AXELROD, ROBET (2007). “Simulation in the social sciences”, en: Rennard, JeanPhilippe (Comp.) Handbook of Research on Nature-Inspired
Computing for Economics and Management, Volumen I, Idea
Group Reference, Estados Unidos.
CAPELLO, ROBERTA (2007). “A forecasting territorial model of regional growth:
the MASST model”, en The Annals of Regional Science, num.
41 (4), Berlin, pp. 753-787.
CASTAÑEDA, GONZÁLO (2010). Introducción a la sociomática. El estudio de los
sistemas adaptables complejos en el entorno socioeconómico.
El Colegio de México. Centro de Estudios Económicos. Mimeo.
DIBBLE, CATHERINE (2006). “Computational laboratories for spatial agent-based
models” en Tesfatsion, Leigh y Judd Kennet (Eds.). Handbook
of computational economics, Volumen 2, Elsevier.
EPSTEIN, JOSHUA (1999). “Agent-Based Computational Models and Generative
Social Science”. Complexity, Vol. 4, Num. 5, 41-60.
EPSTEIN, JOSHUA Y AXTELL, ROBERT (1996). “Growing Artificial Societies:
Social Science from the Bottom Up”, MIT Press, Estados
Unidos.
GILBERT, NIGEL Y TROITZSCH, KLAUS (2006). Simulación para las ciencias
sociales, Segunda Edición, McGraw Hill, Barcelona.
GILBERT, NIGEL (2008). Agent based models. SAGE Publications, Londres.
HAINING, ROBERT (2003). Spatial Data Analysis, Cambridge University Press,
Reino Unido.
TESFATSION, LEIGTH (2005). “Agent-based computational economics: a
constructive approach to economic theory”, Economics
Department, Iowa State University.
23