ACTIVIDAD 1 ... Suspensión de una rueda de ... remolque.
Anuncio

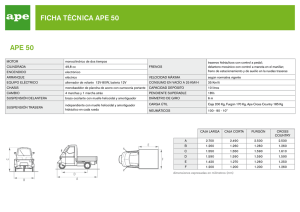
ACTIVIDAD 1 UNIDAD 10 Suspensión de una rueda de automóvil o de enganche de remolque. Esta actividad es un poco más larga y requiere una inmersión en matemáticas. No obstante, con un poco de esfuerzo y la ayuda de tu profesor puedes comprender la ventaja de reducir a analogías matemáticas los ejemplos físicos. La figura muestra un sistema consistente en un muelle y un amortiguador unidos a una masa sobre la que actúa una fuerza dependiente del tiempo. El objetivo es conseguir que el sistema sea "estable" para evitar oscilaciones que lo pongan fuera de control. x k.x m.a F(t) b.v m (b) Los datos del sistema muelle amortiguador son: k, constante elástica del muelle [N/m]. b, coeficiente de amortiguamiento viscoso [N.s/m]. (Puedes comparar esta expresión con la ley de Newton de la viscosidad vista en el capítulo anterior y observarás que son equivalentes). m, masa [kg]. f(t), fuerza dependiente del tiempo, que consideramos periódica de la forma f(t)=f0sen , donde f0, es la fuerza máxima [N]. 2 , pulsación [rad/s]. 2 . , con , periodo o tiempo en una oscilación [s]. , frecuencia o número de oscilaciones en la unidad de tiempo [s ó hertz]. La variable independiente es el tiempo, t [s], y la dependiente es el espacio, x [m], que es donde se desplaza la masa o sufre elongación; el resto de elementos son parámetros constantes del sistema; x es una función del tiempo x=x(t). Como variables derivadas tenemos la velocidad, v [m/s], que adquiere la masa, y la aceleración, a [m/s2]. v d x , que se lee: variación de la posición x con respecto al tiempo (derivada del espacio dt respecto al tiempo). a d d d d2 v x 2 x , que se lee: variación de la velocidad v con respecto al tiempo dt dt dt dt (derivada de la velocidad respecto al tiempo o derivada segunda del espacio respecto al tiempo). Las fuerzas que aparecen son: Fuerza recuperadora del muelle de módulo k.x (proporcional a la deformación). Fuerza de fricción viscosa (amortiguación, proporcional a la velocidad) de módulo b.v b. McGraw-Hill/Interamericana d x. dt Actividades Tecnología Industrial II. Bachillerato 1 de 3 Fuerza que da el producto m..a m d2 x (proporcional a la aceleración). dt 2 Fuerza excitadora f(t)=f0sen t Las condiciones iniciales del sistema son: Para t=0, x=0, f(t)=0, v=0, a=0. La aplicación de la ecuación de equilibrio de la mecánica f m.a , teniendo en cuenta el diagrama del sólido libre de la figura, es: f (t ) k.x b. d d2 x m. 2 x , dt dt que, para más comodidad, vamos a colocar así: m. d2 d x b. x k .x f (t ) 2 dt dt Es decir, en este sistema mecánico, la función de entrada es la fuerza f(t) que ejercen las irregularidades de la carretera y que provoca el desplazamiento o la fuerza del remolque sobre el coche tras un frenazo o acelerón, siendo la función de salida el desplazamiento x=x(t) que no conocemos. Un tipo de ecuación como que hemos obtenido se conoce como ecuación diferencial (conocemos la relación entre la variación de la variable dependiente respecto de la independiente y debemos calcular la función). Hay diversas teorías sobre la forma de resolverlo. Por ahora, solamente ten en cuenta que es preciso conocer las condiciones iniciales de t=0, aunque para nosotros en principio son siempre nulas. En el sistema de circuito RLC, la entrada es la tensión producida por un generador E(t), y la función que vamos a utilizar como salida es la carga almacenada en el circuito. Estos circuitos pueden entrar en resonancia tanto como en instalaciones industriales, en las que se trata de mejorar el factor de potencia con la colocación de condensadores. Se pueden producir sobreintensidades no deseadas ("inestabilidad"). L R C E(t) Los parámetros y datos del circuito son: R, resistencia en ohmios. La caída de tensión en la resistencia es VR=R.i L, coeficiente de autoinducción en henrys. La caída de tensión es VL C, capacidad en faradios. La caída de tensión es VC d i dt q 1 i.dt C C q, carga en culombios. McGraw-Hill/Interamericana Actividades Tecnología Industrial II. Bachillerato 2 de 3 i(t), intensidad en amperios. Debemos recordar que la intensidad es la variación de la carga con respecto al tiempo i d q o bien q i.dt . dt e(t), fuerza electromotriz en voltios. La ley de Kirchhof para las tensiones nos dice que la caída de tensión en los elementos del circuito es igual a la fuerza electromotriz. VL VR VC e(t ) L d2 d 1 q R i q e(t ) dt2 dt C Ahora observamos como esta ecuación es en todo semejante a la del sistema muelle amortiguador sin más que realizar las equivalencias: Sistema mecánico Sistema eléctrico m, masa L, autoinducción b, coeficiente R, resistencia amortiguación k, constante elástica del muelle 1 , inversa C de la capacidad x, desplazamiento q, carga v, velocidad i, intensidad F, fuerza aplicada E, fuerza electromotriz aplicada Tabla Analogías mecánicas y eléctricas. ¿Serías capaz de encontrar la función de transferencia de ambos sistemas utilizando la ecuaciones en forma de Laplace? McGraw-Hill/Interamericana Actividades Tecnología Industrial II. Bachillerato 3 de 3