A1 FAp 2014
Anuncio
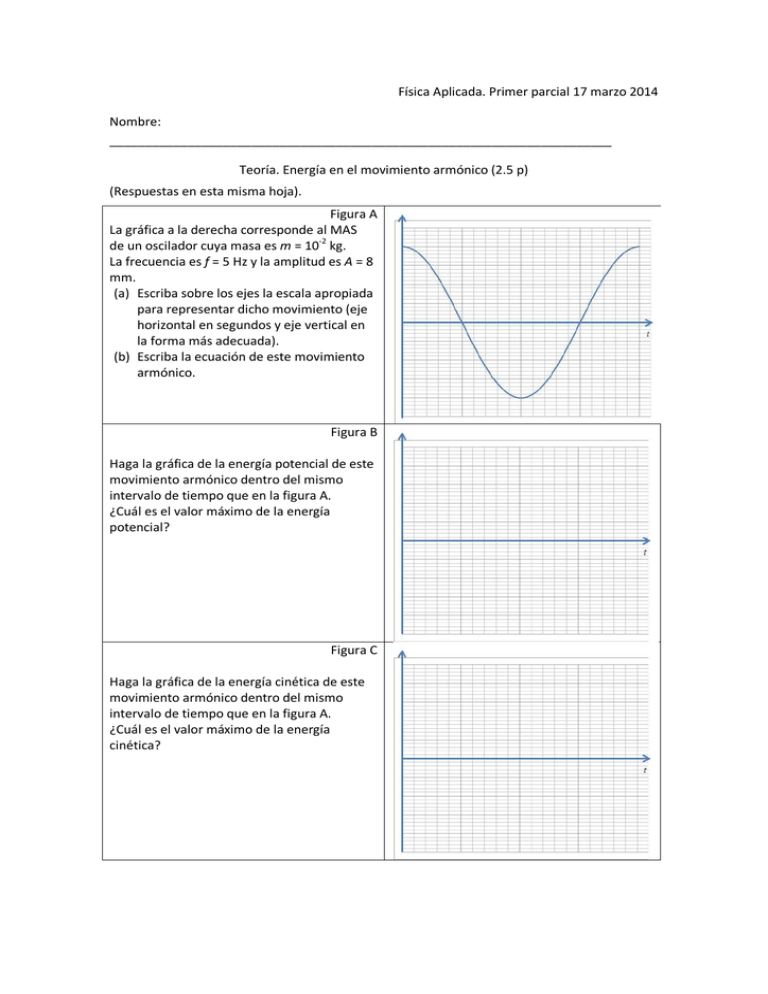
Física Aplicada. Primer parcial 17 marzo 2014 Nombre: _______________________________________________________________________ Teoría. Energía en el movimiento armónico (2.5 p) (Respuestas en esta misma hoja). Figura A La gráfica a la derecha corresponde al MAS de un oscilador cuya masa es m = 10-2 kg. La frecuencia es f = 5 Hz y la amplitud es A = 8 mm. (a) Escriba sobre los ejes la escala apropiada para representar dicho movimiento (eje horizontal en segundos y eje vertical en la forma más adecuada). (b) Escriba la ecuación de este movimiento armónico. Figura B Haga la gráfica de la energía potencial de este movimiento armónico dentro del mismo intervalo de tiempo que en la figura A. ¿Cuál es el valor máximo de la energía potencial? Figura C Haga la gráfica de la energía cinética de este movimiento armónico dentro del mismo intervalo de tiempo que en la figura A. ¿Cuál es el valor máximo de la energía cinética? Física Aplicada. Primer parcial 17 marzo 2014 PROBLEMAS (Pueden usarse libros y apuntes) PROBLEMA 1 (2 p) Un murciélago produce un ultrasonido de frecuencia 64000 Hz que es reflejado por objetos de tamaño semejante a su longitud de onda. Si la temperatura del aire donde se propagan las ondas es 10 ºC, (a) ¿cuál debe ser aproximadamente el tamaño de un insecto para que pueda ser detectado por el murciélago? (1 p) (b) Si la potencia emitida por el murciélago es 0.1 mW, determinar la intensidad a 10 m. (1 p) Datos del aire: = 1.40 = 8.314 J · mol K = 0.0289 kg · mol PROBLEMA 2 (2.5 p) (a) Calcular la amplitud de presión de una onda sonora de 500 Hz propagándose en helio si la amplitud de desplazamiento es 5·10-6 cm. (0.5 p) (b) Calcular el valor RMS de la presión, la intensidad y el nivel de intensidad de esta onda sonora. (1 p) (c) ¿Cuál es la máxima aceleración de una partícula en el medio donde se propaga esta onda sonora? (1 p) Datos del helio: velocidad del sonido = 972 m/s; densidad = 0.179 kg·m-3. Referencia nivel intensidad = 10-12 W·m-2. PROBLEMA 3 (3 p) Una cuerda flexible de 3 m de longitud, fija por sus dos extremos, está vibrando en el tercer armónico. El máximo desplazamiento de un punto de esta cuerda es 4 mm, y se sabe que la velocidad de propagación de las ondas transversales en ella es de 50 m/s. (a) Calcular la longitud y frecuencia de esta onda estacionaria. (1 p) (b) Escribir la ecuación de la onda estacionaria. (1 p) (c) Si la frecuencia de vibración se mantiene constante mientras se varía la tensión, ¿en cuánto debe cambiar la tensión para que aparezca el cuarto armónico? Expresar el resultado como porcentaje del valor de la tensión del tercer armónico. (Suponemos también que el hecho de cambiar la tensión no modifica la densidad lineal de masa). (1 p) THEORY SOLUTION. Graphics A The picture on the right shows the simple harmonic motion of an oscillator whose mass is m = 10-2 kg. Its frequency is f = 5 Hz and its amplitude is A = 8 mm. (a) Scale numerically the horizontal axis in seconds and the vertical axis in m in a suitable way. (b) Write the equation for this harmonic motion. Solution: f = 5 Hz T = 0.2 s = 10 rad/s = 8 · 10 cos(10 · ) (S. I. ) Graphics B Use the graphics paper on the right to plot the potential energy of this harmonic oscillator versus time within the same time range as in graphics A. What is the maximum value of potential energy? Solution: = Potential energy: = 1 2 =4 10 cos (10 ) Max. potential Energy: = 32 10 = = J = 3.16 · 10 J Graphics C Use the graphics paper on the right to plot the kinetic energy of this harmonic oscillator versus time within the same time range as in graphics A. What is the maximum value of kinetic energy? Solution: Total energy is constant and equal to Umax. = − 1 = − 4 10 cos (10 ) 2 The graph K vs t can be plotted without any calculation, note that U+K is always constant. PROBLEM 1 (2 p) A bat produces an ultrasonic echo (frequency 64000 Hz) which is reflected by objects whose size is similar to its wavelength. (a) If the temperature of the air where the waves propagate is 10 ºC, what is the approximate size of an insect so that it can be detected by the bat? (1 p) (b) If the power emitted by the bat is 0.1 mW, calculate the sound intensity at 10 m. (1 p) Air data: = 1.40 = 8.314 J · mol K = 0.0289 kg · mol SOLUTION (a) Speed of sound in air at 10 ºC → = The wavelength for sound of f = 64000 Hz is = . · . = = ·( . . ) = 337.6 m/s = 5.3 · 10 m We see that the size of insects the bat can detect by means this ultrasound is about 5 mm. (b) We assume that the emitted power spreads out over a spherical surface of radius r = 10 m. Then the sound intensity is 10 = = = 7.96 · 10 W · m 4 4 10 PROBLEM 2 (2.5 p) (a) Calculate the pressure amplitude of a 500 Hz sound wave in helium if the displacement amplitude is equal to 5·10-6 cm. (0.5 p) (b) What is the prms? Calculate the intensity and the intensity level of that wave. (1 p) (c) What is the maximum acceleration of a particle when this sound wave propagates? (1 p) Data of helium: speed of sound = 972 m/s; density = 0.179 kg·m-3. Reference intensity level = 10-12 W·m-2. SOLUTION (a) For f = 500 Hz Angular frequency =2 = 2 · 500 = 1000 rad/s Relationship amplitude pressure/displacement for sound waves = = 0.179 · 1000 · 972 · 5 · 10 = (b) Relationship pressure/intensity = . · √ Intensity level = 1.93 · 10 Pa = 10 · log The wave equation is ( , ) = = = = cos( . · · . √ = 2.15 · 10 · + ) − = ̈=− + ) cos( − This function reaches its maximum when cosine reaches its maximum: = ̈ = |− W·m = 3.23 rad/m − = . Pa = 63 dB · = ̇ = − (− ) sin( Second derivative yields acceleration = , where = = 10 · log (c) We calculate the wave number: Taking derivatives we get = = 2.73 · 10 | = 5 · 10 (1000 ) = 0.49 m · s + ) PROBLEM 3 (3 p) A string 3 m long and fixed at both ends is vibrating in its third harmonic. The maximum displacement of any point on the string is 4 mm. The speed of transverse waves in this string is 50 m/s. (a) What are the wavelength and frequency of this standing wave? (1 p) (b) Write the wave function of this standing wave. (1 p) (c) Assuming that the frequency of vibration is kept constant, how much should the tension in the string change to let the 4th harmonic to appear? Give the result as a percentage of the tension value for 3rd harmonic (assume that the mass per unit length remains constant as well). (1 p) SOLUTION (a) The 3rd harmonic in the string looks as shown in the figure: there appear three halfwavelengths in the string (both horizontal and vertical axis scaled in m). The standing wave condition to be satisfied is = Here n = 3 and the wavelength is 2 2·3 = = =2m 3 Wavenumber: 2 2 = = = m 2 Angular frequency: = · = 50 rad/s Frequency: = /2 = 25 Hz (b) The equation for the standing wave adopts the general form = sin for our 3rd harmonic we have = 0.004 sin sin 50 (S.I. units). sin . So (c) When the 4th harmonic appears we have four half-wavelengths in the string. The new wavelength is = = = = 1.5 m, therefore = = m . On the other hand, the angular frequency remains constant (4=3=50 rad/s) and what changes is the speed of waves. The relationship between the new tension T’ and the new speed v’ is = where is the mass per unit length, which remains constant. If we compare speeds and tensions in both cases, we obtain: For 3rd harmonic For 4th harmonic = = = = = We see that the tension must be reduced by 1 − / = = / = = , it is to say, 43.75%. =
