Capitulo 3a. Función Exponencial: Definiciones
Anuncio
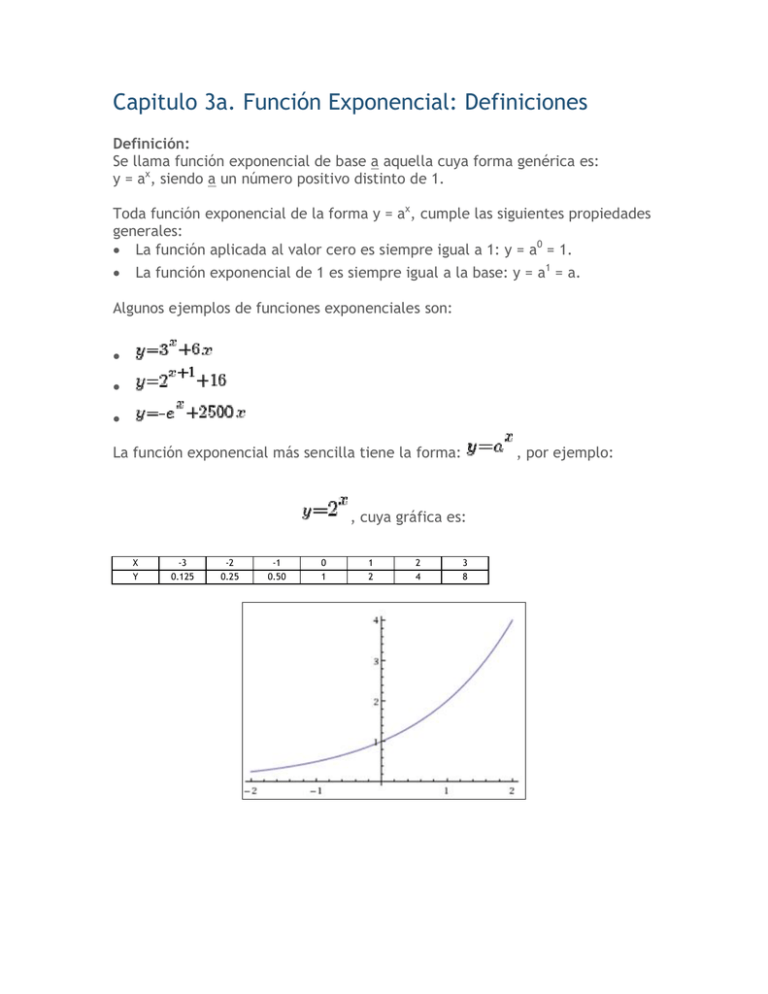
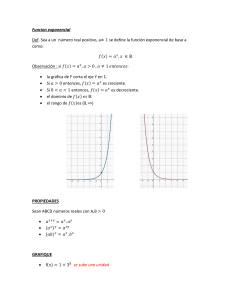
Capitulo 3a. Función Exponencial: Definiciones Definición: Se llama función exponencial de base a aquella cuya forma genérica es: y = ax, siendo a un número positivo distinto de 1. Toda función exponencial de la forma y = ax, cumple las siguientes propiedades generales: La función aplicada al valor cero es siempre igual a 1: y = a0 = 1. La función exponencial de 1 es siempre igual a la base: y = a1 = a. Algunos ejemplos de funciones exponenciales son: La función exponencial más sencilla tiene la forma: , por ejemplo: , cuya gráfica es: X Y -3 0.125 -2 0.25 -1 0.50 0 1 1 2 2 4 3 8 Algunas de las propiedades de y = ax son: Todas las gráficas intersecan en el punto (0,1) El eje x es la asíntota horizontal. Si a > 1, entonces y aumenta conforme aumenta x Si 0 < a < 1, entonces y disminuye conforme aumenta x La función exponencial de base e ( y = ex): Al igual que Π, e es un número irracional donde e = 2.71828… La notación e para este número fue dada por Leonhard Euler y esta constante es de importancia puesto que aparece en diferentes procesos administrativos como el interés compuesto. Algunas de las aplicaciones incluyen: El interés continuo. El capital obtenido de la inversión de un capital inicial a un interés compuesto sigue una ley exponencial Desintegración radiactiva. Las sustancias radiactivas se desintegran paulatinamente transformándose en otras clases de átomos y emitiendo energía y radiaciones ionizantes siguiendo una ley exponencial inversa. Crecimiento demográfico. Las curvas de crecimiento en una población sigue una ley exponencial