Solución semejanza
Anuncio

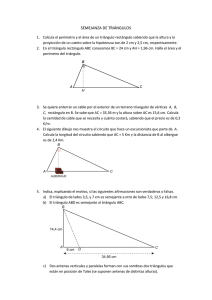
Matemáticas DEPARTAMENTO DE MATEMÁTICAS SEMEJANZA Nombre:……………………………………………………………………………… 1. Dos centímetros de un mapa equivalen a medio kilómetro sobre el terreno. (1 punto) a) ¿Cuál es la escala del mapa? ½ Km = 500 m = 50000 cm 2 cm ---------- -> 50000 cm 1 cm ---------- -> 25000 cm Escala 1:25000 b) Dos puntos del mapa distan en la realidad 35 Km. ¿Qué distancia los separará en el mapa? Distancia = ∙ 3500000 = = 140 cm 2. En un triángulo rectángulo las medidas de los lados son 3, 4 y 5 cm respectivamente. ¿Cuál debe ser el perímetro de un triángulo mayor semejante al anterior cuya razón de semejanza es 3? (1 punto) Si dos triángulos son semejantes, la razón de sus perímetros es igual a la razón de semejanza. ′ = 3 ⇒ = 3 Perímetro del triángulo original = 3 + 4 + 5 = 12 cm Perímetro del triángulo equivalente = 3 ∙ 12 = 36 cm 3. Los servicios de protección contra incendios de una comarca española emiten un informe sobre el número de hectáreas quemadas en el último incendio. En su mapa de escala 1:60000, la zona afectada tiene una superficie de 8 decímetros cuadrados. ¿Cuál es el resultado del informe? (Da el resultado en ) (1 punto) Razón de semejanza = Razón de semejanza entre las áreas = = ′ 1 = ⇒ = ∙ 60000 = 8 ! ∙ 60000 = 288 ∙ 10" ! 60000 = 288 #! 17 de febrero de 2010 Matemáticas DEPARTAMENTO DE MATEMÁTICAS 4. Se quiere enmarcar una fotografía de dimensiones 6 cm x 11 cm. Calcula las dimensiones del marco para que la razón entre el área del marco y el área de la fotografía sea 25/16. (1 punto) Razón de semejanza entre las áreas = Razón de semejanza entre las longitudes = Dimensiones del marco: 6 ∙ $ = 7,5 cm $ 11 ∙ $ = 13,75 cm 5. Se quiere construir un parterre con forma de triángulo rectángulo. Se sabe que la altura y la proyección de un lado sobre el lado mayor (hipotenusa) miden 15,3 m y 8,1 m, respectivamente. Calcula el perímetro y área del parterre. (1 punto) Parterre: Teorema de la altura: ℎ = ! ∙ ( ⇒ 15,3 = 8,1 ∙ ( ⇒ ( = , ", = 28,9 m Entonces la hipotenusa (x) medirá: 8,1 + 28,9 = 37 m Por el teorema de Pitágoras obtenemos los otros dos catetos: * = +15,3 + 8,1 = √299,7 = 17,31 m - = +15,3 + 28,9 = √1069,3 = 32,7 m Perímetro = 37 + 17,31 + 32,7 = 87,01 m Área = .∙, = 283,05 ! 6. Una piscina tiene 2,3 m de ancho; situándonos a 116 cm del borde, desde una altura de 1,74 m, observamos que la visual une el borde de la piscina con la línea del fondo. ¿Qué profundidad tiene la piscina? (1 punto) El siguiente dibujo representa la situación: 17 de febrero de 2010 Matemáticas DEPARTAMENTO DE MATEMÁTICAS Los triángulos ABC y CDE son semejantes, luego: , , = / ,.$ ⇒0 = ,.$∙, , = 3,45 m de profundidad 7. Un barco se halla entre dos muelles separados (en línea recta) 6,1 km. Entre ambos se encuentra una playa situada a 3,6 km de uno de los muelles. Calcula la distancia entre el barco y los muelles sabiendo que si el barco se dirigiera hacia la playa, lo haría perpendicularmente a ella. ¿Qué distancia hay entre el barco y la playa? (NOTA: El ángulo que forma el barco con los dos muelles es de 90º). (1 punto) Teorema de la altura: ℎ = ! ∙ ( ⇒ ℎ = 3,6 ∙ 6,1 − 3,6 = 3,6 ∙ 2,5 = 9 ⇒ ℎ = 3 Km es la distancia del barco a la playa Por el teorema de Pitágoras obtenemos las distancias del barco a los muelles: 0 = +2,5 + 3 = +15,25 = 3,91 Km al muelle 1 - = +3,6 + 3 = √21,96 = 4,69 Km al muelle 2 8. En un triángulo rectángulo se inscribe un rectángulo cuya base es dos veces su altura. Los catetos del triángulo miden 5 cm y 10 cm, respectivamente. Calcula las dimensiones del rectángulo. (1’5 puntos) 17 de febrero de 2010 Matemáticas 2 = . .32 DEPARTAMENTO DE MATEMÁTICAS ⇒ 35 − 104 = 74 ⇒ 35 = 174 ⇒ 4 = . = 2,06 cm Las dimensiones del rectángulo serán 2,06 cm de alto por 4,12 cm de largo. NOTA: Si los catetos se hubieran elegido de otra forma el problema se había exactamente igual y la solución sería un rectángulo de 1,84 cm de alto y 3,68 cm de largo. 9. Para medir la altura de una montaña, Pedro, de 182 cm de altura, se sitúa a 2,3 m de un árbol de 3,32 m situado entre él y la montaña de forma que su copa, la cima de dicha montaña y los ojos de Pedro se encuentran en línea. Sabiendo que Pedro se encuentra a 138 m del pie de la montaña, calcula la altura de la montaña. (1’5 puntos) / , = , ⇒ 0 = " "∙, , = 90 m Entonces la altura de la montaña será: 90 + 1,82 = 91,82 m 17 de febrero de 2010