ω π ω π ω π

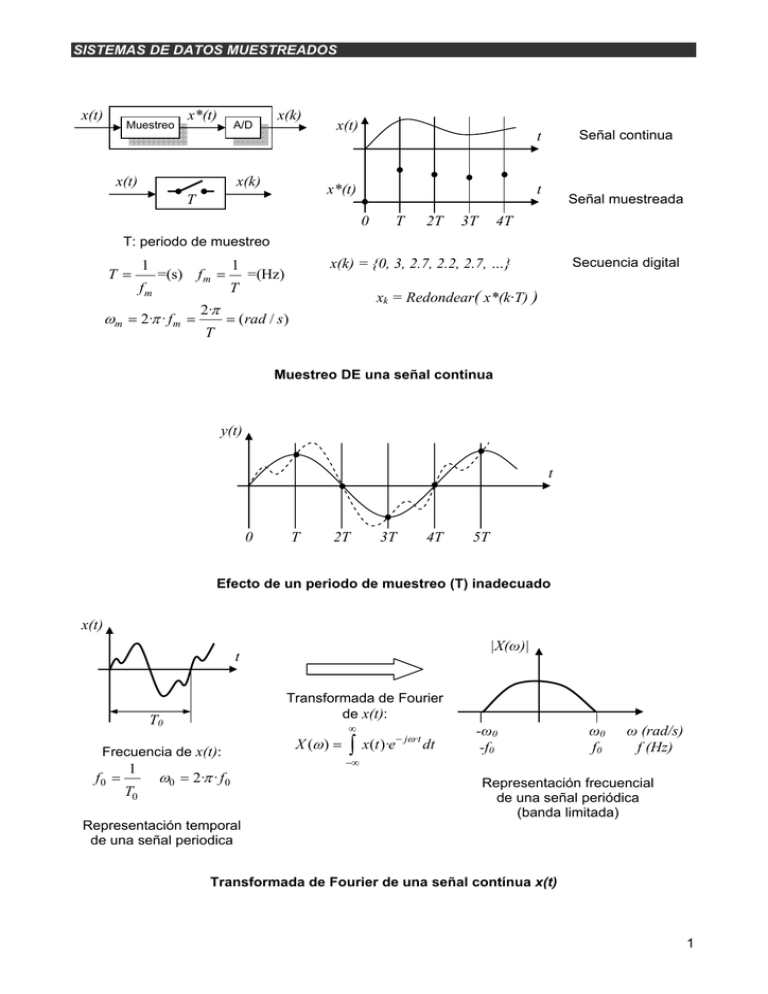
SISTEMAS DE DATOS MUESTREADOS
x(t)
Muestreo
x*(t)
A/D
x(t)
x(k)
x(k)
x(t)
t
x*(t)
T
Señal continua
t
0
T
2T
3T
Señal muestreada
4T
T: periodo de muestreo
T=
1
fm
=(s) f m =
ωm = 2·π · f m =
2·π
1
T
x(k) = {0, 3, 2.7, 2.2, 2.7, …}
=(Hz)
Secuencia digital
xk = Redondear( x*(k·T) )
= (rad / s )
T
Muestreo DE una señal continua
y(t)
t
0
T
2T
3T
4T
5T
Efecto de un periodo de muestreo (T) inadecuado
x(t)
|X(ω)|
t
Transformada de Fourier
de x(t):
T0
Frecuencia de x(t):
f0 =
1
T0
ω0 = 2·π · f 0
X (ω ) =
∞
∫
x(t )·e− jω ·t dt
-ω0
-f0
ω0
f0
ω (rad/s)
f (Hz)
−∞
Representación frecuencial
de una señal periódica
(banda limitada)
Representación temporal
de una señal periodica
Transformada de Fourier de una señal contínua x(t)
1
SISTEMAS DE DATOS MUESTREADOS
x*(t)
x(k) = {0, 1, -0.2, -1, …}
xk = x*(k·T)
t
Secuencia discreta
obtenida de x(t)
Transformada de Fourier de x(k)
0 T 2T 3T 4T
fm = 1/T
X k (ω ) =
|Xk(ω)|
k =∞
∑
k =−∞
xk ·e − jω ·k ·T
ω0
f0
- 3π /T
-3/(2T)
-fm·3/2
-2π /T
-1/T
-fm
-π /T
-1/(2T)
-fm /2
π /T
0
0
0
1/(2T)
fm /2
2π /T
1/T
fm
3π /T
3/(2T)
fm·3/2
ω (rad/s)
f (Hz)
f (Hz)
Transformada de Fourier de la secuencia discreta x(k)
π
T
Se pueden extraer |X(ω)| y x(t)
filtrando las componentes entre
-π /T y π /T
T suficientemente pequeño:
> ω0 →
1
T
> 2 f0 → fm > 2 f0
|Xk(ω)|
-π /T -ω0
-1/(2T) -f0
ω0 π /T
f0 1/(2T)
ω (rad/s)
f (Hz)
Transformada de Fourier de la secuencia discreta x(k) con T suficientemente pequeño
π
T
T demasiado grande:
< ω0 →
1
T
Se produce aliasing
No se pueden extraer |X(ω)| ni x(t)
< 2 f0 → f m < 2 f0
|Xk(ω)|
-ω0
-f0
-π /T π /T
-1/(2T) 1/(2T)
ω0
f0
ω (rad/s)
f (Hz)
Transformada de Fourier de la secuencia discreta x(k) con T demasiado grande
2
SISTEMAS DE DATOS MUESTREADOS
Para que el proceso de muestreo no suponga una perdida considerable de información, y
se pueda reconstruir la señal continua original a partir de la secuencia discreta de
muestras, es necesario que:
π
T
≥ ω0 o f m =
1
T
≥ 2 f0
Teorema del muestreo
|X(ω)|
ω (rad/s)
f (Hz)
|Xk(ω)|
-π /T
-1/(2T)
π /T
ω (rad/s)
f (Hz)
1/(2T)
Caso de una señal que no es de banda limitada
Interruptor
electrónico
x(t)
Convertidor
integrado
x*(t)
Vi
f0
Filtro paso-bajos para
evitar aliasing
T
C
A/D
Start
C retiene el último
valor capturado
mientras se
convierte
End
D0
·
·
·
D7
x(k)
Microcontrolador
Bus de
datos
μC
Señales de
control
Esquema de un circuito de muestreo y conversión A/D típico
3
SISTEMAS DE DATOS MUESTREADOS
x(k)
D/A
x*(t)
Bloqueador
x(t)
x(k) = {0, 1, 2, 1, 0, -1, -2, -1, 0…}
Secuencia digital
x*(k·T) = xk
x*(t)
x(k)
Bloq
t
Señal intermedia
x(t)
x(t)
T
t
Señal reconstruida
0 T 2T 3T 4T 5T 6T 7T
Reconstrucción de una señal a partir de una secuencia
x(t)
x(k)
T
Bloq
y(t)
T
y(t) será parecida a x(t) si se cumple el teorema de muestreo al
obtener x(k) y el bloqueador es el adecuado
Reconstrucción de una señal continua muestreada
4
SISTEMAS DE DATOS MUESTREADOS
x(k)
Sistema lineal
y(t)
Respuesta temporal a una secuencia impulso en la entrada:
y(t)=h(t)
x(k)=δ (k) = {1, 0, 0, 0, …}
La entrada se puede expresar como:
t
La salida se puede calcular como:
∞
∞
x(k ) = ∑ xn ·δ (k − n)
y (t ) = ∑ xn ·h(t − nT )
n=0
n =0
y(t)
x(k)={1, 2, 3}
t
T
2T
x0 · δ (k) = 1 · δ (k)
x1 · δ (k) = 2 · δ (k)
x2 · δ (k) = 3 · δ (k)
x0 · h (t)= 1 · h (t)
x1 · h (t) = 2 · h (t)
x2 · h (t) = 3 · h (t)
x(k)=1·δ (k)+2·δ (k-1)+3·δ (k-2)
y(t)= 1·h(t)+2·h(t-T)+3·h (t-T)
Modelado matemático de un sistema híbrido (I): respuesta a una secuencia impulso
Si se calculan las transformadas de
Fourier de las señales:
Y (ω ) = T.F. { y(t)} =
H (ω ) = T.F. {h(t)} =
∞
Y(ω) = H(ω) · Xk(ω)
y (t )·e − j ·ω ·t dt
∫
H(ω) es la función transferencia en
−∞
∞
∫ h(t )·e
− j ·ω ·t
dt
−∞
X k (ω ) = T.F. {x(k)} =
Entonces:
∞
∑
k = −∞
frecuencia, o respuesta en frecuencia
de un sistema
xk ·e − j ·ω ·k ·T
Demostración:
∞
∞ ⎛ ∞
∞
⎞
y (t ) = ∑ x n ·h(t − n·T ) → ∫ ( y (t ) )·e − j·ω ·t dt = ∫ ⎜⎜ ∑ x n ·h(t − n·T ) ⎟⎟·e − j·ω ·t dt →
n=0
⎠
−∞
−∞ ⎝ n =0
∞
∞ ⎛ ∞
⎞
→ ∫ ( y (t ) )·e − j·ω ·t dt = ∫ ⎜⎜ ∑ x n ·h(t − n·T ) ⎟⎟·e − j·ω ·(t − n·T ) ·e − j·ω ·n·T dt →
⎠
−∞
−∞ ⎝ n=0
∞
∞
∞
−∞
n=0
−∞
→ ∫ y (t )·e − j·ω ·t dt = ∑ x n ·e − j·ω ·n·T · ∫ h(t − n·T )·e − j·ω ·(t − n·T ) dt →
→ Y (ω ) = X k (ω )·H (ω )
Modelado matemático de un sistema híbrido (II): función transferencia en frecuencia
5
SISTEMAS DE DATOS MUESTREADOS
|X(ω)|
x(t)
t
Señal continua
original
-ω0
T0
Muestreo con periodo T
ω0
ω (rad/s)
|Xk(ω)|
Secuencia de
muestras
x(k) = {0, 1, -0.2, -1, …}
xk = x*(k·T)
-2π/T -π/T -ω0
Reconstrucción con
H(ω)
ω0 π/T 2π/T
ω (rad/s)
|H(ω)|
ω (rad/s)
Y(ω) = H(ω) · Xk(ω)
-π/T
π/T
|Y(ω)|
y(t)
Señal
reconstruida
-π/T -ω0
ω0 π/T
ω (rad/s)
Proceso de reconstrucción con un bloqueador ideal
h(t ) = T .F .−1{H (ω )} =
senω 0 ·t
ω 0 ·t
∞
∞
senω 0 ·(t − n·T )
n=0
n=0
ω 0 ·(t − n·T )
y (t ) = ∑ x n ·h(t − n·T ) = ∑ x n ·
Para calcular un valor de y(t) en cualquier instante t, hacen falta todos
los valores de x(k): {x0, x1, x2, ...} → No es causal
El bloqueador ideal no se puede llevar a la práctica
Función transferencia del un bloqueador ideal
6
SISTEMAS DE DATOS MUESTREADOS
x(k)
x(k) = {0, 2, 1, -1, ...}
y(t)
BOC
x*(t)
T
x(k)
t
xk
y(t)
ZOH
Secuencia digital
xk+1
T
x(t)
y(t) = x*(k·T) = xk
para k·T ≤ t < (k+1)·T
t
0
T
2T
3T
kT
(k+1)T
Señal intermedia
generado con los
valores de una
secuencia
Señal reconstruida
Funcionamiento del bloqueador de orden cero
δ (k)
SI x(k) = δ(k) = {1, 0, 0, 0, ...} → y(t) = h(t)
∞
1 − e − j·ω ·t
H (ω ) = T.F.{h(t )} = h(t )·e − j·ω ·t dt =
h(t)
BOC
∫
T
j·ω
−∞
|H(ω)|
Bloqueador ideal
h(t)
No permite reconstruir una
señal de forma perfecta
1
t
T
-6π/T -4π/T -2π/T -π/T π/T 2π/T 4π/T
6π/T ω (rad/s)
Función transferencia en frecuencia del bloqueador de orden cero
Microcontrolador
Convertidor
integrado
x(k)
μC
Bus de
datos
D0
·
·
·
D7
i(t)
D/A
Activar valor
Io
Convertidor
corriente a
tensión
Interruptor
electrónico
Amplificador
x*(t)
x(t)
T
C
C retiene el último
valor generado
Esquema de un circuito de conversión D/A típico con bloqueador de orden cero
7
SISTEMAS DE DATOS MUESTREADOS
u*(kT)
y(t)
u(t)
Computador
t
t
u(k)={1,1,2,3,1,2…}
t
Sistema
continuo
BOC
Referencia
r(k)={2,2,2,… }
Control
Salida
T
y(k)={1,2,3,2,2… }
T
y*(kT)
t
Sistema simple de control digital
Sistema discreto
equivalente
Computador
u(k)
u(k)
Referencia
r(k)
Ge(z)
y(k)
y(k)
Modelo matemático del sistema de control digital
u(k)
Sistema
discreto lineal
y(k)
Definición: Si u(k)= δ (k) entonces y(t)=g(k)
Utilidad: y (k ) =
∞
∑ un · g ( k − n ) ( g ( k − n ) = 0
n > k)
n =0
Definición: Si u*(kT)= δ (t) entonces y*(kT)=g(kT)
u*(kT)
Sistema
discreto lineal
y*(kT)
Utilidad:
∞
y (kT ) = ∑ u (nT )·g (k ·T − n·T )
( g ((k − n)·T ) = 0
n > k)
n=0
Concepto de la secuencia ponderación extendido a secuencias de muestras
8
SISTEMAS DE DATOS MUESTREADOS
u(k)
y(k)
Sistema
discreto lineal
U(z)
U(z) = Z{u(k)}
Y(z) = Z{y(k)}
Sistema
discreto lineal
Y(z)
Y(z){1 + a1·z-1 + ··· + an·z-n} =
= U(z){b0 + b1·z-1 + ··· + bm·z-m}
Ecuación en diferencias:
y(k) + a1·y(k-1) + ··· + an·y(k-n) =
= b0·u(k) + ··· + bm·u(k-m)
Y ( z) =
b0 + L + bm z − m
1 + aa z −1 + L + an z − n
·U ( z ) = G ( z )·U ( z )
Obtención de una función transferencia G(z)
δ (k)
δ*(kT)
Sistema discreto
lineal (Ec. Dif.)
g(k)
1
Z{δ (k)}=1
g*(kT)
Sistema discreto
lineal (G(z))
G(z)
G(z) = Z{g(k)} = Z{g*(kT)}
Otra forma de definir la función transferencia G(z)
x(t) ⇔ x(k)
Muestreo cada T segundos
xk = x(k·T)
Transformada de Laplace
Transformada de Fourier
∞
X (ω ) = F {x(t )} = ∫ x(t )·e − j·ω ·t dt
s=j·ω
∞
X ( s ) = L{x(t )} = ∫ x(t )·e − s·t dt
−∞
0
ω = 2·π · f (rad/s)
s = a + bj ∈ C
Transformada discreta de Fourier
Transformada discreta de Laplace
∞
∞
X k (ω ) = F {x(k )} = ∑ x k ·e − j·ω ·k ·T
X k ( s ) = L{x(k )} = ∑ x k ·e − s·k ·T
k = −∞
z = e j·ω·T
k =0
Transformada Z
z = e s·T
∞
X ( z ) = Z {x(k )} = ∑ x k · z − k
k =0
z = a + bj ∈ C
Relaciones entre las distintas transformadas
9
SISTEMAS DE DATOS MUESTREADOS
x(k)
δ(k)
Xk(s) = L{x(k)}
Y(s) = L{y(t)}
H(s) = L{h(t)}
y(t)
Sistema híbrido
lineal
h(t)
X(s)
Y(s)
H(s)
Y(s) = H(s)·Xk(s)
x(t)
δ(t)
X(s) = L{x(t)}
Y(s) = L{y(t)}
G(s) = L{h(t)}
y(t)
Sistema híbrido
lineal
g(t)
X(s)
Y(s)
G(s)
Y(s) = G(s)·X(s)
Modelo matemático de un sistema híbrido o continuo con la transformada de Laplace
H(ω) H(s)
u(k)
BOC
Del
computador
T
G(s)
u(t)
y(t)
Sistema
continuo
Salida
y(k)
Ge(s) = H(s)·G(s)
H (ω ) =
1− e
− j ·ω ·T
j·ω
→ H ( s) =
1− e
− s ·T
s
T
Al
computador
( s = j·ω )
De la relación entre la respuesta a un impulso de un sistema híbrido y su función transferencia:
u(k) = δ(k)
Ge(s)
y(t) = h(t)
Respuesta a
un impulso
Ge(ω) = F{h(t)}
h(t) = F-1{Ge(ω)}
Ge(s) = L{h(t)}
h(t) = L-1{Ge(s)}
De la relación entre secuencia ponderación y función transferencia en z:
Secuencia ponderación
u(k) = δ(k)
Ge(s)
y(t) = h(t)
y(k)=h(k)
T
Ge(z)
h(k): hk = h*(kT)
hk = h*(kT) = h(kT)
Ge(z) = Z{h(k)} = Z{h*(kT)} = Z{h(kT)} = Z{ L-1{Ge(s)} } = Z{ L-1{H(s)·G(s)} }
⎧⎪ −1 ⎧⎪1 − e − s·T
⎫⎫
⎪⎪
Ge( z ) = Z ⎨ L ⎨
G ( s ) ⎬⎬
s
⎪⎩ ⎪⎩
⎭⎪⎭⎪
Proceso para el modelado matemático del sistema de control digital
10
SISTEMAS DE DATOS MUESTREADOS
Sistema discreto
equivalente
Computador
Referencia
r(k)
e(k)
+
u(k)
Gc(z)
y(t)
Ge(z)
y(k)
R(z)=Z{r(k)} E(z)=Z{e(k)} Y(z)=Z{y(k)}
E ( z ) = R( z ) − Y ( z )
⎫
R( z )
⎬ → E ( z ) = R ( z ) − E ( z )·Gc ( z )·Ge( z ) → E ( z ) =
Y ( z ) = E ( z )·Gc( z )·Ge( z ) ⎭
1 + Gc( z )Ge( z )
R( z )
Gc( z )Ge( z )
Y ( z) =
Gc( z )Ge( z ) =
R( z )
1 + Gc( z )Ge( z )
1 + Gc( z )Ge( z )
Y ( z)
Gc( z )Ge( z )
=
Gbc ( z ) =
R( z ) 1 + Gc( z )Ge( z )
Modelo matemático discreto del sistema de control digital al completo
r(k)
y(t)
+
Gc(z)
H(s)
-
G(s)
BOC
y(k)
M(z)
T
Gbc ( z ) =
Y ( z)
R( z )
=
Ge(z)
Gc( z )Ge( z )
1 + Gc( z )Ge( z ) M ( z )
r(k)
y(t)
+
Gc(z)
H(s)
-
G(s)
BOC
y(k)
M(z)
N(s)
T
Ge(z)
{
}
Gee( z ) = Z L−1 { H ( s )G ( s ) N ( s )} → Gbc ( z ) =
Y ( z)
R( z )
=
Gc( z )Gee( z )
1 + Gc( z )Ge( z ) M ( z )
Otros casos que consideran la función transferencia del sensor (M(z) y N(s))
11