E07. Circuitos de corriente continua

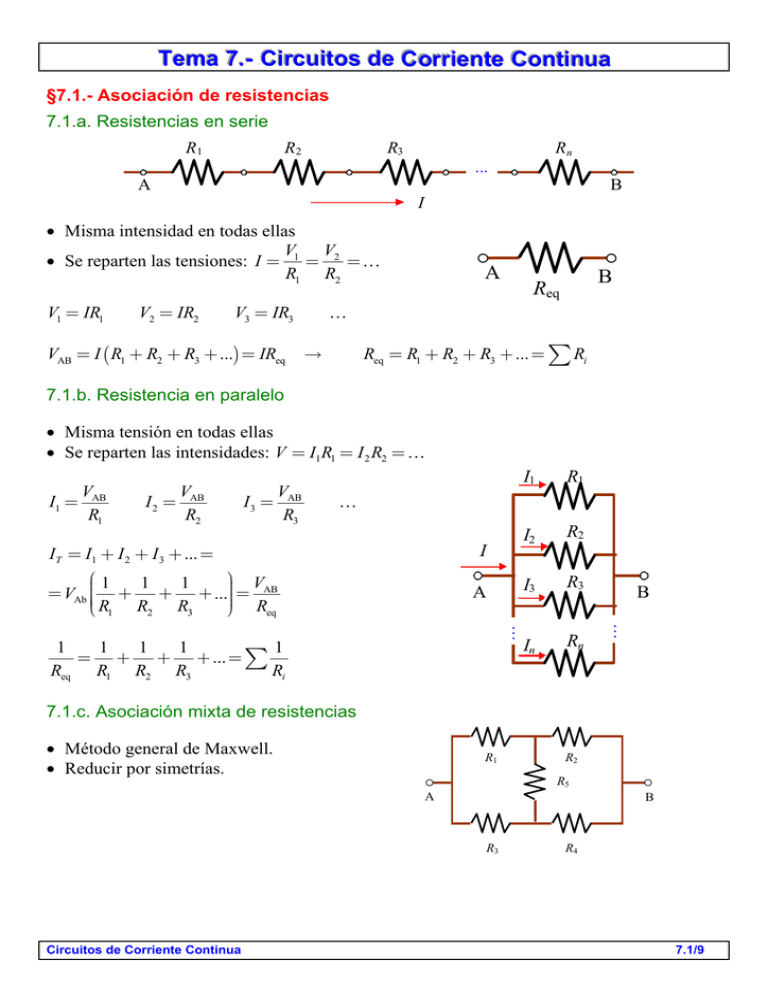
TTeem
Ciirrccuuiittooss ddee C
maa 77..-- C
Coorrrriieennttee C
Coonnttiinnuuaa
0B
§7.1.- Asociación de resistencias
7.1.a. Resistencias en serie
R1
R2
R3
Rn

A
B
I
 Misma intensidad en todas ellas
V
V
 Se reparten las tensiones: I = 1 = 2 =
R1 R2
V1 = IR1
V2 = IR2
V3 = IR3
VAB = I ( R1 + R2 + R3 + ...) = IReq
A
B
Req

Req = R1 + R2 + R3 + ... = å Ri

7.1.b. Resistencia en paralelo
 Misma tensión en todas ellas
 Se reparten las intensidades: V = I1R1 = I 2 R2 = 
V
I1 = AB
R1
V
I 2 = AB
R2
V
I 3 = AB
R3
I1
R1
I2
R2
I3
R3
In
Rn

I
IT = I1 + I 2 + I 3 + ... =
æ1
ö V
1
1
= VAb çç + + + ...÷÷÷ = AB
çè R
÷ø Req
R2 R3
1
A

1
1
1
1
1
= + + + ... = å
Req R1 R2 R3
Ri
B

7.1.c. Asociación mixta de resistencias
 Método general de Maxwell.
 Reducir por simetrías.
R1
R2
R5
A
B
R3
Circuitos de Corriente Continua
R4
7.1/9
§7.2.- Circuito con varios generadores y resistencias en serie
I=
Σ
ΣR
 suma algebráica de las f.e.m.
 suma de las resistencias
d
1,r1
ïìïV
ïV
En efecto: í
V
ï
ï
ï
ïîV
ab
bc
cd
da
= IR2
= Ir2 + 2
= IR1
= Ir1 - 1
ìïV = I (r + r + R + R ) + 
ïï
 -
Σ
í
ïï I =
=
ïî r + r + R + R ΣR
aa

1
2
1
1
2
1
2
2
- 1 = 0
I
a
c
R2
23
1
R1
b
2,r2
2
§7.3.- Fuente de tensión y fuente de intensidad
7.3.a. Fuente de tensión
Elemento activo del circuito capaz de mantener una diferencia de
potencial entre sus terminales.
I=

R+r

VAB = IR =
R

R+r
+
r

B
A
I
I
(*)
R
7.3.b. Fuente de Intensidad
Elemento activo que suministra una intensidad constante al circuito
I = Ic - Ir = Ic I=
r
Ic
R+r
æ
Rö
I c = çç1 + ÷÷÷ I
çè
rø
V
IR
= Ic 
r
r
 VAB = IR =
Ic
Ir
A
(*)
r
R

RI c =
R+r
R+r
\ rI c = 
I
r
V
B
R
Una fuente de tensión será equivalente a una determinada fuente de intensidad cuando al
conectarlas al mismo resistor R suministren igual intensidad.
I=
I r

= c
R+r R+r
 Ic =

r
Ic =

A

r
r
r
B
A
Circuitos de Corriente Continua
(intensidad en corto)
B
7.2/9
§7.4.- Asociación de generadores
7.4.a. Generadores en serie
 Por todos ellos circula la misma intensidad
 Generador equivalente:
1
2
1 ,r 1
VAB = -I (r1 + r2 ... + rn ) - (-1-2 ... - n ) =
I
...
3
B
 n,rn
I
= (1 +2 ... + n ) - I (r1 + r2 ... + rn ) = eq - Ireq
ìïeq = 1 + 2 ... + n = å i
\ íï
ïï req = r1 + r2 + ... + rn = å ri
ïî
n
2 ,r 2
R
I
A
B
eq
req
A
Si todos son iguales: eq = n
B
req = nr
7.4.b. Generadores en paralelo
 La diferencia de potencial en bornes es la misma en todos ellos.
 Sustituimos las fuentes de tensión por las fuentes de intensidad equivalentes:
r1
1
I1
2
r1
r2
B
req
r2
I
I
B
B
A
eq
Icn
rn
n
A
Ic2
I2
A
Ieq
Ic1
req
B
A
rn
In
I eq = å I c,i =
eq
1 2 3

+ + + = å i =
r1 r2
r3
ri
req
 Si todos son iguales: eq = 
req =
ìïeq = I eq req
ïï
 \ ïí 1
1 1 1
1
ïï = + + +  = å
ri
ïïî req r1 r2 r3
r
n
1
2
r1
r2
7.4.c. Asociación mixta de generadores
 Método general de Maxwell.
 Reducir por simetrías.
Circuitos de Corriente Continua
5
A
B
r5
3
r3
4
r4
7.3/9
§7.5.- Lemas de Kirchhoff
 Nudo (n): punto de concurrencia de tres o más elementos
del circuito, tales como los puntos A, B, C, D,...
 Rama (r): elementos comprendidos entre dos nudos
sucesivos. Todos los elemento de la rama están recorridos
por la misma intensidad (intensidad de rama, i).
 Malla (m): circuito cerrado que se puede recorrer sin
pasar dos veces por un mismo nudo.
 Número de mallas independientes: m = r - (n -1)
1
R1
C
2
R2
4
R4
5
R5
3
R3
A
B
D
6
R6
A. Lema de los nudos:
La suma de las intensidades que entran en un nudo es igual a la suma de las que salen de él
(condición de continuidad); i.e., la intensidad neta en un nudo es nula
åi
j
=0
B. Lema de la mallas:
La suma algebraica de las f.e.m.’s en una malla es igual a la suma de los productos de cada
resistencia por la intensidad que la recorre:
VAB = å iR - å 
 VAA = å iR - å  = 0 
å  = å iR
Los lemas de Kirchhoff se aplican a (n - 1) nudos y a m = r - (n - 1) mallas, con lo que
dispondremos de (n - 1) + r - (n - 1) = r ecuaciones con r incógnitas (v.g., las r intensidades
de rama).
Circuitos de Corriente Continua
7.4/9
1,r1
§7.6.- Teorema de superposición
R1
i1
La intensidad de corriente que circula por una rama cualquiera de
un circuito es igual a la suma de las que circularían actuando por sí
solas cada una de las f.e.m.’s presentes en el circuito.
3,r3
A
R3
B
I3
Considerar los efectos de cada fuente de manera independiente
I2
requiere que las fuentes se retiren sin afectar al resultado final. Para
retirar una fuente de tensión al aplicar este teorema, la diferencia de
2,r2
R2
potencial entre los bornes de la fuente de tensión debe ajustarse a
cero; las resistencias internas asociada a las fuentes retiradas no se eliminan, sino que todavía
deberá considerarse.
Ejemplo demostrativo: Aplicamos los lemas de Kirchhoff a (n - 1) nudos y a m = r - (n - 1)
mallas en el circuito que se muestra en la figura.
ìïn = 2
ï
ï
ír = 3
ïï
ïï
îm = 2
ìïi1 + i2 + i3 = 0
ï
ïíïi (r + R ) - i (r + R ) =  - 
1
3 3
3
1
3
ïï 1 1
ïïîi3 (r3 + R3 ) - i2 (r2 + R2 ) = 3 - 2
ì
ïïi1 + i2 + i3 = 0
ï
 ï
íi1 R1 - i3 R3 = 1 - 3
ï
ïïï-i2 R2 + i3 R3 = 3 - 2
î
æ1
1
1 ö÷æ i1 ö æ 0 ö
æ0ö÷
æ 0 ÷ö
æ 0 ÷ö
çç
÷
÷
ç
ç
ç
ç
ç
÷
÷
÷
÷
÷
0 -R3 ÷÷ççi2 ÷÷ = çç 1 - 3 ÷÷   = çç1÷÷1 + çç 0 ÷÷2 + çç-1÷÷÷3 = 1 + 2 + 3
çç R1
֍
ç
çè0ø÷
çè-1÷ø
èç 1 ÷ø
èç 0 -R2 R3 ø÷èçi3 ø÷ èç3 - 2 ÷ø
 =  1 +  2 +  3
-1
-1
1,r1
-1
æ ö æ i ¢ö æ i ¢¢ö æ i ¢¢¢ö
çç i1 ÷÷ çç 1¢ ÷÷ çç 1¢¢÷÷ çç 1¢¢¢÷÷
 çi2 ÷÷ = çi2 ÷÷ + çi2 ÷÷ + çi2 ÷÷
ççèi ø÷ ççi ¢ ÷÷ ççi ¢¢÷÷ ççi ¢¢¢÷÷
è 3ø è 3ø è 3ø
3
R1
i 1’
r1
i1’’
r3
A
R1
r1
B
i3 ’
i 2’
i1’’’
r3
R3
A
R2
 3,r3
R3
B
i 3’’
A
R3
B
i3 ’’’
i2’’’
i2’’
r2
R1
r2
R2
r2
R2
El principio de la superposición no es aplicable a efectos de la potencia, puesto que la
potencia disipada en un resistor depende del cuadrado de la corriente o de la tensión (no
lineal). La potencia total en un elemento se determinará tras haber establecido la corriente
total (o la tensión) a través del elemento mediante la superposición de corrientes (o de
tensiones).
Circuitos de Corriente Continua
7.5/9
§7.7.- Método de las mallas o de Maxwell
1,r1
Asignamos a cada malla una intensidad de malla ( Ii ) de sentido
arbitrario.
ìn = 2
ï
ï
ìïï1 - 3 = I1 (r1 + R1 ) + ( I1 - I 2 )(r3 + R3 )
ï
r
=

3
í
í
ï
ï
I
r
R
I
I
r
R
=
+
+
+
(
)
(
)(
)


2
2 2
2
2
1
3
3
ï
îï 3
ï
ï
îm = 2
ì1 - 3 = I1 (r1 + R1 + r3 + R3 ) - I 2 (r3 + R3 )
ï

íï
ï
ï
î3 - 2 = -I1 (r3 + R3 ) + I 2 (r2 + R2 + r3 + R3 )
R1
i1
I1
3,r3
A
R3
B
i3
I2
i2
2,r2
R2
ì
ï(1) = R11I1 - R12 I 2
æ ö æ R
 R12 öæ
ï
÷çç I1 ÷ö÷   =    = -1
 çç (1) ÷÷÷ = çç 11
í
÷
ç
è R21 R22 øè I 2 ø
ï
ï
î(2) = -R21I1 + R22 I 2 è (2) ø
Notación:
 (i) - f.e.m. neta de la malla i-ésima;
 Ii - intensidad de malla i-ésima;
 Rii - resistencia de la malla i-ésima;
 Ri j - resistencia común a las mallas i-ésima y j-ésima.
o El signo de Rij es negativo si Ii y Ij se restan;
o El signo de Rij es positivo si Ii y Ij se suman.
El método de Maxwell nos proporciona m (< r) ecuaciones con m incógnitas (v.g., las m
intensidades de malla).
A partir de las m intensidades de malla, determinaremos las r intensidades de rama; así, en el
circuito de la ilustración, serán:
i1 = I1
i2 = -I 2
i3 = I 2 - I1
Circuitos de Corriente Continua
7.6/9
§7.8.- Casos prácticos de aplicación del método de Maxwell
7.8.a. Cálculo de la resistencia equivalente
Añadimos un generador arbitrario y calculamos la
intensidad que proporciona al circuito.
R1
A
I2
æ ÷ö æ R11  R1n öæ
÷÷ç I1 ö÷÷
çç ÷ çç
  ÷çç  ÷
ç÷=ç
çè 0 ø÷÷ çèç Rn1  Rnn ø÷÷çèç I n ø÷÷
I1 =
D11

=
D
Req

Req =
R2
R5
B
I3
R3
R4
I1
D
D11

7.8.b. Cálculo de la f.e.m. equivalente (Método de Thévenin)
Abierto: El valor de la f.e.m. equivalente coincide con el de
la d.d.p. entre A y B en circuito abierto. Resolvemos el
circuito para calcular las intensidades de malla I1, I2,...
1
5
I1
A
r2
2
r1
I2
B
r5
æ (1) ö÷ æ R11 -R12 öæ I1 ö
ï I1 = 
ïì
çç ÷ = ç
÷
÷
ç

í
÷
÷
ç
ç
èç(2) ø÷ è-R21 R22 øè I 2 ø
ï
îï I 2 = 
y determinamos VAB en la forma habitual:
3
eq = VAB = å IR - å 
æ(c) ÷ö æ R
çç ÷ ç cc -Rc1 -Rc2 ö÷çæ I c ö÷÷
çç (1) ÷÷ = çç-R1c R11 -R12 ÷÷÷çç I1¢÷÷  I c = 
÷ç ÷
ç ÷ ç
èç(2) ÷ø èç-R2c -R21 R22 øçè I 2¢ ø
y la resistencia interna del generador equivalente entre A y B
será:
eq
req

req =
eq
Ic
r4
eq
En corto: Cortocircuitamos entre A y B y determinamos la
intensidad en corto (Ic) que puede proporcionar el circuito
entre A y B:
Ic =
4
r3
req
A
1
2
r1
5
I’1
A
B
r2
I’ 2
B
r5
3
r3
4
r4
Ic
A
eq
req
B
Ic
Aclaración: La req también puede calcularse mediante el procedimiento descrito en 7.8.a,
sin más que cortocircuitar (ignorar) todas las f.e.m (manteniendo las resistencias internas de
los generadores).
0H
Circuitos de Corriente Continua
7.7/9
§7.9.- Circuito RC en C.C.
7.9.a. Carga de un condensador

En el instante inicial el conmutador (S) está en la posición inferior
y el condensador está descargado. Al conectar el generador
(t = 0), comienza a circular la carga.
 = V = vR + vC = Ri +
i=
V
q
R RC
di
i
=dt
RC
q
C
S
i
i
R
+
ì
V
ï
+
ï
t
0
q
0
i
I
=
=
=
=
0
ï
R
í
ï
ï
ï
ît = ¥ q = Qf = CV i = 0
i (t )

ò
I0
t
di
dt
= -ò
i
RC
0
 ln
i
t
=I0
RC
C
q

i (t ) = I 0e-t / RC
Constante de tiempo: t = RC ; para t = t  i (t ) = I 0e-1 = I 0 / e = 0.37 I 0
τ es el tiempo que transcurre en el proceso de carga hasta que la corriente se reduce al 37%
de su valor máximo inicial.
q (t )
t
dq
= i = I 0e-t / RC  ò dq = I 0 ò e-t / RC dt 
0
0
dt
t
q (t ) = I 0 éëê-RCe-t / RC ùûú = I 0 RC (1 - e-t / RC ) = C (1 - e-t / RC ) = Qf (1 - e-t / RC )
0
τ es el tiempo que transcurre en el proceso de carga hasta que el condensador adquiere el
63% de su carga máxima.
q i
Qf
I0
q(t ) = Qf (1 - e-t / RC )
0.63Qf
0.37I0
i (t ) = I 0e-t / RC
τ
Circuitos de Corriente Continua
t
7.8/9
7.9.b. Descarga de un condensador
El condensador está inicialmente cargado con una carga Q0. En
el instante t = 0 se pasa el conmutador a la posición inferior,
iniciándose la descarga a través de la resistencia.
Vab = vR + vC = iR +
q
i =RC
di
i
=dt
RC

ò
I0
S
q
=0
C
i
ìï
ïït = 0+ q = Q0
í
ïï
ïît = ¥ q = 0
i (t )

i = I0 = -
Q
RC
R
a
i=0
t
di
dt
= -ò
i
RC
0
 ln
i
t
=I0
RC

C
+
c
b
i (t ) = I 0e-t / RC
Constante de tiempo: t = RC ; para t = t  i (t ) = I 0e-1 = I 0 / e = 0.37 I 0
τ es el tiempo que transcurre en el proceso de descarga hasta que la corriente se reduce al
37% de su valor máximo inicial.
i=
q ( t ) dq
t
dq
q
1
dt 
= ò
=Q0
dt
RC
q
RC ò0
q (t )
t
ln
= q (t ) = Q0e-t / RC
Q0
RC
τ es el tiempo que transcurre en el proceso de descarga hasta que el condensador reduce su
carga hasta el 37 % de su carga inicial.
q i
Q0
q (t ) = Q0 e-t / RC
0.37Q0
τ
t
-0.37I0
i(t ) = I 0e-t / RC
-I 0
Circuitos de Corriente Continua
7.9/9