Page 1 Fundamentos Físicos de la Ingeniería Examen
Anuncio
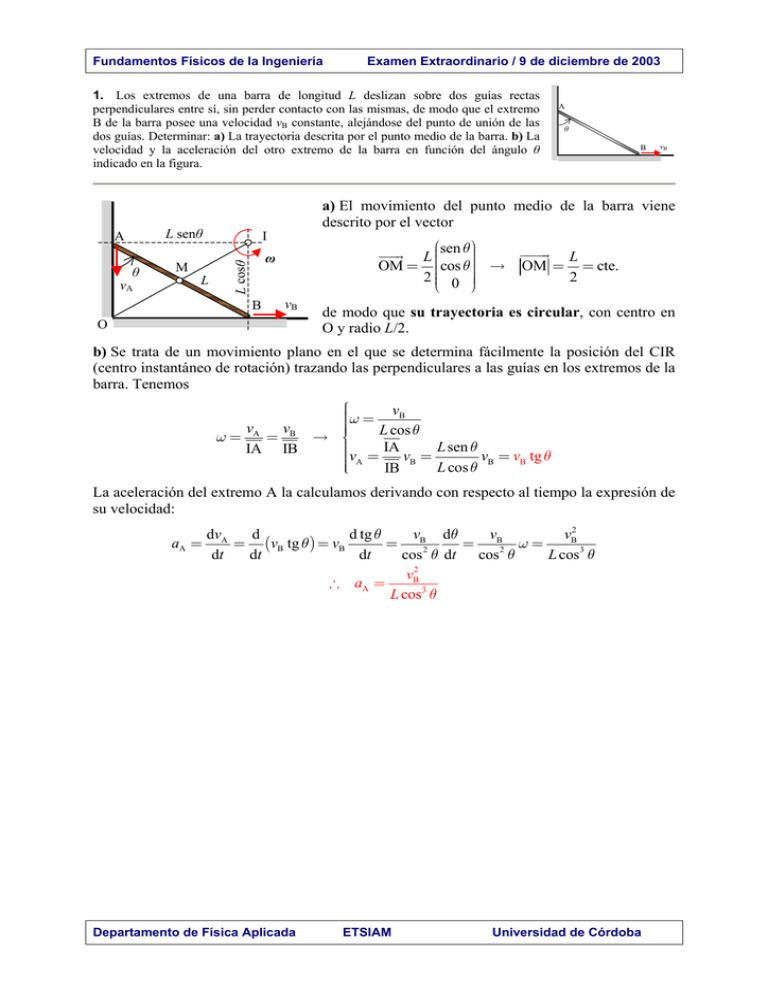
Fundamentos Físicos de la Ingeniería Examen Extraordinario / 9 de diciembre de 2003 1. Los extremos de una barra de longitud L deslizan sobre dos guías rectas perpendiculares entre sí, sin perder contacto con las mismas, de modo que el extremo B de la barra posee una velocidad vB constante, alejándose del punto de unión de las dos guías. Determinar: a) La trayectoria descrita por el punto medio de la barra. b) La velocidad y la aceleración del otro extremo de la barra en función del ángulo θ indicado en la figura. L senθ θ vA M L B vB !!!!" L !!!" L sen θ OM = cos θ → OM = = cte. 2 0 2 ω B θ a) El movimiento del punto medio de la barra viene descrito por el vector I L cosθ A A vB O de modo que su trayectoria es circular, con centro en O y radio L/2. b) Se trata de un movimiento plano en el que se determina fácilmente la posición del CIR (centro instantáneo de rotación) trazando las perpendiculares a las guías en los extremos de la barra. Tenemos vB ω = v v L cos θ ω= A = B → IA IB v = IA v = L sen θ v = v tg θ B A IB B L cos θ B La aceleración del extremo A la calculamos derivando con respecto al tiempo la expresión de su velocidad: dvA vB dθ vB vB2 d d tg θ aA = = (vB tg θ ) = vB = = ω= dt dt dt cos 2 θ dt cos 2 θ L cos3 θ vB2 ∴ aA = L cos3 θ Departamento de Física Aplicada ETSIAM Universidad de Córdoba Fundamentos Físicos de la Ingeniería Examen Extraordinario / 9 de diciembre de 2003 2. Una placa rectangular y homogénea, de dimensiones 30 cm x 20 cm, pesa 2 kg y está unida a un eje vertical de modo que en A está articulada con el eje y en B tan solo se apoya en él, como se indica en la figura. a) Determinar las reacciones en A y en B cuando el sistema está en rotación con una velocidad angular de 30 r.p.m. b) ¿A partir de que valor de la velocidad angular no se apoyará en B? Reconducimos el problema a un problema de estática (equilibrio estático) analizándolo en un referencial en rotación en el que la placa se encuentra en reposo. En estas condiciones, el diagrama de fuerzas es el que se muestra en la figura, incluida la fuerza centrífuga. Cálculo de la fuerza centrífuga: Sea un elemento de masa dm = σbdx , de modo que a 1 1 1 dFcf = (ω 2 x) dm = ω 2σbx dx → Fcf = ω 2σb ∫ x dx = ω 2σba 2 = ω 2 (σba ) a = maω 2 0 2 2 2 a) Escribimos las ecuaciones cardinales de la estática, tomando momentos en A: → [1] RA = P RA NA ↑ [2] N B + Fcf = N A dx a=30 cm b a Fcf + bN B = P 2 2 Fcf G C de modo que disponemos de tres ecuaciones con tres incógnitas (NA, NB y RA) b=20 cm ! [3] A NB B De la primera, se sigue que RA = P P x De la tercera, obtenemos NB = ma 1 1 1 bω 2 2 aP − bF = mga − m ω ab = g − ( cf ) 2b 2b 2b 2 2 y sustituyendo en la segunda ecuación N A = N B + Fcf = mga 1 1 mga 1 ma bω 2 − maω 2 + maω 2 = + maω 2 = g + 2b 4 2 2b 4 2b 2 b) Para una cierta velocidad angular crítica, ωcrít, desaparece la ligadura en B (i.e., NB=0): NB = 2 2 bωcrít bωcrít ma 2g g − 0 → g − = 0 → ωcrít = 2b 2 2 b Sustituyendo los valores dados, RA = 2 kg = 19.6 N 2×0.30 0.20×π 2 = 16.2 N = 1.65 kg N 9.8 = + a 0.30 m = A 2×0.20 2 b = 0.20 m 2 → N B = 2×0.30 9.8 − 0.20×π = 13.2 N = 1.35 kg m 2 kg = 2×0.20 2 ω = 30 r.p.m. = π rad/s ω = 2×9.8 = 9.9 rad/s = 94.5 r.p.m. crít 0.2 Departamento de Física Aplicada ETSIAM Universidad de Córdoba Fundamentos Físicos de la Ingeniería Examen Extraordinario / 9 de diciembre de 2003 3. La barra homogénea de la figura puede girar sin rozamiento alrededor de un eje horizontal que pasa por uno de sus extremos. Se coloca en posición horizontal y se abandona. Determinar: a) La aceleración angular de la barra en el instante en que se deja en libertad. b) La fuerza ejercida por el eje sobre la barra en ese instante. c) La velocidad del centro de masa de la barra cuando ésta alcanza la posición vertical. m, L a) Aplicamos la ecuación fundamental de la dinámica de rotación, tomando momentos con respecto al eje de rotación: mg L 1 3g = I α = mL2α → α = 2 3 2L b) El c.m. de la barra describe una trayectoria circular, de radio L/2, de modo que las componentes intrínsecas de su aceleración, en el momento inicial, son + + Ny Nx m, L + L 3 at = α = g 2 4 v2 an = =0 L/2 Aplicando las ecuaciones del movimiento del c.m, tenemos: N x = man = 0 N x = 0 → 3 mg − N y = mat = mg N y = 1 mg 4 4 mg c) Puesto que el sistema es conservativo, y solo estamos interesados en la velocidad final, nos serviremos del Principio de Conservación de la Energía para determinar la velocidad angular de la barra en el instante pedido: ω Ep=0 0 = −mg L 1 2 + Iω 2 2 L/2 vcm → ω2 = mgL mgL 3g = = 1 I L mL2 3 y la velocidad de su centro de masa, en ese instante, será: vcm = ω Departamento de Física Aplicada ETSIAM L L 3g 1 3 gL = = 2 2 L 2 Universidad de Córdoba Fundamentos Físicos de la Ingeniería Examen Extraordinario / 9 de diciembre de 2003 4. Un bloque de masa m se deja caer desde una altura h sobre un muelle de constante elástica k. Determínese el acortamiento del muelle justamente antes de iniciarse la subida de la masa. Dado que el sistema es conservativo, aplicamos el Principio de Conservación de la Energía. Tanto en el instante inicial como en el de máximo acortamiento del muelle son nulas la energía cinética, ya que el bloque se encuentra instantáneamente en reposo, de modo que tiene lugar una conversión de energía potencial gravitatoria en elástica; esto es, 1 mgh = −mgx + kx 2 2 → kx 2 − 2mgx − 2mgh = 0 Resolvemos la ec. cuadrática, m x2 mg + 2h mg > 0 k k mg − k mg + 2h mg < 0 k k m x1 2 mg x1 = + k m + h Ep,grav=0 de modo que tenemos dos soluciones x2 = En reposo k k En reposo mg ± m 2 g 2 + 2kmgh x= k 2 una positiva y otra negativa, que corresponden a los instantes en los que el bloque se encuentra instantáneamente en reposo, tal como se indica en la figura. Puesto que nos piden el máximo acortamiento del muelle, éste será mg x1 = + k • 2 mg mg >0 + 2h k k Obsérvese que el acortamiento del muelle correspondiente a la posición de equilibrio, con el bloque encima mg de él, vale x0 = , y que la amplitud de las oscilaciones del sistema, en el caso de que el bloque quede k 2 mg mg unido al muelle, vale A = + 2h k k • Caso particular: Si fuese h = 0, sería: x1 = Departamento de Física Aplicada 2mg k ETSIAM x2 = 0 x0 = mg k A= mg k Universidad de Córdoba Fundamentos Físicos de la Ingeniería Examen Extraordinario / 9 de diciembre de 2003 5. Por una tubería circula un caudal de 208 L/s de agua. En la tubería se ha instalado un medidor de Venturi, con mercurio en su interior, tal como se representa en la figura. Si las secciones de la tubería en 1 y 2 son 800 y 400 cm2, respectivamente, calcular el desnivel h que se produce en el mercurio. 1 2 h Aplicamos la ec. de Bernoulli entre 1 y 2: 1 1 p1 + ρv12 = p2 + ρv22 2 2 → 1 p1 − p2 = ρ (v22 − v12 ) 2 [1] Aplicamos reiteradamente la ec. hidrostática en el camino 1AB2: (1 → A) → p1 + ρ gz1 = pA + ρ gzA (A → B) → pA + ρm gzA = pB + ρm gzB ( B → 2) → pB + ρ gzB = p2 + ρ gz2 1 ρ y sumando m.a.m. A p1 + ρm gzA + ρ gzB = ρ gzA + ρm gzB + p2 → p1 − p2 = (ρm − ρ ) g ( zB − zA ) = (ρm − ρ ) gh 2 h B ρm [2] Igualamos las ecuaciones [1] y [2] 1 ρ v22 − v12 2 2 (ρm − ρ ) gh = ρ (v2 − v1 ) → h = 2 ρm − ρ 2 g [3] Aplicamos las ecuación de continuidad entre los puntos 1 y 2: C = v1S1 = v2 S 2 → v1 = C S1 v2 = C S2 [4] y sustituyendo las velocidades en la ec. [3]: 2 2 ρ C C 1 ρ 1 1 C 2 − − = h= ρm − ρ S 2 S1 2 g ρm − ρ S 22 S12 2 g Aplicación numérica: h= 1 1000 1 0.2082 − = 0.082 m = 82 mm 13600 −1000 0.042 0.082 2×9.8 Departamento de Física Aplicada ETSIAM Universidad de Córdoba Fundamentos Físicos de la Ingeniería Examen Extraordinario / 9 de diciembre de 2003 6. Una botella de acero, cerrada y de volumen constante, contiene en su interior 0.5 kg de oxígeno a la presión de 10 atm y temperatura de 20 ºC. Hállense: a) La capacidad de la botella de acero. b) La presión que se alcanzará en su interior, cuando se calienta el oxígeno hasta 80 ºC . c) El incremento de entropía del oxígeno al realizarse el calentamiento descrito en el apartado b). 500 = 15.625 mol y, puesto que se trata 32 5 de un gas (ideal) biatómico, será CV = R . 2 0.5 kg de oxígeno representan a) Determinamos el volumen ocupado por el gas (capacidad de la botella) a partir de la ec. de estado de los gases perfectos: p1V = nRT1 → V = p2 p1 V nRT1 15.625× 0.08206× 293 = = 37.57 L p1 10 b) Cuando lo calentamos a volumen constante hasta 80 ºC = 353 K, la presión aumenta: p1 p = 2 T1 T2 → p2 = T2 353 p1 = ×10 = 12.05 atm T1 293 c) En el proceso isocoro (a volumen constante) el incremento de entropía será ∆S = ∫ T2 đQ dT T 5 353 cal = nCV ∫ = nCV ln 2 = 15.625× ×1.987 × ln = 14.46 T T T1 2 293 K T 1 Departamento de Física Aplicada ETSIAM Universidad de Córdoba Fundamentos Físicos de la Ingeniería Examen Extraordinario / 9 de diciembre de 2003 7. Disponemos de dos condensadores, de capacidades C1 y C2, que han sido cargados, por separado, a las tensiones V1 y V2 respectivas, siendo V1 ≠ V2. Los conectamos en paralelo, uniendo los bornes de igual polaridad. a) Demostrar que la energía electrostática almacenada en este montaje es inferior a la energía total cuando los condensadores estaban separados. b) ¿Por qué ocurre esto? a) Energía electrostática total almacenada en los condensadores separados: Q1=C1V1 + U= + 1 C1V12 + C2V22 ) ( 2 Capacidad del condensador equivalente al montaje en paralelo: Q2=C2V2 Ceq = C1 + C2 + La carga neta almacenada en los condensadores permanece constante al unirlos en paralelo: + Q1 + Q2 = C1V1 + C2V2 C V + C2V2 V= 1 1 Q1′ + Q2′ = (C1 + C2 )V C1 + C2 Q’1=C1V Q’2=C2V Energía electrostática total almacenada en los condensadores montados en paralelo: + 2 1 1 (C1V1 + C2V2 ) U ′ = CeqV 2 = 2 2 C1 + C2 Q=CeqV Variación de la energía almacenada 1 C 2V 2 + C22V22 + 2C1C2V1V2 C12V12 + C1C2V22 + C1C2V12 + C22V22 = ∆U = U ′ −U = 1 1 − 2 C1 + C2 C1 + C2 = 1 C1C2 1 C1C2 2 2V1V2 −V12 −V22 ) = − (V1 −V2 ) < 0 ( 2 C1 + C2 2 C1 + C2 de modo que la energía electrostática disminuye. b) La energía electrostática disminuye debido a que, durante la conexión de los condensadores, pasa carga de un condensador a otro, estableciéndose una corriente eléctrica a través de los hilos de conexión, desprendiéndose calor en ellos. La cantidad de calor desprendida no depende de la resistencia de los hilos de conexión; si éstos presentan una resistencia pequeña, la intensidad de la corriente será grande e inversamente. Obsérvese que si fuese V1 = V2, sería ∆U = 0; y que si C1 = C2 y V2 = 0, sería U’=U/2 Departamento de Física Aplicada ETSIAM Universidad de Córdoba Fundamentos Físicos de la Ingeniería Examen Extraordinario / 9 de diciembre de 2003 A 8. Determinar la resistencia equivalente entre los puntos A y B del circuito representado en la figura. 3Ω 2Ω 6Ω 6Ω Suministramos corriente al circuito conectando un generador de f.e.m. entre los nudos A y B y resolvemos el circuito por el método de las mallas de Maxwell: Tan sólo estamos interesados en la intensidad de corriente suministrada por el generador externo, ya que I2 Departamento de Física Aplicada ETSIAM 6Ω 2Ω I3 E I1 B 6Ω A nos permite calcular la resistencia equivalente entre A y B: E ∆ 348 348 = = = = 2.95 Ω 11 −6 118 I1 ∆11 −6 14 3Ω 2Ω E −2 − 6 ∆ 1 I1 = 0 11 −6 = 11 E ∆ ∆ 0 −6 14 RAB = B A E ! 8 −2 −6 I1 # 0 = −2 11 −6 I 2 → ∆ = 348 Ω3 I 0 −6 −6 14 3 2Ω RAB E I1 B Universidad de Córdoba Fundamentos Físicos de la Ingeniería Examen Extraordinario / 9 de diciembre de 2003 9. Un conductor rectilíneo indefinido y una espira cuadrada están situados en un mismo plano. La espira, de lado a, tiene el lado más cercano al conductor paralelo al mismo y a una distancia igual a su lado. Determínese la fuerza electromotriz inducida en la espira cuando por el conductor rectilíneo circula una corriente i = I sen ωt . i a a El teorema de Ampère nos permite determinar la intensidad del campo magnético a una distancia r de un largo conductor rectilíneo que transporta una intensidad de corriente i. Para ello, calculamos la circulación de campo B a lo largo de una trayectoria circular (línea de campo) situada en un plano perpendicular al conductor: i r B ∫$ Bidl = ∫$ Bdl = B ∫$ dl = B 2πr = µ i 0 → B= µ0 i 2π r El campo magnético es perpendicular al plano de la espira, su sentido es hacia adentro y su magnitud decrece con la distancia al hilo rectilíneo conductor. i × × × × × × × a× × × × r× × × × × × × × × × × × × × × × × × × × dr× a× × × × × × × × Calculamos el flujo a través de una franja estrecha, de espesor dr, de superficie dS = adr, situada a una distancia r del hilo. × × × × × × × × × × × a×× × × × dΦ=B ⋅ dS = B dS = µ0 i µ dr a dr = 0 ia 2π r 2π r e integramos sobre toda la superficie de la espira, 2a µ µ0 dr µ0 Φ= = ia ∫ ia ln 2 = 0 Ia ln 2 sen ωt 2π 2π a r 2π De acuerdo con la ley de Faraday, la f.e.m. inducida en la espira es E =− µ d µ dΦ = − 0 Ia ln 2 sen ωt = − 0 I ω a ln 2 cos ωt 2π 2π dt dt Departamento de Física Aplicada ETSIAM Universidad de Córdoba



