IDENTIFICACIÓN DE DATOS: MEDICIÓN
Anuncio

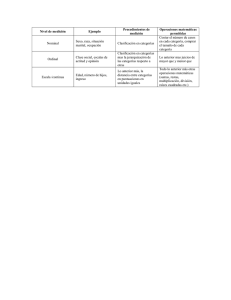
Tema 4 IDENTIFICACIÓN DE DATOS: MEDICIÓN pp. 109-123 1. Identificación de datos para la selección C Datos Cxto Cxto Selección basada en datos obtenidos, identificados en contextos específicos CCtx ≈ Datos Ctx Recuerda, l l l Identificación: CCtx ≈ DatosCtx ¿Qué hacemos cuando identificamos datos? ¿Qué hay de semejante al responder los tres casos siguientes? • ¿De qué color es la pared? • ¿Cuántos estamos aquí? • ¿Hay alguien con una prenda de vestir roja? INTENTA APLICAR LO VISTO DE SELECCIÓN BASADA EN DATOS 1. Identificación de datos 1.1. Noción ampliada y casos -”Identificar”: -”Identificar”: Considerar Considerar algo algo idéntico idéntico aa una una referencia referencia En Enparticular, particular,identificación identificaciónde dedatos datos ooevidencias: evidencias: constatación constatación de de una una correspondencia correspondencia de de semejanza semejanza entre entre valores valores de de un un concepto concepto de de referencia referencia yy datos, datos, ambos ambos en en contextos contextos similares. similares. C ˜ Datos Cxto1 ˜ Cxto1 1.2. Notas: sobre la noción l Identificar supone: • Recoger de datos • Aportar significado a lo identificado • (éste no lo tiene por sí mismo) 1.2. Notas: otras implicaciones (I) ¿Qué es esto? ¿Qué dato podemos recoger de esto? 1.2. Notas: otras implicaciones (II) Puesto que Identificación implica l CCtx ≈ Datos Ctx Los datos obtenidos – y sus dimensiones- varían según: • las del concepto de referencia • Sin conceptos de referencia no hay identificaciones • las del contexto de referencia • otros supuestos y conceptos implícitos Expresándolo gráficamente : Otros Modelo Datos Cxto Cxto ...y simbólicamente: Datos = f ( modelo de referencia + contexto + otros factores implícitos) 1.2. Notas: otras implicaciones Ya que Datos = f ( modelo de referencia + contexto + otros factores implícitos) l ¿Se puede recoger datos sin concepto de referencia? • ¿Hablan los datos “por sí mismos”, al margen de todo concepto de referencia? l El concepto de referencia es planteados por personas • Todo conocimiento es subjetivo l ¿Cómo concebir entonces la objetividad? • ¿Conocimiento sin influencia de ningún concepto de referencia? Objetividad: Objetividad:Subjetividad Subjetividadcompartida compartida Datos Datosobjetivos: objetivos:Obtenidos Obtenidosdesde desdeyysegún segúnun un determinado determinadoconcepto conceptode dereferencia referencia TIPOS DEL CONCEPTO USADO COMO REFERENCIA PARA LA IDENTIFICACIÓN Distinguir tipos en los siguientes casos Género Mujer Acuerdo Hombre con un tema Habitaciones de vivienda Baño Líneas autobuses Centro - 1 Poco –1 Norte - 2 Este - 3 Algo –2 Oeste - 4 Sur - 5 Cocina Comedor Estar Dormitorios Género Mucho – 3 Mujer - 1 Hombre - 0 0 10 20 30 pp. 123-140 2. Medición 2.1. Nociones ampliadas y casos Dimensiones Formas de expresión Casos de Identificación Basadas en conceptos verbales o sistemas de categorías o taxonomías. Basadas en conceptos verbales –o icónicos- y además numéricos (escalas). Ejemplo de sistema de categorías para evaluar el estrés psicosocial. DSM Categoría Ejemplos de muestra en el adulto Ninguno No hay estrés aparente Mínimo Violación menor de la ley. Pequeño préstamo del banco Leve Discusión con el vecino. Cambio de horario de trabajo. Moderado Nueva carrera. Muerte de un amigo. Embarazo. Intenso Enfermedad grave del individuo o de un familiar. Pérdida de una cantidad importante de dinero. Separación conyugal. Nacimiento de un hijo. Extremo Muerte de un pariente cercano. Divorcio. Catastrófico No especificado Experiencia de campo de concentración. Desastre natural devastador. Falta de información o información no utilizable. Escala: Correspondencia sistema empírico (verbal o icónico) y sistema numérico. Algunos ejemplos Sistema empírico “Género” Sistema numérico (x) Hombre 0 Acuerdo SE – SN Poco –1 Algo –2 Mucho – 3 1 Mujer SN SE 0 10 20 30 Escala: correspondencia sistema empírico y sistema numérico Correspondencia unívoca pero no única (varios SN) Sistema empírico “Género” Sistema numérico (x) SN Transformado (x’) Hombre 0 5 211 Correspondencia unívoca Mujer 1 ¿Es posible? 0 19 2 Con transformaciones admisibles: Escalas con unicidad Sobre esa base, Medir: identificar datos basándose en una escala asignar los números que en ella corresponda a los valores de un sistema empírico identificados en contextos específicos. 0 10 20 30 Acuerdo 10,02 Poco –1 Algo –2 Mucho – 3 Poco Poco Poco––11 Poco 2. Medición 2.1. Nociones ampliadas y casos Dimensiones Formas de expresión Casos de Identificación Basadas en conceptos verbales o sistemas de categorías o taxonomías. Basadas en conceptos verbales –o icónicos- y además numéricos –escalas-. Medición Dimensiones Casos de Mediciones Formas de expresión Basadas en conceptos verbales (Sistemas de categorías) y numéricos (Escalas) Especificación *confirmatorias o exploratorias *escalas por extensión o comprensión *escalas a nivel de indicadores Contenido *Referidos a características de sujeto, medio y estudio *También simulación Composición *De variables y relaciones de cualquier tipo *indirectas en muchos casos Valores Basadas en escalas de tipo: *Nominal: sistema empírico cualitativo *Ordinal: sistema empírico ordinal *Intervalo lineal: sistema empírico cuantitativo: *Razón: sistema empírico cuantitativo: (unidad de medida y valor de origen) (ordenar proporciones) Ejemplos de escalas nominales Andalucía – 1 Cataluña -2 Hombres – 1 Galicia – 3 Mujeres - 0 Madrid – 4 Neurosis – 3 Salón – 1 Psicosis – 2 Baño – 2 Psicopatía - 1 Dormitorio - 3 Ejemplos de escalas ordinales Altos – 1 Poco acuerdo – 1 Bajos - 0 Algo de acuerdo -2 Bastante acuerdo – 3 -1 -2 Mucho acuerdo – 4 Clase alta – 3 -3 Clase media – 2 -4 Clase baja - 1 Ejemplos de escala de intervalo Acuerdo con 20 opiniones – 20 Acuerdo con 10 opiniones – 10 Acuerdo con 0 opiniones - 0 Unidad: Una opinión Congelación agua – 0º Medio – 50 º Unidad: Un grado Ebullición - 100 Conocimiento de 40 preguntas – 10 Conocimiento de 20 preguntas – 5 Unidad: Una pregunta Conocimiento de 0 preguntas - 0 Ejemplos de escala de razón l l l l l Longitud del SMD Peso del SMD Longitud del sistema sajón Frecuencia de agresiones físicas Tiempo en medidas sexagesimales Dado que las escalas de intervalo no mantienen proporciones entre valores ¿qué frases tienen sentido y cuáles no? “Hoy “Si hoy -concomo 20º-ayer hacehace el doble 10º, de en calor total que hemos ayer -con estado 10º-” a 20º” “Hoy -con 20º- el mercurio subió desde cero una distancia doble que ayer -con 10º-” “Yo se la mitad que tu, porque saqué 10 preguntas bien y tu 20” “Si me junto con alguien que haya sacado otras 10 preguntas, entre los dos sabremos igual que el que ha sacado 20” “Yo he sacado la mitad de preguntas que tu. Se menos que tu en este examen” Relaciones con sentido empírico en cada medición y escala Escalas Relaciones Nominal Ordinal Intervalo Razón SI SI SI SI SI SI SI =/? SI SI >/< SI SI =/? Valores >/< Distancias Proporcione s =/? SI >/< SI 2.2. Notas: sobre los casos Transformaciones admisibles Con escalas nominales: Son admisibles las transformaciones que mantengan sus criterios definitorios. ESCALA Y MEDICIÓN Nominal Expresado formalmente TRANSFORMACIÓN de SN a SN* (x: valor numérico original) (x’: valor transformado) x’= f(x) siendo f(x): identidad/diferencia Sistema empírico Sistema Numérico x Sistema N*. Transform. x’ Sí 1 1 No 0 2 Ej. transformaciones admisibles escala nominal x’= f(x) f(x): identidad/diferencia Sistema empírico “Género” Sistema numérico (x) SN Transformado (x’) Hombre 0 30 5 1 Mujer 1 50 0 1 5 2 Transformaciones admisibles según el tipo de valores de cada sistema empírico ESCALA Y MEDICIÓN TRANSFORMACIÓN (x: valor numérico original) (x’: valor transformado) Nominal x’= f(x) f(x): identidad/diferencia Ordinal x’= f(x) f(x): monotónica creciente o decreciente Intervalo lineal x’= f(x) f(x) = ax + b Razón x’= f(x) siendo f(x) = ax x’= x’=f(x) f(x) f(x): f(x):monotónica monotónicacreciente crecienteoo Ej. transformación decreciente decreciente S. empírico: “Nivel de estudios” admisible escala ordinal Sistema numérico (x) SN Transformado (x’) N.e. Bajo 1 100 10 3 N.e. Medio 2 300 15 1 N.e. Alto 3 2500 20 2 x’= f(x) Ej. transformación admisible escala f(x) = ax + b intervalo Sistema empírico “Temperatura” Sistema numérico (ºC) SN Transformado (ºF)=1,8ºC+32 Congelación del agua 0º C 32º F Valor medio 50º C 122º F Ebullición del agua 100º C 212ºF Muestra de la transformación admisible de escala centígrada a Farenheit: x’=1,8x + 32 Distancias Comparación temperaturas ºC ºF Proporciones ºC ºF Congelación y punto medio 0-50= 50 32-122 =90 0/50 =0 32/122 =0,3 Medio y ebullición 50-100 = 50 122-212 =90 50/100=0,5 122/212=0,6 Congelación y ebullición 100 180 0/100=0 32/212=0,2 x’= f(x) f(x) transformación = ax Ej. Sistema empírico “Tiempo” admisible en escala razón Sistema numérico (Horas) SN Transformado Minutos=60H Inicio del día 0 horas 0 minutos Mediodía 12 horas 720 minutos Fin del día 24 horas 1440 minutos Ej. transformación admisible escala razón: De escala horaria a minutera x’=60x Distancias Proporciones Comparación Tiempos Horas Minutos Horas Minutos Inicio y medio día 12 720 0/12 = 0 0/720 = 0 Medio y fin del día 12 720 12/24=0,5 720/1440=0,5 Inicio y fin del día 24 1440 0/24 = 0 0/1440 = 0 2.2. Notas: sobre los casos (II) l ‘Escala’: tanto específica como un tipo • “Escala de actitudes hacia la Estadística” • “Escala de tipo ordinal” l Combinables l Progresivamente inclusivos 2.2. Notas: sobre la noción Escalas: l ‘Medición’ ( y ‘medida’): Proceso y resultado l Significado de números dependiente del sistema empírico 2.2. Notas: sobre la noción Escalas: l ‘Medición’ ( y ‘medida’): Proceso y resultado l Números dependientes del sistema empírico • Ventajas de los números: sencillez y operaciones 1.2. Notas: otras implicaciones: Puesto que medición es CRCxto-DatosCxto, las medidas obtenidas en un contexto determinado dependen de... Otros Escalas Medidas Cxto Cxto Datos numéricos = f ( escalas de referencia + contexto + factores implícitos) Resumen del PROGRAMA visto hasta ahora l Conceptos como material de la profesión • Dimensiones l Tareas de la profesión (con conceptos). • Descritas en términos de relaciones entre conceptos Sucesión: Variación – Selección – Variación... c1 Problema Sucesión: Variación – Selección – Variación... c1 Datos cV Variación C1 ≠ Cv Selección Selección Cv ≈ Datos Resumen. Estructura de cada tema l Noción: • l Casos: • l Por comprensión Por extensión Notas • Sobre casos • Sobre noción • Otras implicaciones •Todo •Todoello elloexpuesto expuestocon conconceptos conceptosyyejemplos ejemplos (Constructos (Constructoseeindicadores, indicadores,respectivamente) respectivamente)