Equivalencias e Implicaciones Lógicas TAII(I)
Anuncio

Equivalencias e Implicaciones Lógicas
TAII(I)
Existe un conjunto de equivalencias e implicaciones lógicas que pueden
utilizarse como esquemas de sustitución en procesos de razomamiento, o como
esquemas de razonamientos válidos respectivamente. A continuación se muestra
un breve resumen de las más importantes:
1.
Equivalencias Lógicas
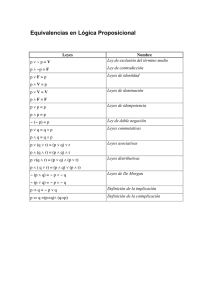
EQUIVALENCIA
P ∨ ¬P ≡ T
P ∧ ¬P ≡ F
P ↔ Q ≡ (P → Q) ∧ (Q → P )
P → Q ≡ ¬P ∨ Q
P → Q ≡ ¬(P ∧ ¬Q)
P ∨F ≡P
P ∧T ≡P
P ∨T ≡T
P ∧F ≡F
P ∨P ≡P
P ∧P ≡P
¬(¬P ) ≡ P
P ∨Q≡Q∨P ; P ∧Q≡Q∧P
(P ∨ Q) ∨ R ≡ P ∨ (Q ∨ R)
(P ∧ Q) ∧ R ≡ P ∧ (Q ∧ R)
(P ∨ Q) ∧ (P ∨ R) ≡ P ∨ (Q ∧ R)
(P ∧ Q) ∨ (P ∧ R) ≡ P ∧ (Q ∨ R)
¬(P ∧ Q) ≡ ¬P ∨ ¬Q
¬(P ∨ Q) ≡ ¬P ∧ ¬Q
NOMBRE
Ley del Tercio Excluido
Principio de No Contradicción
Def. de la doble implicación en función de la implicación
Def. de la implicación en función de la disyunción
Def. de la implicación en función de la conjunción
Leyes de la Identidad
Leyes de Dominación
Leyes de la Idempotencia
Ley de la Doble Negación
Leyes Conmutativas
Leyes Asociativas
Leyes Distributivas
Leyes de De Morgan
1
2.
Implicaciones Lógicas
IMPLICACIÓN
{P, Q} |= P ∧ Q
{P ∧ Q} |= P
{P ∧ Q} |= Q
{P } |= P ∨ Q
{Q} |= P ∨ Q
{P → Q, P } |= Q
{P → Q, ¬Q} |= ¬P
{P → Q, Q → R} |= P → R
{P ∨ Q, ¬P } |= Q
{P ∨ Q, ¬Q} |= P
{P → Q, ¬P → Q} |= Q
{P ↔ Q} |= P → Q
{P ↔ Q} |= Q → P
{P → Q, Q → P } |= P ↔ Q
{P, ¬P } |= Q
NOMBRE
Ley de Combinación
Leyes de Simplificación
Leyes de Adición
Modus Ponens
Modus Tollens
Silogismo Hipotético
Silogismos Disyuntivos
Prueba por casos
Eliminación de la equivalencia
Introducción de la equivalencia
Ley de Inconsistencia
2