MONOPOLIO 1) Si la curva de demanda que enfrenta el
Anuncio
MONOPOLIO
1) Si la curva de demanda que enfrenta el monopolista es P=200-10Q y su curva de costo marginal
Cmg=100+5Q. ¿Cuál es el precio y la producción que maximizan la ganancia del monopolio? Haga
los gráficos correspondientes.
Sabemos que la condición de maximización es IMa= CMa. Con esta condición encontramos la cantidad
que producirá el monopolista. Esta cantidad en conjunto con la demanda me permite encontrar el precio al
cual el monopolista venderá su producción.
IT=PQ es el ingreso total o ingreso por ventas del monopolio
Pero sabemos que el precio debe ser igual a P=200-10Q por la demanda. Podemos usar este precio que
nos da la demanda para reemplazarlo en los ingresos del monopolista.
Reemplazando el precio de la demanda en los ingresos:
IT=PQ=(200-10Q)Q=200Q-10Q2
Para encontrar el ingreso marginal, debemos encontrar la derivada del ingreso total.
IT (200Q 10Q 2 ) 200Q 10Q 2
Q
Q
Q
Q
IMa 200 20Q
IMa
Según los datos entregados el costo marginal es
CMa 100 5Q
La empresa monopólica maximiza su utilidad donde Img=Cmg.
IMa CMa
200 20Q 100 5Q
Q
100
4
25
Para encontrar el precio, usamos la cantidad encontrada Q=4 en la demanda de mercado:
P 200 10Q
Q4
P 200 10 * 4 200 40 160
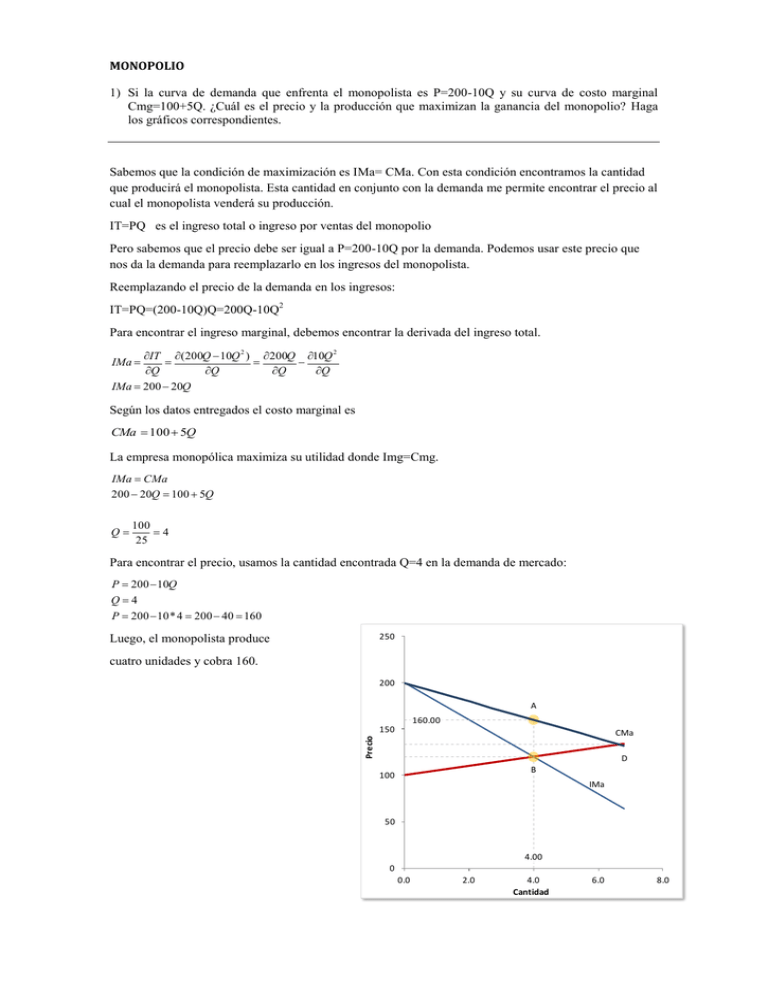
250
Luego, el monopolista produce
cuatro unidades y cobra 160.
200
A
160.00
150
Precio
CMa
D
B
100
IMa
50
4.00
0
0.0
2.0
4.0
Cantidad
6.0
8.0
1
2) Si la curva de demanda que enfrenta el monopolista es 𝑋 = 60 − 𝑃 y su curva de costo total
9
𝐶 = 300 + 95𝑋 + 16,75𝑋 2 + 0,25𝑋 3 ¿Cuál es el precio y la producción que maximizan la ganancia
del monopolio? Haga los gráficos correspondientes.
Sabemos que la condición de maximización es Img= Cmg. Con esta condición encontramos la cantidad
que producirá el monopolista. Esta cantidad en conjunto con la demanda me permite encontrar el precio al
cual el monopolista venderá su producción.
IT=PQ es el ingreso total o ingreso por ventas del monopolio
Pero sabemos que el precio debe ser igual a P=200-10Q por la demanda. Podemos usar este precio que
nos da la demanda para reemplazarlo en los ingresos del monopolista.
Reemplazando el precio de la demanda en los ingresos:
IT=PQ=
1
540
X
2
- 9,00
X
3
+ 0,00
X
Para encontrar el ingreso marginal, debemos encontrar la derivada del ingreso total.
1
IMa=
2
540 - 18,00 X
+ 0,00 X
Según los datos entregados el costo marginal es
1
CMa= 95,0 + 33,50
X
2
+ 0,75
X
La empresa monopólica maximiza su utilidad donde IMa=CMa.
X= 7,76
Para encontrar el precio, usamos la cantidad
encontrada en la demanda de mercado:
800
P =470,13
CMa
700
600
A
Precio
500
470,13
400
IMa
B
D
300
200
100
7,76
0
0,0
5,0
10,0
Cantidad
15,0
3) La curva de demanda de mercado para ciertos artefactos es P=100-5Q. La industria de estos artefactos
en la actualidad es un monopolio y la función de costo total del monopolista es CT=300+20Q.
Encuentre el equilibrio de mercado.
Sea P=100-5Q la demanda,
Sabemos que el ingreso total está dado por
IT=PQ
Reemplazamos el precio de la demanda en el ingreso total.
IT=[100-5Q]Q=100Q-5Q2
Calculemos el ingreso marginal derivando respecto a Q:
Im g
IT 100Q 5Q2
100Q 5Q2
100 10Q
Q
Q
Q
Q
El costo total según el enunciado es:
CT=300+20Q
Para encontrar el costo marginal, hay que derivar la función de costo total respecto a Q.
Cmg
CT 300 20Q 300 20Q
0 20
Q
Q
Q
Q
El punto en que el monopolista maximiza su beneficio económico donde Img=Cmg:
Im g 100 10Q Cmg 20
100 10Q 20
80 10Q
80
Q
10
Q8
Usando la cantidad para
120
calcular el precio de acuerdo a la demanda
100
P=100-5*8=100-40=60
Precio
80
A
60
60.00
40
D
20
CMa
B
8.00
Ima
0
0.0
5.0
10.0
Cantidad
15.0
20.0
1
4) La curva de demanda de mercado para ciertos artefactos es 𝑄 = 36 − 𝑃. La industria de estos
15
artefactos en la actualidad es un monopolio y la función de costo variable medio del monopolista es
𝐶𝑉𝑀𝑒 = 95 + 15,5 𝑄. Encuentre el equilibrio de mercado.
Sea P=540-15Q la demanda,
Sabemos que el ingreso total está dado por
IT=PQ
Reemplazamos el precio de la demanda en el ingreso total.
IT=[540-15Q]Q=540Q-15Q2
Calculemos el ingreso marginal derivando respecto a Q:
IMa= 540-30Q
El costo total según el enunciado es:
𝐶𝑇 = 𝐶𝐹 + 𝐶𝑉 = 𝐶𝐹 + 95𝑄 + 15,5𝑄2
Para encontrar el costo marginal, hay que derivar la función de costo total respecto a Q.
CMa= 95+31Q
El punto en que el monopolista maximiza su beneficio económico donde Img=Cmg:
540-30Q = 95+31Q
Q=7,30
Usando la cantidad para
calcular el precio de acuerdo a la demanda
P=540-15*7,30=430,57
600
CMa
500
A
430,57
Precio
400
D
300
B
IMa
200
100
7,30
0
0,0
5,0
10,0
Cantidad
15,0
5) Un monopolista con una función de costes totales iguales a 𝐶 𝑋 = 40𝑋 abastece a un mercado con
𝑝
una función de demanda igual a 𝑋 𝐷 = 100 – .
2
Obtenga:
a) El equilibrio del monopolista
b) Exprese el ingreso marginal en función del precio y la elasticidad precio de la demanda.
La C.P.O de maximización ed Beneficio requiere.
2 B( x) 2 I ( x) 2C ( x)
IMg CMg
IMg CMg
0
0
2
2
2
x
x
x
x
x
x
x
Para Max el beneficio del monopolista:
p( x) 200 2 x I ( x) p( x) x (200 x) x 200 x 2 x 2
I ( x)
IMg
200 4 x
x
Maxx B( x) 200 x 2 x2 40 x CMg C ( x) (40 x) 40
x
x
M
IMg CMg 200 4 x 40 x 40
Sustituyendo en la función inversa de demanda:
p M 200 2 x M 200 2 40 120
B M 120 40 40 40 3.200
La producción de equilibrio se corresponde al punto de corte de
las curvas de ingreso marginal y coste marginal. El precio de equilibrio
viene determinado por la curva de demanda para ese nivel de producción
250
200
Precio
150
A
120,00
100
CMa
D
50
B
40,00
0
0,0
20,0
40,0
60,0
Cantidad
80,0
100,0
2. El ingreso marginal puede expresarse en función del
precio y la elasticidad precio de la demanda:
IMg
I ( x)
p( x)
x p( x)
p ( x) x
p( x)(1
)
x
x
p( x) x
IMg
I ( x)
1
1
p( x)(1
) IMg p( x)(1
)
x
x, p
x, p
0 si x, p >1 (el equilibrio se produce en este tramo elástico)
IMg
0 si x, p =1
0 si x, p <1
En términos de los datos del problema:
x, p x p 1 120 1,5 x, p 1,5 1
p x
2 40
El IMg en equlibrio es igual a 40.
IMg p( x)(1
1
) 120(1
1
) p( x)(1
x, p
1
) 40
1,5
NOTA :
IMg p( x)(1
L
x, p
1
x, p
) CMg p( x) (
p( x) CMg
1
1
120 40
0, 6
p ( x)
x, p x, p
120
x, p
)CMg
x, p 1
DISCRIMINACION DE PRECIOS:
La única cooperativa agrícola dedicada a la producción y comercialización de la variedad de uva D.O.
tiene dos grupos de consumidores potenciales. El primer grupo engloba a las bodegas de la zona, con una
función de demanda 𝑥1𝐷 = 100 − 2𝑃1 . El segundo grupo está formado por los comerciantes de
la zona, con una función de demanda 𝑥2𝐷 = 100 − 𝑃2 . La función de coste del monopolista es
𝐶 𝑋 = 5𝑋 + 1500. Entre ambos grupos no hay posibilidad de reventa. La cooperativa vende la caja de
uvas (𝑋) a 30 € a la bodega y a 50€ a los comerciantes siendo 𝑋 = 𝑥1 + 𝑥2 .
a) Tiene la cooperativa un comportamiento maximizador de beneficios?. Si no es así, ¿cuáles serían los
precios a los que debería vender a cada grupo para maximizar beneficios?.
b) El director de la cooperativa quiere aumentar la cifra de beneficios. Analice si realizar una subasta en
la que cada consumidor paga un precio distinto por la caja de uvas consigue dicho objetivo.
1. En este problema, el monopolista -la cooperativa- puede
realizar discriminación de tercer grado -mercados separados y
no hay posibilidad de reventa -.
Maxx1 , x2 B( x) I ( x1 ) I ( x2 ) C ( x) p( x1) x1 p( x2 ) x2 C ( x)
C.P.O
IMg1 CMg 0
IMg1 IMg 2 CMg
IMg 2 CMg 0
100 x1
Maxx1 , x2 B( x) (
) x1 (100 x2 ) x2 (5 x 1.500)
2
Si el monopolista vende a los precios de 30 y 50, no
Max. el Beneficio
Por las C.P.O tenemos:
IMg1 CMg 50 x1 5
x1* 45
*
x2 47,5
IMg2 CMg 100 2 x2 5
* 100 x1*
27,5
p1
2
p* 100 x* 52,5
2
2
x1 ( p1 30) 100 2 p1 40
x2 ( p2 50) 100 p2 50
B 30 40 50 50 5 90 1.500 1.750
La producción de equilibrio y los precios de equilibrio son:
Si el monopolista realiza discriminación de tercer grado el
beneficio de equilibrio sería:
x* x1* x2* 45 47,5 92,5
B* 27,5(45) 52,5(47,5) 5(92,5) 1.500 1.768, 75
B* B
Nótese que para p1 =30 y p2 =50 las cantidades ofertadas son
40 y 50 unidades respectivamente. En este caso los IMg en
los mercados serían:
IMg1 ( x1 40) 50 40 10
IMg1 IMg 2
IMg2 ( x2 50) 100 2 50 0
La empresa puede incrementar sus beneficios aumentando
la producción en el mercado 1 y reduciendo la del mercado 2.
El equilibrio se encuentra en el punto E*
Si el monopolista vende a los precios de 30 y 50, no
Max. el Beneficio
* 100 x1*
27,5
p1
2
*
*
p 100 x 52,5
2
2
x1 ( p1 30) 100 2 p1 40
x2 ( p2 50) 100 p2 50
B 30 40 50 50 5 90 1.500 1.750
Si el monopolista realiza discriminación de tercer grado el
beneficio de equilibrio sería:
B* 27,5(45) 52,5(47,5) 5(92,5) 1.500 1.768, 75
B* B
2. El monopolista puede realizar discriminación de tercer grado. Es decir, el
monopolista se apropia del excedente de los consumidores.
El ingreso del monopolista coincide con el área por debajo de la curva de
demanda para la cantidad vendida (área sombreada).
Con los datos del ejercicio:
1
2
100 x1
Maxx1, x2 B( x) (
)dx1 (100 x2 )dx2 (5x 1.500)
2
0
0
x
x
C.P.O
B( x) 100 x1
5 0
x1
2
xˆ1 90
xˆ 185
xˆ2 95
B( x)
100 x2 5 0
x2
La cantidad total vendida coincide con la de Comp. perfecta, ya que
el precio al que el monopolista vende la última unidad en ambos
mercados es p=CMg=5.
El beneficio de la cooperativa es:
90
95
100 x1
Bˆ (
)dx1 (100 x2 )dx2 (5 185 1.500)
2
0
0
50 x1
90
95
x12
x22
100 x2 2.425 5.037,5
4 0
2 0
Los beneficios de realizar discriminación perfecta son
superiores a los que se obtendrían al realizar discriminación
de tercer grado.
Bˆ B *
DISCRIMINACION DE PRECIOS Y MULTIPLES PLANTAS:
Una empresa monopolista exporta toda su producción a Francia y a Italia. El precio de la demanda de
𝑞
Francia es 𝑃𝐹 = 50 − 𝐹 , mientras que la cantidad demandada en Italia es igual a 𝑞𝐼 = 200 − 2𝑝𝐼 . Para
2
poder satisfacer a la demanda, esta empresa posee dos plantas de producción, cuyos costos vienen dados
𝑞2
por: 𝐶1 = 100 + 1 y 𝐶1 = 50 +
8
beneficios de este productor.
𝑞 22
4
. Halle los precios y las cantidades de equilibrio que maximizan los
Datos:
𝑞
𝑃𝐹 = 50 − 𝐹
2
𝑞𝐼 = 200 − 2𝑝𝐼
eq. (1)
eq. (2)
𝐶1 = 100 +
eq. (3)
𝐶2 = 50 +
𝑞 22
𝑞 12
8
4
eq. (4)
¿Qué sabemos?
La demanda indirecta de Italia es:
1
𝑝𝐼 = 100 − 𝑞𝐼
2
eq. (5)
Por lo tanto las funciones de Ingresos y de Costos son:
𝑞
𝐼𝐹 = 𝑃𝐹 𝑞𝐹 = (50 − 𝐹 )𝑞𝐹
eq.(6)
𝐼𝐼 = 𝑃𝐼𝑞 𝐼 = 100 − 𝑞𝐼 𝑞𝐼
eq. (7)
2
1
2
𝐶𝑇 = 𝐶1 + 𝐶2 = 100 +
𝑞 12
8
+ 50 +
𝑞 22
4
= 150 +
𝑞 12
8
+
𝑞 22
eq. (8)
4
También debemos entender que la cantidad total producida (𝑄𝑃 ) ha de ser igual a la cantidad total
vendida (𝑄𝑉 ). Es decir, 𝑄𝑃 = 𝑄𝑉 :
𝑄𝑉 = 𝑞1 + 𝑞2
𝑄𝑃 = 𝑞𝐹 + 𝑞𝐼
Es decir: 𝑞1 + 𝑞2 = 𝑞𝐹 + 𝑞𝐼
⟹
𝑞𝐹 = 𝑞1 + 𝑞2 − 𝑞𝐼
eq. (9)
La importancia de este supuesto, es que nos permite relacionar la discriminación de precios hacia los
mercados de Francia e Italia, con la producción atendida en múltiples plantas. Esto se logra combinando
la eq. (9) en la eq. (6) de la siguiente manera:
𝐼𝐹 = 𝑃𝐹 𝑞𝐹 = 50 −
𝑞 1 +𝑞 2 −𝑞 𝐼
2
(𝑞1 + 𝑞2 − 𝑞𝐼 )
eq. (10)
Por lo tanto, para construir la función de beneficios (π) usaremos las ecuaciones 7, 8 y 10:
𝜋 = 50 −
𝑞 1 +𝑞 2 −𝑞 𝐼
𝑞1 + 𝑞2 − 𝑞𝐼 + 200 − 2𝑞𝐼 𝑞𝐼 − 150 +
2
𝐼𝐹
𝐼𝐼
𝑞 12
8
+
𝑞 22
4
𝐶𝑇
Simplificando podremos decir que para maximizar los beneficios debemos establecer que:
𝑀𝑎𝑥.
𝑞𝐹 , 𝑞1 , 𝑞2
5
3
8
4
𝜋 𝑞𝐹 , 𝑞1 , 𝑞2 = 50𝑞1 − 𝑞12 − 𝑞1 𝑞2 + 𝑞1 𝑞𝐼 + 50𝑞2 − 𝑞22 + 𝑞2 𝑞𝐼 + 50𝑞𝐼 − 𝑞𝐼2 − 150
C.P.O.
𝛿𝜋
𝛿 𝑞𝐼
𝛿𝜋
𝛿 𝑞1
𝛿𝜋
𝛿 𝑞2
= 𝑞1 + 𝑞2 + 50 − 𝑞𝐼
= 50 −
10
8
𝑞1 − 𝑞2 + 𝑞𝐼
𝒒∗𝑰 = 𝟑𝟏, 𝟐𝟓
=0
=0
6
= −𝑞1 + 50 − 𝑞2 + 𝑞𝐼 = 0
4
⟹
𝒒∗𝟏 = 𝟕𝟓
𝒒∗𝟐 = 𝟑𝟕, 𝟓
Utilizando la eq. (9) sabemos que:
𝒒∗𝑭 = 𝟖𝟏, 𝟐𝟓
Donde los precios de equilibrio serán:
𝑷∗𝑭 = 𝟑𝟒, 𝟑𝟕𝟓
Y donde los beneficios serán iguales a:
𝝅 = 𝟒𝟔𝟗𝟑, 𝟕𝟓
y
𝑷∗𝑰 = 𝟓𝟗, 𝟑𝟕𝟓
eq. (11)
COMPENTENCIA MONOPOLÍSTICA:
El mercado de detergente (𝑥) formado por cinco empresas, está caracterizado por una situación de
competencia monopolística. Las funciones de demanda y costes son iguales para todas las empresas,
siendo. Demanda: 𝑝𝑖 = 8,25 − 𝑥𝑖 − 0,2 𝛴𝑗𝑛≠ 𝑖 𝑥𝑗
Costes: 𝐶𝑖 = 𝑥𝑖3 − 2𝑥𝑖2 + 3𝑥𝑖 .
Determine el equilibrio de una empresa representativa y del mercado y represéntelo gráficamente en los
siguientes casos:
a) Si existen barreras a la entrada y el número de empresas está dado.
b) Si “No” existe libertad de entrada al mercado.
Datos si existen barreras a la entrada n=5:
Demanda:
{ 𝑥1𝐷 , 𝑥2𝐷 , 𝑥3𝐷 , 𝑥4𝐷 , 𝑥5𝐷 } = { 𝑥1𝐷 ,…, 𝑥𝑖𝐷 , …, 𝑥5𝐷 } = 𝑝𝑖 = 8,25 − 𝑥𝑖 − 0,2 𝛴𝑗𝑛≠ 1 𝑥𝑗
Costos:
𝐶𝑖 = 𝑥𝑖3 − 2𝑥𝑖2 + 3𝑥𝑖
Problema de la empresa representativa:
𝑀𝑎𝑥.
𝑋𝑖
𝜋 𝑋𝑖 = 𝐼𝑖 − 𝐶𝑖 = 𝑝𝑖 𝑥𝑖 − 𝐶𝑖 =
𝜋 𝑋𝑖 = 8,25 − 𝑥𝑖 − 0,2 𝛴𝑗𝑛≠ 1 𝑥𝑗 𝑥𝑖 − 𝑥𝑖3 − 2𝑥𝑖2 + 3𝑥𝑖
C.P.O.
𝛿𝜋
𝛿 𝑥𝑖
=0
Dado que n=5
8,25 − 2𝑥1 − 0,2 𝑥2 + 𝑥3 + 𝑥4 + 𝑥5 − 3𝑥12 − 4𝑥1 + 3=0
8,25 − 2𝑥2 − 0,2 𝑥1 + 𝑥3 + 𝑥4 + 𝑥5 − 3𝑥22 − 4𝑥2 + 3=0
8,25 − 2𝑥3 − 0,2 (𝑥1 + 𝑥2 + 𝑥4 + 𝑥5 ) − 3𝑥32 − 4𝑥3 + 3=0
𝑥 ∗1 = 𝑥 ∗ 2 = 𝑥 ∗ 3 = 𝑥 ∗ 4 = 𝑥 ∗ 5
8,25 − 2𝑥4 − 0,2 (𝑥1 + 𝑥2 + 𝑥3 + 𝑥5 ) − 3𝑥42 − 4𝑥4 + 3=0
8,25 − 2𝑥5 − 0,2 (𝑥1 + 𝑥2 + 𝑥3 + 𝑥4 ) − 3𝑥52 − 4𝑥5 + 3=0
Entonces podemos simplificar el problema a tan solo decir que:
8,25 − 2𝑥𝑖 − 0,2 4 𝑥𝑖 − 3𝑥𝑖2 − 2𝑥𝑖 + 3 = 0
3𝑥𝑖2 − 1,2𝑥𝑖 − 5,25 = 0
⟹
𝑥𝑖 =
1,2 (+/−) 1,2 2 −4∗3∗ −5,25
2∗3
⟹
Precio:
𝑝𝑖 = 8,25 − 1,538 − 0,2 ∗ 4 ∗ (1,538) = 5,481
Note que con barreras de entradas sucede que:
𝐶𝑀𝑒𝑖 =
𝐶𝑖 𝑥𝑖3 − 2𝑥𝑖2 + 3𝑥𝑖
=
= 𝑥𝑖2 − 2𝑥𝑖 − 3 = 1,538
𝑥𝑖
𝑥𝑖
Y donde los beneficios serán iguales a:
2
− 2 ∗ 1,538 − 3 = 2,289
𝝅 = 𝟒, 𝟗𝟏 > 0
𝒙∗𝒊 = 𝟏, 𝟓𝟑𝟖
Datos si no existen barreras a la entrada:
Demanda:
{ 𝑥1𝐷 ,…, 𝑥𝑖𝐷 , …, 𝑥𝑛𝐷 } = 𝑝𝑖 = 8,25 − 𝑥𝑖 − 0,2 𝛴𝑗𝑛≠ 1 𝑥𝑗 hasta que el 𝑃𝑖 = 𝐶𝑀𝑒𝑖
Costos:
𝐶𝑖 = 𝑥𝑖3 − 2𝑥𝑖2 + 3𝑥𝑖
Problema de la empresa representativa:
𝑀𝑎𝑥.
𝑋𝑖
𝜋 𝑋𝑖 = 8,25 − 𝑥𝑖 − 0,2 𝛴𝑗𝑛≠ 1 𝑥𝑗 𝑥𝑖 − 𝑥𝑖3 − 2𝑥𝑖2 + 3𝑥𝑖
Sujeto a que:
𝑃𝑖 = 𝐶𝑀𝑒𝑖
C.P.O.
𝛿𝜋
𝛿 𝑥𝑖
8,25 − 2𝑥𝑖 − 0,2 𝛴𝑗𝑛≠ 1 𝑥𝑗 − 3𝑥12 − 4𝑥1 + 3 = 0
=0
8,25 − 𝑥𝑖 − 0,2 𝛴𝑗𝑛≠ 1 𝑥𝑗 = 𝑥𝑖2 − 2𝑥𝑖 + 3
𝑃𝑖 = 𝐶𝑀𝑒𝑖
Como 𝑥1 = 𝑥2 = … = 𝑥𝑖 = … = 𝑥𝑛 = 𝑥𝑖∗ entonces podemos decir que
𝛴𝑗𝑛≠ 1 𝑥𝑗 = 𝑛 − 1 𝑥𝑖
𝛿𝜋
𝛿 𝑥𝑖
=0
𝑃𝑖 = 𝐶𝑀𝑒𝑖
8,25 − 2𝑥𝑖 − 0,2 𝑛 − 1 𝑥𝑖 − 3𝑥12 − 4𝑥1 + 3 = 0
𝒙∗𝒊 = 𝟎, 𝟓
8,25 − 𝑥𝑖 − 0,2 𝑛 − 1 𝑥𝑖 = 𝑥𝑖2 − 2𝑥𝑖 + 3
𝒏∗ = 𝟓𝟔
𝑷𝒊 = 𝑪𝑴𝒆𝒊 = 𝟐, 𝟐𝟓
Gráficas Competencia Monopolística
Corto plazo
Largo Plazo
CM
CM
CMe
P*i=5,481
CMe
P*i=CMe*i=2,25
CMe*i=2,289
P(xi)
IM(xi)
X*i=1,538
IM(xi)
X*i=0,5
X*i=1,538
P(xi)
MERCADOS IMPERFECTOS (OLIGOPOLIO):
1) Un mercado con una curva inversa de demanda 𝑃 𝑋 = 100 − 𝑋 es abastecido por dos empresas
cuyas funciones de costes son: 𝐶 𝑥1 = 4𝑥1 y 𝐶 𝑥2 = 2𝑥22 . Determine el equilibrio de cada
empresa en los siguientes casos:
i) Obtenga el equilibrio si las dos empresas consideran al mismo tiempo la reacción de su rival ante
cambios en las cantidades (Modelo de Cournot)
ii) Analice si estas empresas tienen incentivos a formar un cártel si el beneficio conjunto se
distribuye según la cuota de mercado de cada empresa.
iii) Analice si una vez formado el cártel, la empresa 2 tiene incentivos a romper el acuerdo.
iv) Calcule el equilibrio si la empresa 1 actúa como líder en cantidades
(Modelo de Stackelberg)
Respuesta:
a) Modelo de Cournot: “Las empresas compiten entre sí pero toman sus decisiones de manera
simultánea”
Problemas de la empresa 1
𝑀𝑎𝑥.
𝑥1
Problemas de la empresa 2
𝑀𝑎𝑥.
𝑥2
𝜋 𝑥1 = 100 − 𝑥1 − 𝑥2 𝑥1 − 4𝑥1
C.P.O.
𝛿𝜋
𝛿 𝑥𝑖
=0
𝜋 𝑥2 = 100 − 𝑥1 − 𝑥2 𝑥2 − 2𝑥22
C.P.O.
𝛿𝜋
100 − 𝑥1 − 𝑥2 − 4 = 0
𝑥1 =
96−𝑥 2
2
𝛿 𝑥𝑖
=0
100 − 𝑥1 − 2𝑥2 − 4𝑥2 = 0
𝑥2 =
“Curva reacción 1”
100 −𝑥 1
6
“Curva reacción 2”
Igualando las curvas de reacción:
𝐶𝑅 𝑥1 = 𝐶𝑅 𝑥2
𝑥1 =
=>
100 −𝑥 1
)
6
96−(
=>
2
𝑥1𝐶𝑂 = 43,27 , 𝑥2𝐶𝑂 = 9,5
Donde el precio es igual:
𝑃𝐶𝑂 = 100 − 𝑋 𝐶𝑂 = 100 − 52,72 = 47,28
Y el beneficio de cada empresa es:
𝛱1𝐶𝑂 = 1872,53
𝛱2𝐶𝑂 = 268,16
𝛱𝐶𝑂 = 2140,69
Empresa 2
Fig. Curvas de Reacción en cantidades
Empresa 1 Vs. Empresa 2
100
90
80
70
60
50
40
30
20
10
9.45
43.27
0
0
10
20
30
40
50
60
70
80
90 100
Cantidad Empresa 1
y 𝑋 𝐶𝑂 = 52,72
b) Situación del Cartel o Colusión: “En el cartel las empresas no compiten entre si, sino que cooperan o
coluden para maximizar sus beneficios conjunto. Para esto actuan como fuesen una empresa con
múltiples plantas”
Por lo tanto el problema en colusión plantea que:
𝑀𝑎𝑥.
𝑋
𝜋 𝑋 = 100 − 𝑋 𝑋 − 4𝑥1 − 2𝑥22
Ingreso del
Coste
Coste
Cartel
Empresa 1 Empresa 2
C.P.O.
𝛿𝐼
𝐼𝑀 = 𝐶𝑀1
𝛿𝑋
𝐼𝑀 = 𝐶𝑀2
𝛿𝑋
𝛿𝐼
=
=
𝛿𝐶1
𝛿𝑥 1
𝛿𝐶2
𝛿𝑥 2
100 − 𝑋 = 4
𝑋 𝐶𝐴 = 48
100 − 2𝑥 = 4𝑥2
𝑥2𝐶𝐴 = 1
Donde: 𝑥1𝐶𝐴 = 48 − 1 = 47
Donde el precio es igual:
𝑃𝐶𝐴 = 100 − 𝑋 𝐶𝐴 = 100 − 48 = 52
Y el beneficio de cada empresa es:
𝛱1𝐶𝐴 = 2256
𝛱2𝐶𝐴 = 50
𝛱𝐶𝐴 = 2306
c) ¿La empresa 2 tiene incentivos para formar un cartel?
En en el equilibrio de Cournot:
El beneficio de cada empresa es:
𝛱1𝐶𝑂 = 1872,53
𝛱2𝐶𝑂 = 268,16
𝛱𝐶𝑂 = 2140,69
𝛱1𝐶𝐴 = 2256
𝛱2𝐶𝐴 = 50
𝛱𝐶𝐴 = 2306
En en el equilibrio del Cartel:
Y el beneficio de cada empresa es:
Obviamente los beneficios conjuntos del cartel son mayores que los beneficios individuales:
𝛱𝐶𝑂 = 2140,69 < 𝛱𝐶𝐴 = 2306
¿Qué hacer?
Si comparamos los beneficios tenemos que: 𝛱𝐶𝐴 − 𝛱𝐶𝑂 = 2306 − 2140,69 = 165,31
Alternativa A: (distribuir los beneficios extraordinarios por partes iguales)
𝛱1𝐴 = 𝛱1𝐶𝑂 +
𝛱2𝐴 = 𝛱2𝐶𝑂
165 ,31
= 1872,53 + 82,65 = 1955,18
165,31
+
= 268,16 + 82,65 = 350,81
2
2
Alternativa B: (proporcional a nivel de producción)
𝑥1𝐶𝑂 % =
𝑥2𝐶𝑂 % =
43,2
52,72
= 82%
9,5
= 18%
52,72
𝛱1𝐴 = 𝛱1𝐶𝑂 + 165,31 ⋅ 82% = 1872,53 + 135,55 = 2008,08
𝛱2𝐴 = 𝛱2𝐶𝑂 + 165,31 ⋅ 18% = 268,16 + 29,76 = 297,92
¿Otra alternativa?
Que tal si las empresas firman el acuerdo de la alternativa A. Es decir, pactamos a partes iguales
las ganancias extraordinarias. En esta situación, deben acordar que la empresa “1” produzca
𝒙𝟏 = 𝟒𝟕 y la empresa “2” 𝒙𝟐 = 𝟏
¿Qué sucede si la empresa “1” rompe el acuerdo? ¿Esto puede tener algún sentido?
Analizando esta situación de la empresa individual sabemos que si la otra empresa cumple el acuerdo…
…. la reacción óptima para maximizar beneficios debe ser:
𝑥1 =
96−𝑥 2
2
=
96−1
2
95
=
2
= 47,5
Por lo tanto:
Dado que la Empresa “2” produce 𝑥2 = 1 implicaría que la oferta total es: 𝑋 = 48,5
Es decir, el precio es igual a P=100-48,5=51,5
𝛱1∗ = 2256,25
𝛱2∗ = 49,5
Y el beneficio de cada empresa es:
𝛱 ∗ = 2305,75
¿Qué sucede si la empresa “2” rompe el acuerdo? ¿Esto puede tener algún sentido?
Analizando esta situación de la empresa individual sabemos que si la otra empresa cumple el acuerdo…
…. la reacción óptima para maximizar beneficios debe ser:
𝑥2 =
100 −𝑥 1
6
=
96−47
6
=
49
6
= 8,16
Por lo tanto:
Dado que la Empresa “1” produce 𝑥1 = 47 implicaría que la oferta total es: 𝑋 = 55,166
Es decir, el precio es igual a P=100-55,16=44,833
Y el beneficio de cada empresa es:
𝛱1∗∗ = 1919,15
𝛱 ∗∗ = 2151,92
∗∗
𝛱2 = 232,77
En resumen:
Resumen de los beneficios
bajo distintos escenarios
Empresa 2
Cournot
Cartel
Cournot
𝛱1𝐶𝑂 = 1872,53
𝛱2𝐶𝑂 = 268,16
𝛱1∗ = 2256,25
𝛱2∗ = 49,5
Cartel
𝛱1∗∗ = 1919,15
𝛱2∗∗ = 232,77
𝛱1𝐶𝐴 = 1955,18
𝛱2𝐶𝐴 = 350,81
Empresa 1
Dados estos resultados ¿Cuál de todas esta situaciones sería la que ocurriría?
Resumen de los beneficios
bajo distintos escenarios
Empresa 2
Cournot
Cartel
Cournot
𝛱1𝐶𝑂 = 1872,53
𝛱2𝐶𝑂 = 268,16
𝛱1∗ = 2256,25
𝛱2∗ = 49,5
Cartel
𝛱1∗∗ = 1919,15
𝛱2∗∗ = 232,77
𝛱1𝐶𝐴 = 1153
𝛱2𝐶𝐴 = 1153
Empresa 1
d) Equilibrio si la empresa 1 actúa como líder en cantidades (Modelo de Stackelberg)
Problema de la empresa “1” como “líder”
𝑀𝑎𝑥.
𝑥1
𝜋 𝑥1 = 100 − 𝑥1 − 𝑥2 𝑥1 − 4𝑥1
…pero sabemos que: 𝑥2 =
𝑀𝑎𝑥.
𝑥1
𝜋 𝑥1 = 100 − 𝑥1 −
𝑀𝑎𝑥.
𝑥1
𝜋 𝑥1 =
500 𝑥 1 −5𝑥 12
6
100 −𝑥 1
100 −𝑥 1
6
6
𝑥1 − 4𝑥1 =
600 −6𝑥 1 −100 +𝑥 1
6
𝑥1 − 4𝑥1 =
500 −5𝑥 1
6
𝑥1 − 4𝑥1
− 4𝑥1
C.P.O.
𝛿𝜋
𝛿 𝑥𝑖
500 −10𝑥 1
=0
6
−4=0
=>
500 − 10𝑥1 = 24
𝑥1 = 47,6
=>
𝑥2 =
100 −47,6
6
= 8,733
Por lo tanto:
Acutando la empresa “1” como líder, y la empresa “2” como seguidora tenemos que la oferta total es:
𝑋 = 56,33
Es decir, el precio es igual a P=100-56,33=43,66
Y el beneficio de cada empresa es:
𝛱1∗ = 1887,82
𝛱2∗ = 228,23
𝛱 ∗ = 2116,05
2) Dos empresas 1 y 2, están eligiendo simultáneamente las cantidades 𝑞1 y 𝑞2 , que van a producir de
un producto homogéneo. El costo total de producir 𝑞𝑖 por la empresa 𝑖 es 𝐶𝑇𝑖 = 7 𝑞𝑖 para todo
𝑖 = 1,2; donde la cantidad agregada en el mercado es 𝑄 = 𝑞1 + 𝑞2 . De igual manera, se sabe que la
demanda es tal que 𝑄𝐷 (𝑃) = 70 − 𝑃. Determine los equilibrios (precios y cantidades), así como los
beneficios en cada situación:
i) Las dos empresas consideran al mismo tiempo la reacción de su rival ante cambios en las
cantidades.
ii) Las dos empresas acuerdan cooperar coludiendo en cantidades para maximizar el beneficio
conjunto.
iii) Si una de las empresas incumple el acuerdo anterior: ¿qué sucedería con los beneficios?
iv) Desde el punto de vista de la teoría de juegos ¿Qué tipo de juego representan los resultados
obtenidos? ¿Tienen las empresas una estrategia dominante? ¿Existe un equilibrio de Nash?
i)
Las dos empresas consideran al mismo tiempo la reacción de su rival ante cambios en las
cantidades
Datos:
𝐶𝑇1 = 7𝑞1
𝐶𝑇2 = 7𝑞2
𝑄 = 𝑞1 +𝑞2
𝑃 = 70 − 𝑄
ó 𝑃 = 70 − 𝑞1 − 𝑞2 .
Corresponde a un planteamiento de Cournot. Problema de maximización de la empresa
representativa 𝑖 (hacer esto es lo mismo que hacerlo para la empresa 1 ó la empresa 2 de manera
simultánea)
Max 𝐵𝑖 = 𝑃𝑞𝑖 – 𝐶𝑇𝑖 = 70 − 𝑞𝑖 − 𝑞𝑗 𝑞𝑖 – 7𝑞𝑖 = 70𝑞𝑖 − 𝑞𝑖2 − 𝑞𝑖 𝑞𝑗 – 7𝑞𝑖 = 63𝑞𝑖 − 𝑞𝑖2 − 𝑞𝑖 𝑞𝑗
CPO:
𝑑𝐵
𝑑𝑞 𝑖
=0
𝑑𝐵
𝑑𝑞 𝑖
= 63 − 2𝑞𝑖 − 𝑞𝑗 = 0 𝑞𝑖 =
63−𝑞 ∗
∗
𝑞 =
2
63−𝑞 𝑗
2
𝑞1 =
𝑞2 =
63−𝑞 2
2
63−𝑞 1
simetría 𝑞1∗ = 𝑞2∗ = 𝑞 ∗
2
∗
𝑞 = 21
Respuesta: Q=21+21=42
P=70-42=28
𝐵1 = 28 ⋅ 21 − 7 ⋅ 21 = 441
𝐵2 = 28 ⋅ 21 − 7 ⋅ 21 = 441
Empresa 2
𝑞1∗ = 𝑞2∗ = 21
70
60
50
40
30
21.00
20
10
21.00
0
0
10
20
30
40
50
60
70
Cantidad Empresa 1
ii)
Las dos empresas acuerdan cooperar como un cartel para maximizar el beneficio conjunto.
¿Qué sucedería con los beneficios si alguna no cumple con los acuerdos?
Corresponde a un planteamiento de Cartel:
Max
𝐵𝑐𝑎𝑟𝑡𝑒𝑙 = 𝑃𝑄– 𝐶𝑇1 − 𝐶𝑇2 = 70 − 𝑞𝑖 − 𝑞𝑗
2
𝑞2 − 2𝑞1 𝑞2
𝑑𝐵 𝑐𝑎𝑟𝑡𝑒𝑙
CPO:
𝑑𝑞 1
𝑑𝐵 𝑐𝑎𝑟𝑡𝑒𝑙
𝑑𝑞 1
=0
y
𝑑𝐵 𝑐𝑎𝑟𝑡𝑒𝑙
𝑑𝑞 2
𝑞𝑖 + 𝑞𝑗 – 7𝑞𝑖 − 7𝑞𝑗 = 63𝑞1 + 63𝑞2 − 𝑞12 −
=0
= 63 − 2𝑞1 − 2 𝑞2 = 0
Simetría 𝑞1∗ = 𝑞2∗ = 𝑞 ∗ 𝑞 ∗ =
𝑑𝐵 𝑐𝑎𝑟𝑡𝑒𝑙
𝑑𝑞 2
63−2𝑞 ∗
2
𝑞 ∗ = 15,75
= 63 − 2𝑞2 − 2 𝑞1 = 0
Respuesta: Q=15,75+15,75=31,5
P=70-31,5=38
𝐵1 = 38 ⋅ 31,5 − 7 ⋅ 15,75 = 992,25
𝐵2 = 38 ⋅ 31,5 − 7 ⋅ 15,75 = 992,25
iii)
𝑞𝑖 =
Si rompe el acuerdo entonces una de ellas produce 𝑞𝑗 = 15,75 conociendo las funciones de
reacción, entonces:
63−15,75
2
= 23,625
Respuesta:
Q=23,625+15,75=39,375
P=70-39,375=30,625
𝐵1 = 30,625 ⋅ 23,625 − 7 ⋅ 23,625 = 558,145
𝐵2 = 30,625 ⋅ 15,750 − 7 ⋅ 15,750 = 372,094
iv)
Desde el punto de vista de la teoría de juegos ¿Qué tipo de juego representan los resultados
obtenidos? ¿Tienen las empresas una estrategia dominante? ¿Existe un equilibrio de Nash?
Empresa 2
Empresa
1
1)
Cournot
Cartel
Cournot
441 , 441
558 , 372
Cartel
373 , 558
992 , 992
Suponga un juego con dos empresas que deciden simultáneamente acerca de la estrategia de precios
a seguir. La empresa 1 se plantea elegir entre seguir manteniendo los precios, o bajarlos, mientras
que la empresa 2 se plantea entre subirlos o bajarlos. La matriz de pagos de este juego es el
siguiente:.
Empresa 2
Subirlos
Bajarlos
Empresa
1
i)
Mantenerlos
441 , 442
558 , 372
Bajarlos
373 , 558
497 , 498
¿Tiene alguna empresa una estrategia dominante?
No existe estrategia dominante!!!!!
Conjunto de la Emp. 1 si mantiene precio {441,558}
Conjunto de la Emp. 1 si baja precios
{373,497} no existe la posibilidad que un conjunto
domine a otro
Conjunto de la Emp. 2 si sube precio
Conjunto de la Emp. 2 si baja precios
domine a otro
ii)
{442,558}
{372,498} no existe la posibilidad que un conjunto
¿Existe un equilibrio de Nash?
El equilibrio de Nash es: Emp1 mantiene precios y Empresa 2 sube precios
iii) ¿Cuál situación es un resultado óptimo de Pareto?
La situación óptima de Pareto es donde en conjunto las empresas maximizan sus beneficios,
es decir, la situación bajar-bajar
MERCADOS IMPERFECTOS – OLIGOPOLIO PRECIOS (Modelo de Bertran):
Suponga que existen dos empresas, 1 y 2, que eligen simultáneamente los precios 𝑝1 y 𝑝2 a los que estarían
dispuestos a ofrecer un bien que producen (no diferenciado). Si es conocido por todos que la demanda de los
consumidores es tal que: 𝑞𝑖 𝑝𝑖 , 𝑝𝑗 = 𝑎 – 𝑝𝑖 + 𝑝𝑗 .
i)
Determine el equilibrio de Bertrand-Nash de esta situación.
ii)
¿Es este equilibrio eficiente en el sentido de Pareto?
El modelo de Bertrand es un modelo de competencia imperfecta nombrada en honor de Joseph Louis
François Bertrand (1822-1900). En este se supone que las interacciones entre vendedores (empresas) se
da por medio de la fijación de los precios, donde los compradores decidan cuanto comprar a ese precio.
En este caso se resuelve similar al modelo de Cournot, pero sustituyendo la cantidad por el “precio” como
variable estratégica. Por lo tanto el problema se plantea como:
𝑀𝑎𝑥.
𝑝𝑖
𝜋 𝑝𝑖 , 𝑝𝑗 = 𝑝𝑖 ∙ 𝑞 𝑝𝑖 , 𝑝𝑗 − 𝐶𝑀𝑖 ∙ 𝑞𝑖
Ingresos
Costos
C.P.O.
𝛿𝜋
𝛿 𝑝𝑖
𝛿𝜋
=0
𝛿 𝑝𝑖
𝛿𝜋
𝛿 𝑝𝑖
𝛿𝜋
𝛿 𝑝𝑖
=
=
𝛿[𝑝 𝑖∙ 𝑞 𝑖 −𝐶𝑀𝑖 ∙𝑞 𝑖 ]
𝛿𝑝 𝑖
=
𝛿[𝑝 𝑖∙ 𝑎−𝑝 𝑖 +𝑝 𝑗 −𝐶𝑀𝑖 ∙(𝑎−𝑝 𝑖 +𝑝 𝑗 )]
𝛿𝑝 𝑖
𝛿[𝑝 𝑖 ∙𝑎−𝑝 𝑖2 +𝑝 𝑖 ∙𝑝 𝑗 −𝑎∙𝐶𝑀𝑖 +𝐶𝑀𝑖 ∙𝑝 𝑖 −𝐶𝑀𝑖 ∙𝑝 𝑗 ]
𝛿𝑝 𝑖
= 𝑎 − 2𝑝𝑖 + 𝑝𝑗 + 𝐶𝑀𝑖 = 0
𝑝𝑖 =
𝑎+𝑝 𝑗 +𝐶𝑀𝑖
2
=0
=0
por lo tanto despenjando 𝑝𝑖
“Función de mejor respuesta de 𝑖 = 1,2
Por lo tanto en equilibrio se debe satisfacer que:
𝑝1 =
𝑝2 =
𝑎+𝑝 2 +𝐶𝑀1
2
𝑎+𝑝 1 +𝐶𝑀2
2
Suponiendo que son indénticas tenemos que 𝐶𝑀1 = 𝐶𝑀2 = 𝐶𝑀
𝑝1∗ = 𝑝2∗ = 𝑎 + 𝐶𝑀
Y la cantidad de equilibrio es por lo tanto:
𝑞𝑖∗ = 𝑎 − 𝑎 + 𝐶𝑀 + 𝑎 + 𝐶𝑀 = 𝑎
Es decir: 𝑞1∗ = 𝑎
𝑞2∗ = 𝑎
Los beneficios serían tal que:
𝜋𝑖 ∗ = 𝑎 + 𝐶𝑀 ∙ 𝑎 − 𝐶𝑀𝑖 ∙ 𝑎 = 𝑎2 + 𝑎 𝐶𝑀 − 𝑎 𝐶𝑀 = 𝑎2
Donde
𝜋1∗ = 𝑎2
𝜋2∗ = 𝑎2
Gráficamente tendríamos:
CR1 (p2)
p2
CR2 (p1)
a+CM
Equilibrio
Bertrand – Nash
a+CM
2
p1
a+CM
2
a+CM
¿Qué sucede si las empresas acuerdan formar un cartel de precios?
Por ejemplo supongamos que acuerdan un cartel de precios en el que doblan los precios:
𝑝𝑖 = 𝑝𝑗 = 2 𝑎 + 𝐶𝑀
y por lo tanto cada una produce 𝑞𝑖 = 𝑎
Entonces los beneficios serían:
𝜋𝑖 𝐶𝐴𝑅𝑇𝐸𝐿 = 2 𝑎 + 𝐶𝑀 ∙ 𝑎 − 𝐶𝑀𝑖 ∙ 𝑎 = 2𝑎2 + 2𝑎 ∙ 𝐶𝑀 − 𝑎 ∙ 𝐶𝑀 = 2𝑎2 + 𝑎 ∙ 𝐶𝑀
𝜋1 𝐶𝐴𝑅𝑇𝐸𝐿 = 𝜋2 𝐶𝐴𝑅𝑇𝐸𝐿 = 2𝑎2 + 𝑎 ∙ 𝐶𝑀
Obviamente esta solución es mejor que la anterior ya que
𝜋𝑖 𝐶𝐴𝑅𝑇𝐸𝐿 = 2𝑎2 + 𝑎 ∙ 𝐶𝑀 > 𝜋𝑖∗ = 𝑎2
Pero ¿existe una mejor situación individual?
CR1 (p2)
p2
CR2 (p1)
a+CM
a+CM
2
p1
a+CM
2
a+CM
Por tanto, en el modelo de Bertrand:
– No existe equilibrio estable
– El proceso reiterativo de bajar el precio continuará hasta que alcance su límite económico natural que es
el coste marginal.
– La solución de precio y cantidad es exactamente idéntica a la de competencia perfecta.
MERCADOS IMPERFECTOS (Stackelberg):
Un mercado con una curva de demanda 𝑋 𝐷 = 100 − 𝑃, el cual es abastecido por dos empresas cuyas
funciones de costes son: 𝐶 𝑥1 = 4𝑥1 y 𝐶 𝑥2 = 2𝑥22 . Determine el equilibrio si la empresa 1 actúa
como líder en precios así como lo siguiente:
a) Curva de oferta de la empresa seguidora
b) Curva de demanda residual de la empresa líder
c) Equilibrio de la empresa líder
d) Cantidad ofrecida por la empresa seguidora
a) Curva de oferta de la empresa seguidora
Consideremos que la Empresa 2 (seguidora) es precio aceptante. Por lo tanto su curva de oferta será tal
que 𝐶𝑀2 ≥ 𝐶𝑀𝑒2
Entonces:
𝐶 𝑥2 = 2𝑥22
=> 𝐶𝑀2 𝑥2 = 4𝑥2
=> 𝐶𝑀𝑒2 𝑥2 = 2𝑥2
4𝑥2 ≥ 2𝑥2
=>
𝑥2 ≥ 0
Pot lo tanto, todo valor positivo sobre la curva de coste marginal es la curva de oferta:
𝑃𝑂 ≡ 𝐶𝑀2 𝑥2 = 4𝑥2
𝑥2𝑂 (𝑃) =
=>
𝑃
4
b) Curva de demanda residual de la empresa líder:
Sabemos que oferta debe igualar a la demanda, por lo tanto:
𝑥1𝐿 + 𝑥2𝑆 (𝑃) = 𝑥 𝐷 𝑃
=>
𝑥1𝐿 = 𝑥 𝐷 𝑃 − 𝑥2𝑆 (𝑃)
=>
𝑥1𝐿 = 100 − 𝑃 − = 100 − 𝑃
𝑃
5
4
4
Por lo tanto la curva de demanda residual para la líder será:
5
𝑋1𝐿 = 100 − 𝑃
4
0
Si 0 ≤ 𝑃 ≤ 80
Si 𝑃 > 80
c) Equilibrio de la empresa líder
𝑀𝑎𝑥.
𝑥1
𝜋 𝑥1 =
400 −4 𝑥 1
5
𝑥1 −
Ingresos
4𝑥1
Costos
C.P.O.
𝛿𝜋
𝛿𝑥 1
=0
𝛿𝜋
𝛿 𝑥1
=
400 −8𝑥 1
5
−4=0
d) Cantidad ofrecida por la empresa seguidora
𝑥2∗ = 10,5
𝑋 ∗ = 100 − 42 = 58
𝜋1∗ = 1805
𝜋2∗ = 220,5
=>
𝑥1∗ = 47,5
𝑃 ∗ = 42
PRACTICAS ADICIONALES
1) Sean dos únicos consumidores, A y B, de quienes se conoce sus preferencias por el bien oro (G) y la
plata (S). Se sabe, que el consumidor A posee inicialmente 3 unidades de oro (G A) y
9 unidades de plata (SA); y que el consumidor B posee inicialmente 8 unidades de oro (GB) y
4 unidades de plata (SB). Con estas dotaciones iniciales, se conoce adicionalmente que la relación
marginal de sustitución (RMSS,G) de plata por oro es de 4 en el caso del consumidor A y de 2 en el
caso del consumidor B.
Se pide:
a) Determine la asignación y los precios de equilibrio general competitivo (EGC) de esta
economía de intercambio puro.
b) ¿Era la dotación inicial eficiente en el sentido de Pareto?
c) Compruebe que la asignación de EGC verifica la Ley de Walras.
2)
Dos empresas 1 y 2, están eligiendo simultáneamente las cantidades 𝑞1 y 𝑞2 , que van a producir de
un producto homogéneo. El costo total de producir 𝑞𝑖 por la empresa 𝑖, 𝑖 = 1,2, es 𝐶𝑇𝑖 = 𝑐 𝑞𝑖 ,
donde 𝑐 > 0 y el precio de equilibrio del mercado, cuando la cantidad agregada en el mercado es
𝑄 = 𝑞1 + 𝑞2 , es tal que 𝑃(𝑄) = 𝑎 − 𝑄, con 𝑄 < 𝑎, 𝑎 > 𝑐. Determine los equilibrios para cada
situación:
i) ¿Qué sucedería si cada firma creyera que es un monopolista?
ii) ¿Qué sucedería si las dos empresas consideran al mismo tiempo la reacción de su rival ante
cambios en las cantidades?
iii) ¿Qué sucedería si las empresas actúan como un cartel en el que se distribuyen a partes iguales la
producción?
iv) Considerando los resultados de los casos ii) y iii), establezca las posibles estrategias de las dos
firmas en este mercado y determine: ¿cuál es el equilibrio de Nash? y ¿Cuál estrategia es Pareto
óptima?
3)
Suponga que existen dos empresas, 1 y 2, que eligen simultáneamente los precios 𝑝1 y 𝑝2 a los que
estarían dispuestos a ofrecer un bien que producen (no diferenciado). Si es conocido por todos que la
demanda de los consumidores es tal que: 𝑞𝑖 𝑝𝑖 , 𝑝𝑗 = 𝑎 – 𝑝𝑖 + 𝑝𝑗 .
i) Determine el equilibrio de Bertrand-Nash de esta situación.
ii) ¿Es este equilibrio eficiente en el sentido de Pareto?.
4)
Dado que en el mercado cada consumidor comprará a la firma que coloque el precio más bajo, las
dos única empresas, 𝑁 = {1,2}, consideran que el único conjunto de estrategias posibles es elegir un
precio tal que 𝑝𝑖 pertenece al conjunto [0 , 𝑎]. Suponiendo que ambas empresas tiene un costo
marginal constante y común dado por 𝑐 > 0 y que la demanda de la i-ésima firma es tal que:
𝑞𝑖 𝑝𝑖 , 𝑝𝑗 =
0
𝑎 − 𝑝𝑖
(𝑎 − 𝑝𝑖 )/2
𝑠𝑖 𝑝𝑖 > 𝑝𝑗
𝑠𝑖 𝑝𝑖 < 𝑝𝑗
𝑠𝑖 𝑝𝑖 = 𝑝𝑗
donde 𝑎 > 𝑐,
i) Encuentre el equilibrio de Bertrand-Nash de esta situación.
ii) Represente gráficamente sus resultados




