ρ ρ ρ ρ ρ ρ

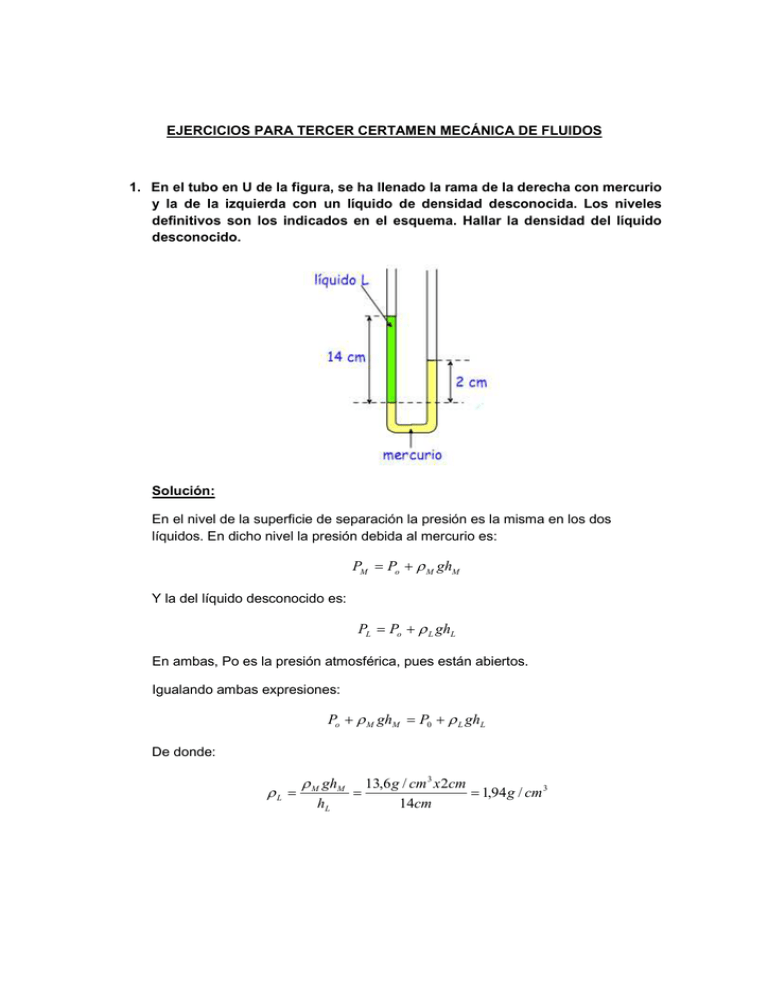
EJERCICIOS PARA TERCER CERTAMEN MECÁNICA DE FLUIDOS
1. En el tubo en U de la figura, se ha llenado la rama de la derecha con mercurio
y la de la izquierda con un líquido de densidad desconocida. Los niveles
definitivos son los indicados en el esquema. Hallar la densidad del líquido
desconocido.
Solución:
En el nivel de la superficie de separación la presión es la misma en los dos
líquidos. En dicho nivel la presión debida al mercurio es:
PM = Po + ρ M ghM
Y la del líquido desconocido es:
PL = Po + ρ L ghL
En ambas, Po es la presión atmosférica, pues están abiertos.
Igualando ambas expresiones:
Po + ρ M ghM = P0 + ρ L ghL
De donde:
ρL =
ρ M ghM
hL
=
13,6 g / cm 3 x 2cm
= 1,94 g / cm 3
14cm
2. Un tanque cilíndrico de 1,80 m de diámetro descansa sobre una plataforma
de una torre a 6 m de altura, como se muestra en la figura. Inicialmente, el
tanque está lleno de agua, hasta la profundidad h0 = 3 m. De un orificio que
está al lado del tanque y en la parte baja del mismo, se quita un tapón que
cierra el área del orificio, de 6 cm2. ¿Con qué velocidad fluye inicialmente el
agua del orificio? ¿Cuánto tiempo necesita el tanque para vaciarse por
completo?
Solución:
Al soltar el tapón, se tiene una situación regulada por la ec de Bernouilli; de tal
manera que se puede calcular la velocidad con que sale inicialmente el agua por el
orificio, como hemos hecho hasta ahora:
P1 +
1 →2
1 →
ρ v 1 + ρgz1 = P2 + ρ v 2 2 + ρgz 2
2
2
Consideraremos la referencia en el piso; además tanto en 1 como en 2 la presión
es la atmosférica, y V1 = 0, puesto que la relación entre las áreas del tanque y del
orificio permite despreciarlo a través de la ecuación de continuidad.
Note que A1/A2 = πr12/6cm2 = 4.239, la velocidad 2 será 4.239 veces mayor que la
velocidad 1.
De lo anterior:
P1 +
1 2
1 →
ρ 0 + ρg ( H + H o ) = P2 + ρ v 2 2 + ρgH
2
2
De donde:
ρg ( H + H o ) − ρgH =
→
1 → 2
ρ v 2 → v 2 2 = 2 gH o
2
Por lo tanto:
→
v 2 = 2 x9,8m / s 2 x3m = 7,7m / s 2
Luego, aplicando nuevamente Bernouilli para los puntos 2 y 3, se puede calcular la
velocidad con que llega el agua al suelo:
P2 +
1 → 2
1 →
ρ v 2 + ρgh2 = P3 + ρ v 3 2 + ρgh3
2
2
P0 +
1 → 2
1 →
ρ v 2 + ρgH = P0 + ρ v 3 2 + ρg 0
2
2
Con P2 = P3 = PO
De donde:
→
→
v 3 = v 2 + 2 gH
2
2
→
v 3 = 58,8m / s 2 + 2 x9,8m / s 2 x6m = 13,3m / s 2
Hasta aquí, el problema es resuelto como ha predicho la teoría expuesta. Sin
embargo, calcular el tiempo que demora el tanque en vaciarse requiere de
consideraciones distintas, puesto que la profundidad no será constante, como en
otros casos. Esto producirá que la velocidad con que baja el fluido en el tanque,
así como la velocidad con que sale el líquido por el orificio, no sean constantes en
el tiempo.
Para resolver esto, se considerará que la altura h del líquido disminuye en dh
durante un intervalo de tiempo dt (ver figura). Entonces, la velocidad con que baja
el fluido en el tanque V1, queda determinada por la expresión:
→
v1 = −
dh
dt
Negativa, puesto que h disminuye con el tiempo.
Adicionalmente se tiene que:
A1v1 = A2 v 2
Expresión que es cierta para todo t, de donde:
v1 = v 2
A2
A1
Al igualar ambas expresiones, se tiene:
A
dh
= v2 2
dt
A1
−
Y con Torricelli:
→
v 2 = 2 gh
Por lo que:
−
A
dh
= 2 gh 2
dt
A1
Que se puede expresar como:
−
dh
h
= 2g
A2
dt
A1
Integrando la expresión para el intervalo entre t = 0, donde la profundidad es h0 y
el tiempo t = t, donde la profundidad es h, se tiene:
−∫h
−1
2
dh = 2 g
A2
dt
A1 ∫
Integrando:
1
1
A
− 2 h 2 − h0 2  = 2 g 2 t


A1
Despejando t:
1
1
− 2 A1  h 2 − h0 2 


t=
2 g A2
Cuando el tanque se vacié, h = 0 por lo que:
t=
(
− 2 A1 − h0
2 g A2
1
2
) = − 2πr (− h ) = − 2 x3,14 x0,9m x3m
1
2
1
2 g A2
0
2
2
1
2
2 x9,8m / s 2 x0,006m 2
= 3.623,6seg
3. Por una tubería horizontal de 20 mm de diámetro, circula un fluido con una
velocidad de 3 m/s.
a) Calcular el caudal en L/min.
b) Calcular la velocidad en otra sección de la misma línea de 10 mm de
diámetro.
c) Si el fluido es agua, calcular la diferencia de alturas entre dos tubos
verticales colocados inmediatamente antes y después del
estrechamiento. Considere la densidad del agua como 1g/cm3.
Solución:
a)
b)
c)
4. Un cilindro vertical de vidrio tiene un diámetro interior de 150 mm y un
agujero taladrado cerca de la base. Se mantiene un nivel constante de agua
de 350 mm por encima del agujero del que sale horizontalmente hacia el
exterior un chorro de 5 mm de diámetro. ¿Cuál es la velocidad del agua a la
salida del chorro?
Solución:
5. Una bomba aspirante está instalada en un pozo de 6 m sobre el nivel del
agua y tiene las siguientes características. Calcule:
Diámetro del émbolo: 12 cm.
Carrera del émbolo: 30 cm.
Cadencia: 30 emboladas por minuto.
a) El caudal
b) La potencia absorbida por el motor, suponiendo un rendimiento η = 0,6.
Solución:
a)
b)
6. Por la tubería horizontal representada en la figura circula agua. El diámetro
de las secciones 1 y 3 es Ø = 20 cm, reduciéndose en la sección 2 a la mitad.
Considere g = 10m/s2.
a) Ordenar presiones y velocidades en los puntos 1, 2,3 de mayor a menor.
b) Calcular el caudal, expresado en litros por segundo, si la diferencia de
presiones entre ambas secciones es 0,3 kp/cm2.
Solución:
a) Considerando el agua como un fluido ideal, se cumple: P1 = P3 > P2 y v1 = v3 < v2.
b)
7. Calcule la fuerza de un cilindro de doble efecto, tanto en el avance como en
el retroceso, que tiene las siguientes características:
Diámetro del cilindro: 80 mm
Diámetro del vástago: 25 mm
Presión de trabajo: 6 kgf/cm2
Fuerza de rozamiento: 10% de la fuerza teórica
Solución:
8. Un cilindro hidráulico tiene un diámetro de 100 mm y un vástago de 60 mm
de diámetro. Sabiendo que la presión de trabajo es de 315 kg/cm2 y que las
pérdidas por rozamiento son del 12%, calcule la fuerza de tracción y de
compresión.
Solución: