cálculo del coeficiente de amortiguamiento, , de un

Laboratorio de Física
PRÁCTICA REMOTA
PÉNDULO FÍSICO AMORTIGUADO
1. OBJETIVO
Estudio del comportamiento de un péndulo físico débilmente amortiguado.
Determinación de la constante de amortiguamiento, γ, del periodo, T, de la frecuencia
angular del movimiento, ω, y de la velocidad angular instantánea, θ .
2.- FUNDAMENTO TEÓRICO
Se denomina péndulo físico a cualquier sólido rígido capaz de oscilar en torno a un
eje horizontal.
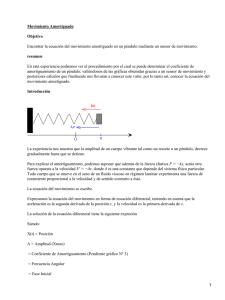
En la figura 1 se muestra un péndulo físico que puede girar verticalmente en torno a
un eje horizontal que pasa por el punto O. En la posición de equilibrio el Centro de Masas
(C. M) está situado en la vertical que pasa por O; cuando se gira un ángulo θ con respecto
al equilibrio como aparece en la figura, el peso (mg) y un momento de amortiguamiento
(γvD), junto con la reacción (R) en el punto de apoyo (barra horizontal) forman pares de
fuerzas que provocarán un giro en torno al eje que generará un movimiento oscilatorio.
Figura 1.- Péndulo Físico
La ecuación del movimiento del péndulo se puede deducir a partir de la expresión:
ΣMO=IOα ⇒ mg L senθ+γv D=-IOα
donde, α =
d 2θ
dt 2
y
v=
D dθ
2 dt
⇒
d 2 θ γD 2 dθ mgL
senθ = 0
+
+
IO
dt 2 2I O dt
(1)
(2)
Página 1 de 5
Laboratorio de Física
siendo “IO” el Momento de Inercia respecto al eje de rotación, “D” el diámetro del eje y
“γ” la constante de amortiguamiento.
La ecuación (2) no tiene una solución sencilla a menos que se haga la aproximación:
senθ≅θ, tanto más correcta cuanto más pequeñas sean las oscilaciones.
En tal situación, la ecuación del movimiento quedará expresada como:
d 2θ
dθ
+ 2β + ω02θ = 0
2
dt
dt
(3)
Siendo ωo la frecuencia natural de oscilación y β el parámetro de amortiguamiento.
ω0 =
mgL
γD 2
y β=
4IO
IO
La solución a la ecuación diferencial va a tener una componente que nos define el
amortiguamiento, (θ 0 e −βt ) , y una componente que nos indica que el movimiento es
periódico (sen ωt):
(4)
θ = θ 0 e −βt sen ( ωt )
siendo “θ0” la amplitud inicial y “ω" la frecuencia del movimiento, ω = ω 0 1 −
β2
ω 02
Como se puede observar en la figura 2, el movimiento es oscilatorio amortiguado,
con la amplitud disminuyendo a medida que avanza el tiempo.
0,6
Angular Position (rad)
0,4
0,2
0,0
-0,2
-0,4
-0,6
0
1
2
3
4
5
6
Time (s)
Figura 2.- Oscilaciones amortiguadas
Página 2 de 5
Laboratorio de Física
3.- EXPERIMENTACIÓN
La práctica a realizar consiste en el estudio de las oscilaciones de una barra
rectangular, que jugará el papel de péndulo físico. Para ello se separará la regla un ángulo θ0
de su posición de equilibrio dejándola a continuación en libertad.
El sistema dispone de un sensor de rotación con el que se medirá el ángulo en
función del tiempo, θ(t).
Entre en la página Web del departamento http://goya.eis.uva.es, elija la opción
“Laboratorio Remoto” y seleccione la aplicación “Péndulo Físico Amortiguado”. Introduzca el
nombre de usuario y la contraseña que les han facilitado.
Lea con detenimiento la página de bienvenida y seleccione en el menú de la
izquierda de la página la opción “Péndulo Real”. Entrará así en una nueva ventana en la que
podrá realizar la experiencia.
Pulse en la flecha,
, situada en la esquina izquierda del registro, introduzca el valor
del ángulo desde donde el péndulo va a oscilar (utilicen sólo ángulos menores de 50o) y
pulse “Iniciar”. En este momento el sistema comenzará la adquisición de datos a la vez que
el péndulo se va desplazando hasta alcanzar el valor del ángulo que se le ha indicado, para
seguidamente ser liberado comenzando las oscilaciones.
Una vez que el péndulo haya cesado su movimiento pulsen “Parar” para que el
sistema deje de registrar datos. Para realizar posteriormente el análisis del movimiento será
necesario que en el experimento se hayan registrado como mínimo 5 oscilaciones.
Si desea repetir de nuevo el experimento siga los pasos indicados en los párrafos
anteriores.
En la esquina superior derecha de la página se puede acceder a los resultados (los
datos registrados son la posición angular (rad) y el tiempo (s)). Guarde estos datos en un
fichero con extensión *.txt.
Abra este fichero en una Hoja de Cálculo (ej. Excel), importando los datos a partir
del fichero anterior y realice la representación Posición Angular = f (Tiempo). Obtendrá
el mismo gráfico que visualizaron in situ al realizar la experiencia.
Debe tener en cuenta la siguiente indicación: el tiempo comienza a registrarse en
cuanto el péndulo se pone en movimiento para alcanzar el ángulo que se le ha indicado.
Pero el tiempo real que debe utilizar es el que se registra cuando el péndulo se libera,
cumpliéndose en ese momento θ ( t = 0 ) = θ o . Es decir, se deben eliminar aquellos datos
anteriores a la situación de posición angular máxima, y se deben sustraer a los tiempos el
dato del tiempo correspondiente a dicha posición.
3.1 Cálculo de la constante de amortiguamiento, γ.
Para el cálculo de la constante de amortiguamiento se tendrá en cuenta
dependencia exponencial de la amplitud en función del tiempo, es decir:
la
Página 3 de 5
Laboratorio de Física
Θ = θ 0 e −βt = θ o e
−
γD 2
t
4 IO
(5)
siendo Θ el valor de la amplitud (posición máxima o mínima) en cada periodo de oscilación
(ver figura 3).
Figura 3.- Valores de las Amplitudes máximas para cada Periodo de oscilación
Será pues necesario obtener los valores de Θ y los correspondientes de t. Si se utiliza
la hoja de cálculo Excel esto puede hacerse fácilmente, ya que representando los datos
experimentales θ=f(t), al situar el cursor en un punto se obtienen directamente sus
coordenadas {x,y} (en este caso, {t, θ}).
Si se toman logaritmos neperianos en la expresión (5), obtendremos:
ln Θ = ln θ o −
γD 2
t
4I O
(6)
Esto indica que lnΘ es linealmente proporcional al tiempo (t), con una constante de
γD 2
proporcionalidad igual a −
(que es justamente la pendiente de la recta lnΘ = f(t) y
4I O
cuyo valor absoluto coincide con β ).
Así, al representar lnΘ = f(t) se debe obtener una línea recta. Realizando un ajuste
por mínimos cuadrados a la función, del valor de la pendiente se podrá obtener la
constante de amortiguamiento, γ. (Este coeficiente deberá tener el mismo valor tanto si se
trabaja con los puntos de amplitud máxima en coordenadas positivas como si se trabaja
con los puntos de amplitud máxima en coordenadas negativas).
Página 4 de 5
Laboratorio de Física
3.2 Cálculo de la frecuencia de vibración, ω.
El valor de la frecuencia de vibración se puede conocer a partir de la medida directa
del periodo, T, en la representación θ=f(t)
ω=
2π
T
(7)
A partir de los valores calculados “γ” y “ω” y de la amplitud inicial “θo”, utilizando la
ecuación del movimiento (4) y dando diferentes valores a t (tiempo), obtengan los valores
correspondientes a las diferentes amplitudes.
Representen conjuntamente los datos experimentales, θ=f(t), y los obtenidos a
partir de los valores calculados . Discutan si existen diferencias significativas entre ambos.
3.3 Cálculo de la velocidad angular instantánea
Para calcular la velocidad angular instantánea y con objeto de minimizar los errores
experimentales se procederá como se describe a continuación. Utilizando únicamente 1 de
cada 10 valores experimentales (θo,t), (θ10, t), (θ20,t),…. Se calculará la diferencia entre los
valores consecutivos de las posiciones y de los tiempos θ10(n+1)-θ10n y t10(n+1)-t10n, con n = 0,
1, 2,…para obtener la velocidad como:
.
θ=
∆θ
∆t
(8)
Representen la posición en función de la velocidad angular, θ=f( θ ). Analicen y
discutan la forma de la gráfica, relacionándola con el hecho de estar estudiando un
movimiento amortiguado.
Datos: considere el péndulo como una barra rectangular de masa, m= 40.4 g y
dimensiones las de la figura, siendo el espesor despreciable y la distancia entre los orificios
de 9 mm.
Diámetro del eje: D=6.5 mm
Página 5 de 5