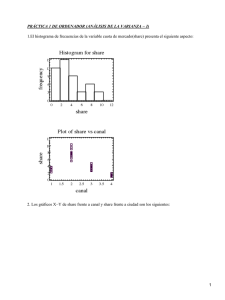
l_Capitulo 8_Pruebas estadísticas
Anuncio

Capitulo 8. Pruebas estadísticas 8.1 Introducción Existen pruebas estadísticas que por lo general son utilizadas para verificar la homogeneidad de las varianzas y comparar pares de medias. El test de Bonferroni, los test estadísticos de igualdad de varianza, la comparación entre medias, los métodos de comparación de pares de media de tratamientos, así, el test de Tukey, el test de T de Student, el test de la amplitud Múltiple de Duncan y el análisis de varianza son los más usados en el análisis de experimentos. 8.2 Método de Bonferroni El modelo para el estudio del análisis de varianza con un único factor es dado por: (8.1) Se sabe que los estimadores de la media y de los efectos de los tratamientos son dados por: (8.2) (8.3) Y el intervalo de confianza para la media del i-ésimo tratamiento es dado por: (8.4) El intervalo de confianza para la diferencia entre las medias de dos tratamientos, es dado por: (8.5) Los intervalos de confianza, expresados por las ecuaciones (8.4) y (8.5) son intervalos considerados como uno de cada vez. O sea, el nivel de confianza, una estimativa en particular. 70 , se aplica solamente a Muchas veces, es esta interesado en determinar confianza. La probabilidad de que intervalos de interés, con de intervalos estén simultáneamente correctos es en el mínimo . La probabilidad frecuentemente es llamada de coeficiente global de confianza. Eso implica que a medida que aumenta, el nivel de confianza del conjunto de intervalos de confianza disminuye. Con la finalidad de contornear ese problema, en vez de usar (8.4) y (8.5), debe usarse en las ecuaciones . Ese procedimiento es conocido como el método de Bonferroni, permitiendo al experimentalista construir un conjunto de intervalos simultáneos de confianza para las medias de los tratamientos o para la diferencia entre las medias de los tratamientos para los cuales el nivel global de confianza es en lo mínimo Al final de cualquier planeamiento, se precisa verificar la adecuación del modelo matemático obtenido y la validad de las suposiciones hechas. 8.3 Test estadísticos para la igualdad de la varianza Aunque la desigualdad de varianza puede ser evaluada por el análisis de los gráficos de los residuos, existen pruebas estadísticas que son más precisos. Una prueba bastante usada es la prueba de Bartlett. El test calculará una estadística, cuya distribución de la muestra es bien aproximada por la distribución libertad, cuando las , con ( ) grados de muestras aleatorias fueran provenientes de poblaciones normales independientes. La estadística de prueba es dada por: (8.6) Donde: (8.7) (8.8) 71 (8.9) Siendo, la varianza de la muestra de la i-esima población. La cantidad cuando las varianzas muéstrales fueran iguales. Así, rechazamos rechazaremos distribución difieren mucho; siendo igual a cero cuando todas las si los valores de solamente si , con es grande ; siendo fueran muy grandes; o sea, el punto porcentual superior de la grados de libertad. El inconveniente de la prueba de Bartlett es el hecho de ser muy sensible a la suposición de la normalidad. Luego de existir alguna duda con relación a esa suposición, el test no debe ser usado. Existen otros test estadísticos para la igualdad de varianza, tal como el test modificado de Levene, que es un procedimiento muy bueno y robusto cuando hay desvíos en la normalidad. El test usa el desvío absoluto de las observaciones del tratamiento, en cada tratamiento en relación a la mediana . Los desvíos son dados por: (8.10) La prueba modificada de Levene evalúa si la media de esos desvíos son o no iguales para todos los tratamientos. Si los desvíos medios fueran iguales, las varianzas de las observaciones en todos los tratamientos serán las mismas. La estadística de prueba usada en el test de Levene es una usual estadística F, usada para testar la igualdad de medias, aplicada a los desvíos absolutos. 8.4 Comparaciones entre medias Lo que se ha presentado en los puntos anteriores, en el análisis de varianza, es determinar si hay globalmente diferencia entre las medias de los tratamientos. Eso quiere decir que no se sabe exactamente que media difiere. Los procedimientos usados para comparar grupos de medias o medias individuales es el llamado de métodos de comparación múltiple. 72 8.4.1 Métodos gráficos de comparación Las medias de la resistencia pueden ser colocadas en una línea para cada valor del tenor de algodón, conforme mostrado en la Fig. 8.1, analizando esa figura, se tiene una idea cualitativa de que medias tienen o no valores aproximadamente iguales. Figura 8.1 Medias de las resistencias, como una función del tenor de algodón (Montgomery, 2001) 8.4.2 Contrastes Como se observa, existen diferencias entre las medias de los tratamientos, pero no se sabe exactamente entre cuales ocurre esa estadística. Imaginemos que se quiera mostrar que no existe diferencia entre los tratamientos 4 y 5; o sea: (8.11) O también: (8.12) Y que la media de los niveles más bajos no difiera de la media de los niveles superiores: (8.13) O también: (8.14) En general, un contraste es una combinación lineal de parámetros de la forma: 73 (8.15) Donde las constantes, ,…. de los contrastes deben sumar cero, esto es: 0, de esta forma, las hipótesis anteriores pueden ser expresadas como: (8.16) (8.17) Las constantes para la ecuación (8.16) son: constantes para la ecuación (8.17) ; y ; y las . La prueba de hipótesis envolviendo contrastes puede ser hecho de dos maneras básicas. El primer método usa el test t. Escriba el contraste de interés en términos de los totales de los tratamientos: (8.18) La varianza de es cuando los tamaños de las muestras en cada tratamiento son iguales. Si la hipótesis nula en la ecuación (8.16) fuera verdadera, la razón: (8.19) Tendrá una distribución N(0,1) como la varianza su estimativa, la media cuadrática del error: es generalmente desconocida, se usa resultando en la estadística de prueba: (8.20) La hipótesis nula, será entonces rechazada si 74 La segunda manera usa el test F. el cuadrado de una variable aleatoria , con libertad, es una variable aleatoria F, con grados de libertad iguales a 1 y grados de , para el numerador y el denominador respectivamente, así: (8.21) La hipótesis nula será rechazada si ; otra forma de escribir la ecuac. (8.21) (8.22) (8.23) En el caso de tratamientos con diferentes tamaños de muestra, los siguientes cambios deben ser hechos: (8.24) (8.25) (8.26) 8.4.3 Métodos para la comparación de pares de medias de tratamientos La idea ahora es comparar todos los pares de medias de tratamientos, resultando las siguientes hipótesis: ; ; Para todo Las pruebas que serán presentadas aquí, son utilizados después que, a través de un análisis de varianza, fuera verificada la existencia de una diferencia global entre los tratamientos. 75 8.4.3.1 Test de Tukey Tukey (1953) propuso un procedimiento para testar la hipótesis nula, con siendo exactamente el nivel global de significancia, cuando las muestras tienen tamaños iguales, y en el máximo , cuando las muestras tienen tamaños diferentes. El test de Tukey utiliza la distribución de la estadística de amplitud en la forma de Student (8.27) Siendo: , la mayor y menor media respectivamente. (8.28) Siendo : el numero de grados de libertad, asociado con ,y se halla en las tablas estadísticas. Si el valor absoluto de la diferencia entre dos medias fuera mayor de entonces debe ser rechazada. Para muestras con tamaños diferentes, la ecuación (8.28) es modificada para: (8.29) La versión para muestras de tamaños diferentes es a veces llamada de procedimiento de TukeyKramer. 8.4.3.2 Método de la mínima diferencia significativa (LSD) de Fisher La estadística de prueba para la hipótesis: es: (8.30) 76 Un par de medias será estadísticamente diferente, si: (8.31) Si las muestras tuvieran el mismo tamaño; entonces: (8.32) Note que el riesgo global , puede ser considerablemente aumentado usando este método. Específicamente en la medida que aumenta, el error tipo I, del experimento entre el número de experimentos en el cual un error de tipo I es hecho y el número total de experimentos se torna grande. 8.4.3.3 Test de la amplitud múltiple de Duncan El test, desarrollado por Duncan (1955) es largamente utilizado para comparar pares de medias. Para el test de Duncan, las medias de los tratamientos (con el mismo tamaño de muestras) son colocadas en orden creciente y el error estándar de cada media es determinado por: (8.33) En el caso de muestras con tamaño diferentes, de las debe ser cambiado por la media harmónica, , , quedando con: (8.34) En las tablas estadísticas, se presentan los valores de las amplitudes . En el que es el nivel de significancia y asociado a la media cuadrática del error . 77 para es el número de grados de libertad Un conjunto de amplitudes de mínima significancia deber ser obtenido, a través de: (8.35) Las diferencias observadas entre las medias son probadas, comenzando con la mayor versus la menor y luego entonces comparadas con . A seguir, una nueva diferencia entre las medias es calculada, comenzando con la próxima mayor versus la próxima menor, y entonces comparada con . El proceso continua hasta el final. Si una diferencia observada fuera mayor que la correspondiente amplitud de mínima significancia, , se concluye que el par de medias en cuestión es estadísticamente diferente. Para evitar contradicción, ninguna diferencia entre un par de medias será considerada significante, si esas dos medias envolvidas estuvieran entre dos medias que no difieran significativamente. El test de Duncan es muy efectivo en detectar diferencias entre medias, cuando diferencias reales existen. Esa es la razón por la cual el test referido es bastante popular. 8.4.3.4 Métodos para la comparación de pares de medias de tratamiento El modulo ANOVA de Statistica realiza todas estas pruebas de hipótesis a respecto de la igualdad de medias de los tratamientos. Supongamos que se desea unificar el efecto porcentual de algodón en la resistencia de un tejido, los siguientes datos experimentales fueron recogidos y colocados en una planilla que se presenta en la tabla 8.1. 78 Tabla 8.1 Base de datos del porcentaje de algodón en la resistencia de un tejido concentracion(%) resistencia 15 7 15 7 15 15 15 11 15 9 20 12 20 17 20 12 20 18 20 18 25 14 25 18 25 18 25 19 25 19 30 19 30 25 30 22 30 19 30 23 35 7 35 10 35 11 35 15 35 11 Fuente: Montgomery (2001) Accione el modulo del ANOVA del programa de Statistica, obteniendo la siguiente ventana tal como se presenta en la Fig. 8.1 Figura 8.1 Ventana del análisis de ANOVA Seleccione la opción One-way ANOVA, visto que solo existe un factor para ser analizado. Luego presione OK y si se seleccionará las variables, la siguiente ventana surgirá, tal como se presenta en la Fig.8.2. 79 Figura 8.2 Ventana para seleccionar All efects El análisis de varianza es obtenida rápidamente al seleccionarse la opción All effects, resultando en la Fig.8.3. Figura 8.3 Ventana del resultado del análisis de varianza Esa misma diferencia, con la barra de error, puede ser vista en forma grafica, escogiéndose la opción. All effects/graphs y presionándose OK. Resultando en la Fig.8.4 80 "Var1"; LS Means Current effect: F(4, 20)=14,757, p=,00001 Effective hypothesis decomposition Vertical bars denote 0,95 confidence intervals 26 24 22 Resistencia 20 18 16 14 12 10 8 6 4 15 20 25 30 35 Porcentaj e de algodon(%) Figura 8.4 Influencia del porcentaje de algodón sobre la resistencia del tejido La media cuadrada del error (Fig.8.3) es 8,06. El test F muestra que hay una diferencia estadísticamente significativa entre los tratamientos. No se sabe por en cuanto, donde esta esa diferencia. Se usan, entonces los test, ya referidos, seleccionándose la opción More results, se obtiene la siguiente ventana, tal como se muestra en la Fig. 8.5; Figura 8.5 Ventana de Anova 81 Las pruebas que se necesitan hacer se encuentran en la pasta Post-hoc que al ser seleccionada, resulta en la Fig.8.6: Figura 8.6 Ventana de ANOVA A partir de aquí, se selecciona el factor que se quiere analizar y presionando el test deseado, resultando una serie de ventanas dadas a continuación, cada una siendo referente a un método, tal como mostrado los resultados en las Figuras 8.7, 8.8, 8.9 y 8.10 Figura 8.7 Ventana del resultado con el método de Fisher LSD Figura 8.8 Ventana del resultado con el método de Bonferroni 82 Figura 8.9 Ventana del resultado con el método de Scheffe Figura 8.10 Ventana del resultado con el método de Tukey Como visto anteriormente, no solo existe diferencia entre las medias de los tratamientos 2y3 y 1y5. El método de Scheffé presenta menos diferencias significativas que los demás métodos. Estos métodos son validos si la varianza se muestra homogénea. Entonces las pruebas vistas anteriormente deben ser hechas a fin de verificar si esa suposición está siendo atendida para esos datos. El programa de Statistica, realiza esas pruebas y se selecciona la pasta Assumptions, resultado en: las pruebas de Cochran, Hartley, Bartlett y Levene resultan en las ventanas dadas a continuación y presentadas en las figuras 8.11 y 8.12 respectivamente. Como el valor p fue mayor que 0,05; la hipótesis de homogeneidad es aceptada. 83 Figura 8.11 Ventana del test de Hartley, Cochran y Bartlett de homogeneidad de varianza Figura 8.12 Ventana del test de Leven de homogeneidad de varianza Otro grafico importante es aquel que relaciona la desviación estándar (o varianza) con las medias de los tratamientos. No puede haber cualquier correlación entre esas dos variables. El grafico puede ser hecho en Statistica, si al seleccionar la opción Plot means vs Std, deviations. Por la Fig 8.13, se percibe que no hay correlación entre la desviación estándar y la media de los tratamientos. Means vs. Std.Dvs: Var2 Effect: "Var1" 3,4 3,2 Standard Deviations 3,0 2,8 2,6 2,4 2,2 2,0 8 10 12 14 16 18 20 22 24 Means Figura 8.13 Relación entre los desvíos estándares y las medias 84