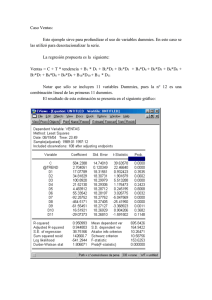
Sobre la distribución nula exacta del estadístico de Wald para p=p0
Anuncio

Sobre la distribución nula exacta de Wald, Score y TRV para contrastar p=p0
>
>
>
>
>
p0 <- 0.15 ### Hipótesis nula p=p0
n <- 13 ### total
y <- 5 ### éxitos observados
phat <- y/n ### valor estimado de p
se.phat <- sqrt(phat*(1-phat)/n)
> ### logverosimilitud de p
> logver <- function(p){ y*log(p)+(n-y)*log(1-p) }
>
>
>
>
### Estadísticos Wald, Score y TRV para contrastar p=p0 ###
Wald.p0 <- ( (phat - p0)^2 ) * (n / (phat * (1-phat)) )
Score.p0 <- ( (phat - p0)^2 ) * (n / (p0 * (1-p0)) )
TRV.p0 <- 2*( logver(phat) - logver(p0) )
>
>
>
>
### p-valor asintótico de los tests Wald, Score y TRV ###
pv.Wald.p0 <- 1 - pchisq(Wald.p0, 1)
pv.Score.p0 <- 1 - pchisq(Score.p0, 1)
pv.TRV.p0 <- 1 - pchisq(TRV.p0, 1)
> round(cbind( n, y, phat, se.phat, p0 ), 4)
n y
phat se.phat
p0
[1,] 13 5 0.3846 0.1349 0.15
> round(cbind( Wald.p0, pv.Wald.p0, Score.p0, pv.Score.p0, TRV.p0, pv.TRV.p0), 4)
[1,]
Wald.p0 pv.Wald.p0 Score.p0 pv.Score.p0 TRV.p0 pv.TRV.p0
3.0233
0.0821
5.6124
0.0178 4.2483
0.0393
> #####################################################
> x <- c(0:n) ### posibles éxitos en n ensayos
> px <- x/n ### posibles valores que toma el estimador de p
> prob <- dbinom(x, n, p0) ### probabilidades binomiales bajo p0
> ### logverosimilitud
> logver2 <- function(px,p){ n*px*log(p)+(n*(1-px))*log(1-p) }
>
>
>
>
### funciones que calculan los valores de Wald, Score y TRV ###
f.wald.p0 <- function(px) {( (px - p0)^2 ) * (n / (px * (1-px)) )}
f.score.p0 <- function(px) {( (px - p0)^2 ) * (n / (p0 * (1-p0)) )}
f.trv.p0 <- function(px) { 2*( logver2(px,px) - logver2(px,p0) ) }
>
>
>
>
>
wald <- f.wald.p0( px ) ### valores del estadístico de WALD para p0
score <- f.score.p0( px ) ### valores del estadístico Score para p0
trv <- f.trv.p0( px )
trv[x==0] <- Inf
### corrección para evitar NaN
trv[x==max(x)] <- Inf
>
>
>
>
### p-valor exacto de los tests Wald, Score y TRV
pv.wald.exact <- sum(prob[wald >= Wald.p0])
pv.score.exact <- sum(prob[score >= Score.p0])
pv.trv.exact <- sum(prob[trv >= TRV.p0])
> round(cbind(Wald.p0, pv.Wald.p0, pv.wald.exact), 4)
[1,]
Wald.p0 pv.Wald.p0 pv.wald.exact
3.0233
0.0821
0.1551
1
> round(cbind(Score.p0, pv.Score.p0, pv.score.exact), 4)
[1,]
Score.p0 pv.Score.p0 pv.score.exact
5.6124
0.0178
0.0342
> round(cbind(TRV.p0, pv.TRV.p0, pv.trv.exact), 4)
TRV.p0 pv.TRV.p0 pv.trv.exact
[1,] 4.2483
0.0393
0.1551
>
>
>
>
>
>
>
### Otro test exacto basado en la diferencia observada: abs(px-p0) ###
### todos los valores del estadístico diferencia observada respecto de p0
dif.px.p0 <- abs( px-p0 )
### valor observado del estadístico
dif.obs <- abs(phat-p0)
### pvalor exacto
pv.dif.obs <- sum(prob[dif.px.p0 >= dif.obs])
> round(cbind(dif.obs, pv.dif.obs), 4)
[1,]
dif.obs pv.dif.obs
0.2346
0.0342
> round(cbind(x, px, wald, score, trv, dif.px.p0, prob), 4)
[1,]
[2,]
[3,]
[4,]
[5,]
[6,]
[7,]
[8,]
[9,]
[10,]
[11,]
[12,]
[13,]
[14,]
x
0
1
2
3
4
5
6
7
8
9
10
11
12
13
px
wald
score
0.0000
Inf 2.2941
0.0769
0.9777 0.5445
0.1538
0.0015 0.0015
0.2308
0.4778 0.6652
0.3077
1.5176 2.5354
0.3846
3.0233 5.6124
0.4615
5.0770 9.8959
0.5385
7.8936 15.3861
0.6154 11.8958 22.0830
0.6923 17.9481 29.9864
0.7692 28.0811 39.0965
0.8462 48.3969 49.4133
0.9231 109.4194 60.9367
1.0000
Inf 73.6667
trv dif.px.p0
prob
Inf
0.1500 0.1209
0.6438
0.0731 0.2774
0.0015
0.0038 0.2937
0.5878
0.0808 0.1900
2.0540
0.1577 0.0838
4.2483
0.2346 0.0266
7.0959
0.3115 0.0063
10.5651
0.3885 0.0011
14.6559
0.4654 0.0001
19.4000
0.5423 0.0000
24.8722
0.6192 0.0000
31.2243
0.6962 0.0000
38.8050
0.7731 0.0000
Inf
0.8500 0.0000
Las columnas wald, score y trv contienen los diferentes valores que pueden tomar los
estadísticos Wald, Score y TRV respectivamente, para contrastar p=p0 (p0=0.15).
La columna dif.px.p0, contiene los valores de las diferencias abs(px-p0).
La última columna, prob, contiene las probabilidades binomiales de una b(n, p0).
Se puede observar que la distribución exacta bajo p0 de los estadísticos de WALD y TRV,
asignan probabilidad positiva (prob[1] + prob[14] = 0.1209055) a un valor infinito. Por ello
el p-valor exacto resulta ser tal elevado, al añadir en este caso el valor prob[1] (0.120955) al
p-valor obtenido en los otros dos tests.
También se ve que los valores tan extremos o más que el observado, tanto en el test Score
como en el test diferencia absoluta, tienen idéntica probabilidad, lo que hace que el p-valor
exacto sea 0.034 (diferente del p-valor asintótico del test Score).
2